35. Формула Кронекера Капелли.
Система
линейных уравнений совместна тогда и
только тогда, когда ранги матриц A
и 
совпадают,
т.е.
r(A) = r(
)
= r.
Для множества М решений системы (5.1) имеются три возможности:
1) M = ∅ (в этом случае система несовместна);
2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);
3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.
Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (m≥n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2, (5.3)
... ... ... ... ... ...
an1 x1 + an1 x2 +... + ann xn = bn.
Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом.
Доказательство (условия совместности системы)
Необходимость
Пусть
система
совместна. Тогда существуют числа
такие,
что
.
Следовательно, столбец
является
линейной комбинацией столбцов
матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что
.
Достаточность
Пусть
.
Возьмем в матрице
какой-нибудь
базисный минор. Так как
,
то он же и будет базисным минором и
матрицы
.
Тогда согласно теореме о базисном миноре
последний столбец матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
36.Условия определенности и неопределенности систем линейных уравнений.
Теорема: Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой
Теорема: Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.
37.Решение систем линейных уравнений методом Гаусса.
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме.Для того чтобы решить систему уравнений
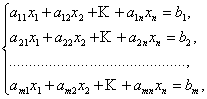выписывают
расширенную матрицу этой системы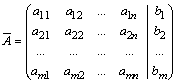 
и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы 
будут
располагаться нули.
Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы.