32.Система линейных уравнений и ее решение. Различные формы записи системных уравнений. Определение однородной, неоднородной, совместной, несовместной, определенной и неопределенной системы.
Линейным
уравнением (или уравнением первого
порядка) с n неизвестными x1; x2; ... xn
называется уравнение вида
Величины a1; a2;...; an называются коэффициентами при неизвестных, а
b — свободным членом уравнения (1). Коэффициенты при неизвестных и
свободный член предполагаются известными.
Векторная форма записи
Система уравнений может быть записана в векторном виде:
A1x1 + A2x2 + ... + Anxn =B
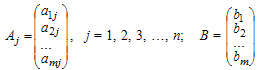
Матричная форма записи
В матричной записи система линейных уравнений может быть записана следующим образом:
AX=B
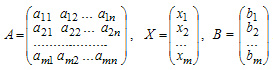
Решением системы уравнений называется такой n-мерный вектор Х = (x1, x2,...,xn), который одновременно является решением каждого из уравнений системы.
Системы уравнений бывают:
Если все свободные члены системы линейных уравнений равны 0, то система называется однородной, в противном случае — неоднородной (Если
,
то система линейных алгебраических
уравнений называется однородной, в
противном случае – неоднородной.)
Равносильными называются две системы уравнений, если они имеют одно и тоже множество решений
Совместной называется система уравнений, если она имеет хотя бы одно решение.
Несовместной называется система уравнений, если она не имеет ни одного решения.
Определенной называется система уравнений, если она имеет единственное решение.
Неопределенной называется система уравнений, если она имеет бесконечное множество решений.
33.Матричный способ решения систем линейных уравнений.
Пусть
для матрицы А порядка n на n существует
обратная матрица 
.
Умножим обе части матричного
уравнения 
слева
на
(порядки
матриц A ⋅ X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем 
.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как 
,
а по определению обратной матрицы 
(E–
единичная матрица порядка n на n),
поэтому
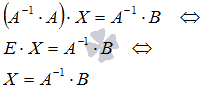Таким
образом, решение системы линейных
алгебраических уравнений по матричному
методу определяется равенством 
.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы
.
Мы
знаем, что квадратная
матрица А порядка n на n имеет
обратную матрицу
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ.
34.Формулы Крамера.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А и n вспомогательных определителей i , которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
Рассмотрим
систему уравнений 
На
первом шаге вычислим определитель 
,
его называют главным
определителем системы.
Если 
,
то система имеет бесконечно много
решений или несовместна (не имеет
решений). В этом случае правило Крамера
не поможет, нужно использовать метод
Гаусса.
Если 
,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя:
и 
На
практике вышеуказанные определители
также могут обозначаться латинской
буквой 
.
Корни
уравнения находим по формулам:
, 