21.Построение аксонометрической проекции: прямоугольной изометрии и косоугольной фронтальной диметрии.

Аксонометрическая проекция называется прямоугольной, если при параллельном проецировании проецирующие лучи перпендикулярны картинной плоскости (=90) и косоугольной, если лучи составляют с картинной плоскостью угол 0<<90

При этом используются приведенные коэффициенты искажения: для изометрических проекций Kx = Ky = Kz = 1, для диметрических проекций Kx = Kz = 1; Ky = 0,5.

Наряду с прямоугольными аксонометрическими системами на практике применяют некоторые косоугольные системы. Распространено применение аксонометрических проекций, когда аксонометрическая плоскость параллельна какой-либо ортогональной плоскости проекций. В машиностроительном черчении широкое применение получили косоугольные аксонометрии, полученные путём проецирования деталей на аксонометрическую плоскость, параллельную фронтальной плоскости проекций. Такая аксонометрическая система называется косоугольной фронтальной аксонометрией.

22.Преобразование проекций методом вращения вокруг проецирующих прямых и линий уровня.

Сущность способов вращения заключается в том, что заданную геометрическую фигуру путём вращения вокруг некоторой оси перемещают в пространстве до тех пор, пока она не займёт частное положение относительно плоскостей проекций.

Эффективным приёмом, упрощающим решение задач, связанных с определением метрических характеристик плоских фигур, является способ вращения этих фигур вокруг их линий уровня. Путём такого вращения можно плоскость, которой принадлежит рассматриваемая фигура, повернуть в положение, параллельное плоскости проекции.

(Сущность способа в том, что путём вращения вокруг линий уровня плоскость, в которой расположена фигура, переводится в положение, параллельное той плоскости проекций, которой параллельна прямая частного положения (линия уровня)).

При этом плоская фигура будет без искажения проецироваться на эту плоскость проекций.

При вращении вокруг горизонтали плоская фигура переводится в положение, параллельное плоскости H, при вращении вокруг фронтали в положение, параллельное плоскости V.

23.Преобразование проекций методом замены плоскостей проекций.

Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 8.4). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 8.5). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

24.Развёртки призматических и цилиндрических поверхностей. Развёртки пирамидальных и конических поверхностей.

Пирамидальных и конических

При развертывании поверхности на плоскости каждой точке поверхности соответствует единственная точка на развертке: линия поверхности переходит в линию развертки; длины линий, величины плоских углов и площадей, ограниченных замкнутыми линиями, остаются неизмеренными. Таким образом, процесс построения развертки сводится к отыскиванию натуральной (истинной) величины каждого элемента поверхности и изображению их на плоскости.

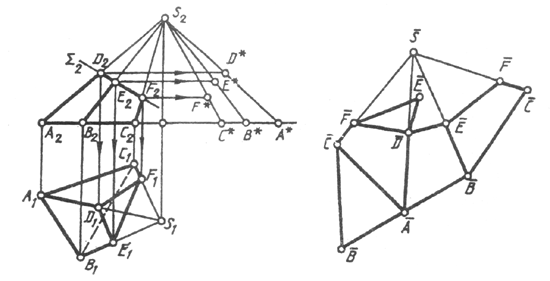Каждая боковая грань на развертке строится как треугольник по трем сторонам. CS — самое короткое боковое ребро, поэтому рациональнее мысленно разрезать пирамиду по этому ребру.

Для нанесения на развертку точек D, Е и F, соответствующих вершинам сечения пирамиды плоскостью Sum, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники АBС и DEF, дающие истинную величину основания и сечения пирамиды.

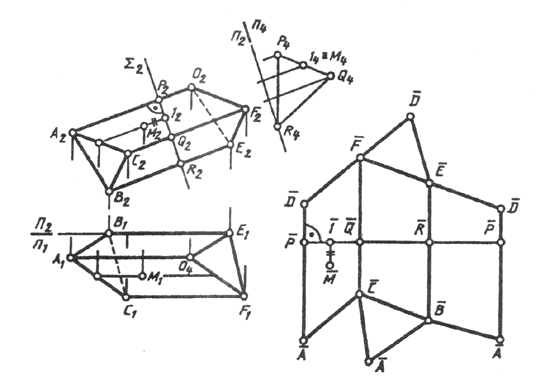
Развертки призматических и цилиндрических поверхностей

Развертки призматических и цилиндрических поверхностей строят способом нормального сечения. Поверхность рассекают плоскостью, перпендикулярной ее образующим (ребрам), и определяют истинную величину нормального сечения. Линию нормального сечения развертывают в прямую. Тогда образующие (ребра) поверхности при развертке ее на плоскость располагаются перпендикулярно развертке линии нормального сечения, которую принимают за базу отсчета размеров образующих (ребер).

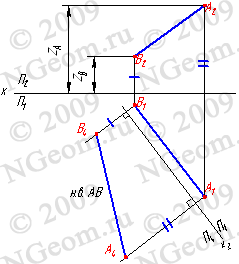
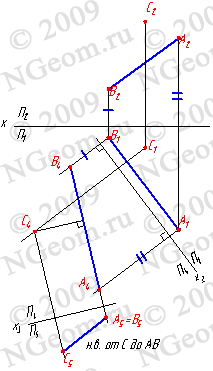
25.Определение натуральной величины отрезка. Определение расстояния от точки до прямой. Определение расстояния от точки до плоскости. Определение расстояния между паролельными и скрещивающимися прямыми ,между 2 плоскостями.

http://trivida.ru/chertezhi_view_post.php?id=19

Некоторые задачи на определение расстояний рассматривались в предыдущих разделах. Например, в § 42 определялась натуральная величина отрезка прямой линии методом треугольника, в § 57 определялась натуральная величина отрезка способом плоскопараллельного переноса. Эта задача может быть также решена способом замены плоскостей проекций (см. § 58) или способом вращения (см. § 59). Определение длины отрезка прямой позволяет решить задачу определения расстояния от точки до точки, так как это расстояние и определяется отрезком прямой. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать чертеж данной прямой, сделав ее в новой системе плоскостей проекций проецирующей (см. § 58, задача 2). На рис. 140 определено расстояние от точки М до прямой АВ:

При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.