15.Построение линии пересечения поверхностей на пкч, когда одна или две из них является проецирующими.

При построении линии пересечения двух поверхностей способом вспомогательных секущих плоскостей секущие плоскости, принятые в качестве посредников, могут быть и общего, и частного положения. Более широкое применение находят плоскости частного положения.

Плоскости общего положения применяются в ограниченных случаях. Например, их удобно использовать при построении линии пересечения конических и цилиндрических, а также пирамидальных и призматических поверхностей общего вида, когда основания этих поверхностей расположены в одной и той же плоскости.

Решение задачи построения линии пересечения двух поверхностей способом вспомогательных секущих плоскостей рассмотрим на примере пересечения конуса вращения со сферой. В качестве поверхностей-посредников примем плоскости частного положения— горизонтального уровня. На рис. 132 сначала отметим очевидные общие точки А и В поверхностей в пересечении их главных меридианов f и 1-S-2, так как поверхности имеют общую фронтальную плоскость симметрии Ф(Ф1); f2^S2—S2 = А2(В2); A2Al(B2Bl)|| S2S1, A2Al(B2Bl) ^f1 =A1(B1)

Эти опорные точки являются наивысшей А и наинизшей В точками линии пересечения, а также точками видимости линии на плоскости П2.

Брать вспомогательные фронтальные плоскости, параллельные П2, для построения следующих точек неудобно, так как они будут пересекать конус по гиперболам. Графические простые линии (окружности параллелей) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г.

Первую такую вспомогательную плоскость Г1 берем на уровне экватора сферы И. Эта плоскость пересекает конус по параллели h1.В пересечении этих параллелей находятся точки видимости линии пересечения относительно плоскости П1:

h1^h11 = С1(D1); С1С2|| S1S2; С1С2 ^ h2(hl2) = C2(D2).

Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии (рис. 133), то самую высокую А и низкую В точки линии пересечения поверхности легко определить, построив изображения этих поверхностей на плоскости П4, параллельной осевой плоскости Sum (Sum1) данных поверхностей. Можно построить проекции всей линии пересечения в системе плоскостей П1_|_П4, а затем построить ее фронтальную проекцию в проекционной связи с горизонтальной проекцией, замеряя высоты точек на плоскости П4,так, как это показано на рис. 132 для точек А и В.

16.Построение линии пересечения поверхностей способом вспомогательных секущих плоскостей.

Вспомогательные секущие плоскости чаще всего выбирают проецирующими и параллельными одной из плоскостей проекций - плоскостями уровня.

Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

1. Если образующие (окружности) расположены в общих плоскостях уровня;

2. Если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;

3. Линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.

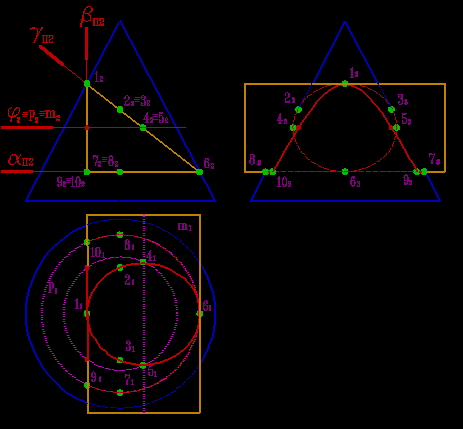
Пример 1: Рассмотрим построение линии пересечения треугольной призмы с конусом (рис.8.31) . Пусть ось вращения конуса перпендикулярна плоскости П1, а грани призмы перпендикулярны плоскости П2.

В этом случае призму можно рассматривать, как три плоскости α, β, γ, проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом. При этом в соответствии с характерными сечениями конуса известно, что плоскость α пересекает конус по окружности параллельной П1, β- по гиперболе параллельной П3, а γ- по эллипсу.

На плоскость П2 линии пересечения от всех плоскостей проецируются в прямые, совпадающие со следами плоскостей α, β, и γ.

Для построения проекций этих линий на плоскости П1 и П3 отметим характерные точки на уже имеющейся фронтальной проекции линий пересечения:

Точки 12 и 62 – пересечения плоскости γ с очерком проекции конуса на плоскость П2 (главным меридианом), эти точки определяют положение большой оси эллипса, кроме того точка 12 –проекция точки вершины гиперболы и одновременно принадлежит конусу (лежит на очерке фронтальной проекции конуса) и ребру призмы (линии пересечения плоскостей α и β), а точка 62- проекция точки, одновременно принадлежащей конусу и ребру призмы (линии пересечения плоскостей α и γ); точки 2, 3, 7 и 8 – характерны тем, что их профильные проекции лежат на очерке проекции конуса; 42, 52- точки, лежащие на середине отрезка 1262 (большой оси эллипса) и определяют положение малой оси эллипса; 9,10 – точки одновременно принадлежащие конусу и ребру призмы (образованному пересечением плоскостей α и β).

Рассмотрим последовательность нахождения проекций точек 4 и 5. Через фронтальные проекции этих точек проведем вспомогательную секущую плоскость φ. Эта плоскость пересекает конус по параллели p, а грань призмы по прямой линии m, параллельной ребру. На горизонтальной плоскости проекций пересечение p 1 и m 1 определяют положение точек 41 и 51. Для точного построения кривых линий пересечения поверхностей обозначенных точек не достаточно. После нахождения проекций всех точек их необходимо соединить с учетом видимости.