11.Многограники(призма и пирамида) на пкч(точка и линия на поверхности) и их сечения проецирующими плоскостями.

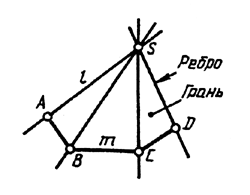
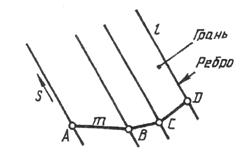
Грани призм и пирамид ограничиваются ребрами, являющимися прямолинейными отрезками, пересекающимися между собой. Поэтому построение чертежей призм и пирамид сводится по существу к построению проекций точек (вершин) и отрезков прямых - ребер.

Призматическая поверхность на чертеже может быть, изображена проекциями фигуры, полученной при пересечении боковых граней призмы плоскостью, и проекциями ребер призмы. Пересекая призматическую поверхность двумя параллельными между собой плоскостями, получают основание призмы. На чертеже основания призмы удобно располагать параллельно плоскости проекций.

Плоскость пересекает пирамиду по многоугольнику. Если плоскость параллельна основанию пирамиды, в сечении получается фигура, подобная основанию. При построении линии пересечения

пирамиды с плоскостью определяют точки пересечения ее ребер с данной плоскостью или строят линии пересечения граней пирамиды с этой плоскостью. Натуральная величина сечения определена способом замены плоскостей проекции.

При построении линии пересечения призмы с плоскостью определяют точки пересечения ее ребер с данной плоскостью. Эту линию можно также построить, определяя линии пересечения отдельных граней призмы с плоскостью. В результате пересечения поверхности призмы плоскостью может быть получен прямоугольник если эта плоскость параллельна боковым рёбрам призмы, или различного вида многоугольники если плоскость не па параллельна им треугольной призмы фронтально-проецирующей плоскостью .

12.Представление цилиндра и конуса на пкч. Конические сечения.

В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые вершину конуса, в его сечении получается пара прямых - образующие конуса . В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность .

13.Представление шара и тора в пкч. Точка и линия на поверхности. Сечение шара и тора проецирующими плоскостями.

Когда некоторая ось вращения I является диаметром окружности, то получается шаровая поверхность).

Если положение оси другое, в плоскости окружности получается поверхность, называемая тором .

Тор – это поверхность, получаемая в результате вращения окружности около оси, которая лежит в ее плоскости, не проходящей через ее центр.

В пересечении тора с плоскостью могут быть получены различного рода кривые линии. Если плоскость проходит через ось вращения тора, в сечении получаются две окружности - образующие, если плоскость перпендикулярна к оси вращения, в сечении получаются две окружности - параллели.

Любая плоскость пересекает сферу по окружности. Если секущая плоскость параллельна плоскости проекций, окружность сечения проецируется на эту плоскость проекций без искажения. Если секущая плоскость не параллельна ни одной из плоскостей проекций, проекциями окружности являются эллипсы.

14.Сущность метода посредников- общего метода построения линии пересечения поверхностей.

При разработке конструкторской и технологической документации различных изделий (например, сложных составных воздуховодов) часто возникает необходимость построения линий пересечения поверхностей. Линии взаимного пересечения поверхностей проще всего построить графически по точкам с помощью поверхностей-посредников. Рассмотрим сущность этого метода.

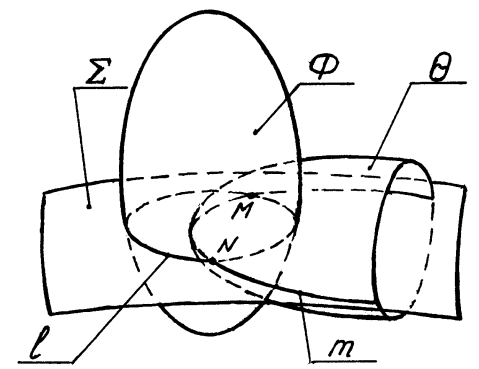
Пусть заданы две пересекающиеся поверхности  и Θ (рис. 16).

Для построения точек линии пересечения этих поверхностей введем вспомогательную секущую поверхность , которая пересечет поверхности  и Θ по линиям l и m соответственно. Линии l и m пересекутся между собой в точках М и N, поскольку они принадлежат одной поверхности . Точки M и N будут лежать на линии пересечения поверхностей  и Θ, так как эти точки лежат одновременно на обеих пересекающихся поверхностях.

В качестве вспомогательных секущих поверхностей-посредников обычно применяют плоскости и сферы. Поэтому способы реализации метода посредников называют способами секущих плоскостей и секущих сфер.

Вспомогательные секущие плоскости в большинстве случаев параллельны плоскостям проекций. Однако в отдельных случаях для определения точек линии пересечения поверхностей рациональнее воспользоваться наклонными плоскостями (способ вращающейся или качающейся плоскости).

Способ сфер имеет две разновидности – способ эксцентрических сфер (центры секущих сфер не совпадают) и способ концентрических сфер (сферы имеют один общий центр). Большинство задач на взаимопересечение поверхностей решают рассматриваемым здесь способом концентрических сфер. Способ эксцентрических сфер используют только в том случае, когда одна из пересекающихся поверхностей имеет криволинейную ось и круговые сечения.

Рис 98

В каждом конкретном случае выбирают тот способ построения точек линии пересечения поверхностей, который позволяет выполнить наиболее простые графические построения.