8.Пересечение прямой и плоскости, когда прямая или плоскость занимают частное положение; прямая и плоскость занимают общее положение.

9.Построение линии пересечения двух плоскостей в частном и общем положении.

Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей. На рис. 122 приведен комплексный чертеж двух пересекающихся плоскостей £ и 0, причем плоскость Sum частного положения — фронтально проецирующая. Она пересекает линии АВ и АС плоскости 0, данной треугольниками ABC — плоскости общего положения. Точки пересечения 1 и 2 и определяют линию пересечения плоскостей. Соединив их, получаем искомую линию: a(1, 2) = Sum^Q.

Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекции. Для этого дважды решают задачу на построение прямой одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекции, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей.

На рис. 123, а построена линия пересечения двух треугольников ABC и DEF путем построения точки М пересечения линии АВ с плоскостью DEF и точки N пересечения линии EF с плоскостью АВС:

Рис 123

Рис .122

10.Поверхность. Образование поверхности. Виды поверхности. Задания поверхности на чертеже. Гранные, цилиндрические и конические поверхности. Поверхности вращения. Характерные линии на поверхности вращения. Линейчатые поверхности. Приближенная классификация поверхностей.

Поверхность- в инженерной графике поверхность рассматривают как множество последовательных положений линии, перемещающейся в пространстве по определенному закону. В процессе образования поверхности линия может оставаться неизменной или менять свою форму.

Любую поверхность можно получить различными способами

Подвижную линию принято называть образующей, неподвижные - направляющими. Такой способ образования поверхности принято называть кинематическим.

Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.

По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.

Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.

Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Это так называемые циклические поверхности.

Виды поверхности:

Цилиндрические поверхности.

Сферическая поверхность.

Поверхность вращения

Винтовая поверхность

Коническая поверхность

Циклическая поверхность

Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать внутренние свойства поверхности. При проектировании поверхностей технических форм и их воспроизведении на станках с программным управлением используются совместно графические и аналитические способы задания поверхностей.

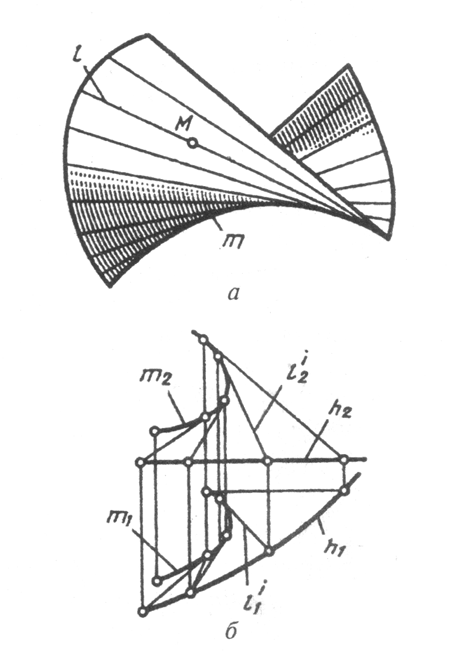
К коническим относятся поверхности, образованные перемещением прямолинейной образующей l по криволинейной направляющей т. Особенностью образования конической поверхности является то, что при этом одна точка образующей всегда неподвижна. Эта точка является вершиной конической поверхности (рис. 95, а). Определитель конической поверхности включает вершину S и направляющую т, при этом l'~S; l'^ т.

К цилиндрическим относятся поверхности, образованные прямой образующей /, перемещающейся по криволинейной направляющей т параллельно заданному направлению S (рис. 95, б). Цилиндрическую поверхность можно рассматривать как частный случай конической поверхности с бесконечно удаленной вершиной S.

Рис 96

Рис 95

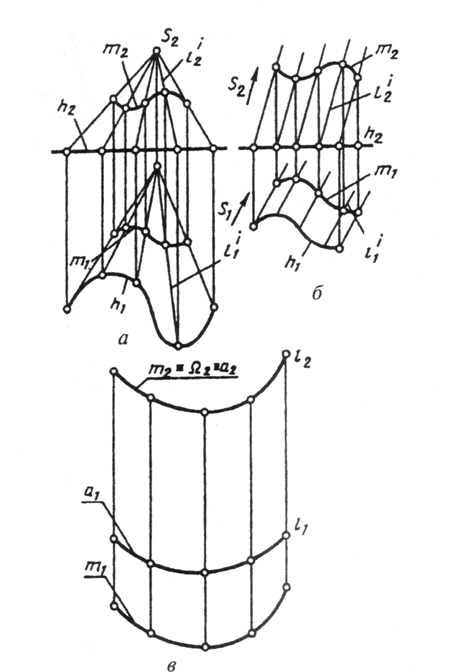
К гранным относятся поверхности, образованные перемещением прямолинейной образующей l по ломаной направляющей т. При этом если одна точка S образующей неподвижна, создается пирамидальная поверхность (рис. 97), если образующая при перемещении параллельна заданному направлению S, то создается призматическая поверхность (рис. 98).