2.4. Вычисление значений арифметических выражений в экономических задачах
В качестве примеров экономических задач рассмотрим несколько условных задач, в том числе и задач из нашего исторического прошлого. Как говорил Конфуций: "Без прошлого нет будущего".
Пример 3. Предприятие отчислило в фонд социального страхования в 1-ом квартале текущего года – С1, а во втором – С2 тыс. руб. Определить общую сумму отчисления в фонд социального страхования предприятием.
Очевидно, что общая сумма отчислений равна С1+С2. Выполним вычисления средствами MathCAD.
1. Выведите на экран панель Калькулятор (рис. 3).
2. Установите курсор в нужное место экрана.
3. Для получения общей суммы присвойте вначале переменным: С1 и С2, – некоторые произвольные значения, используя оператор присваивания на панели Калькулятор, а затем запишите выражение, вычисляющее общую сумму. Алгоритм и результат появятся на экране (рис. 9).
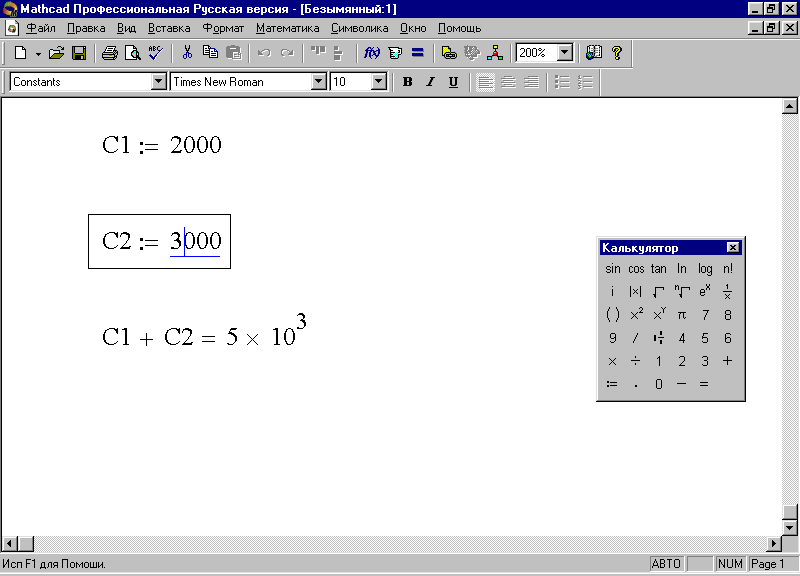
Рис. 9. Вычисление отчислений в фонд социального страхования
Пример 4. В конце 20-х годов XIX века в нашей республике начали возникать районы сплошной коллективизации, т.е. районы, в которых процент коллективизации превышал 80%. Имеются данные тех лет по хозяйствам Минского округа.
Определить общее количество хозяйств, которые были коллективизированы на начало 1935 года по Минскому округу.
Присвоим исходным данным условные обозначения и сведем их в таблицу 2 следующей формы:
Коллективизация
Таблица 2
-
Год
1929
1930
1931
1932
1933
1934
Количество коллективизированных хозяйств
К1
К2
К3
К4
К5
К6
Очевидно, что в задаче требуется найти К=К1+К2+К3+К4+К5+К6. Алгоритм и результат вычисления представлены на рис. 10.
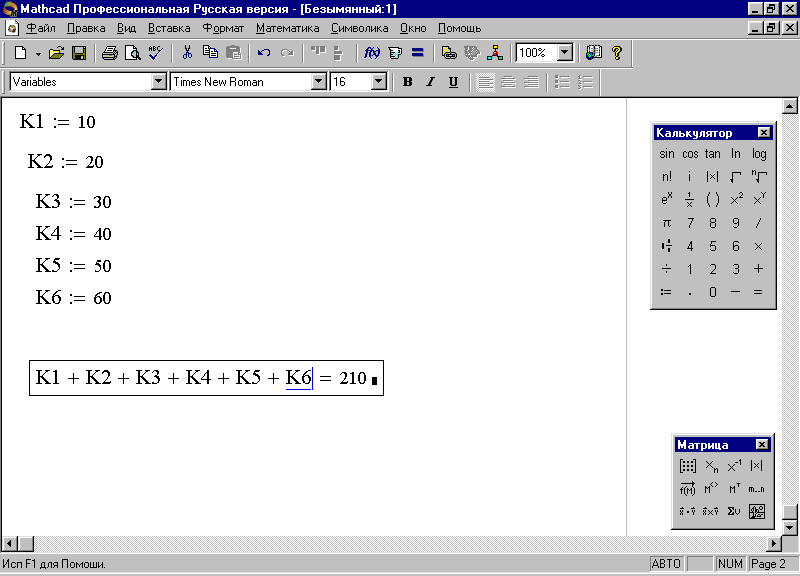
Рис. 10. Определение общего количества коллективизированных хозяйств
Пример 5. Предприятие ежемесячно К-ую часть своего дохода отчисляет на оказание шефской помощи школе. Определить, какую сумму предприятие отчислило за квартал, если доход по месяцам квартала соответственно составил: Х1, Х2, Х, млн. руб.
Требуется сложить компоненты: Х1, Х2 и Х3, а затем полученную сумму умножить на 1/К, или разделить на К:
С=
Х1+Х2+Х3
К
Алгоритм и результат решения при К=10 представлены на рис. 11.
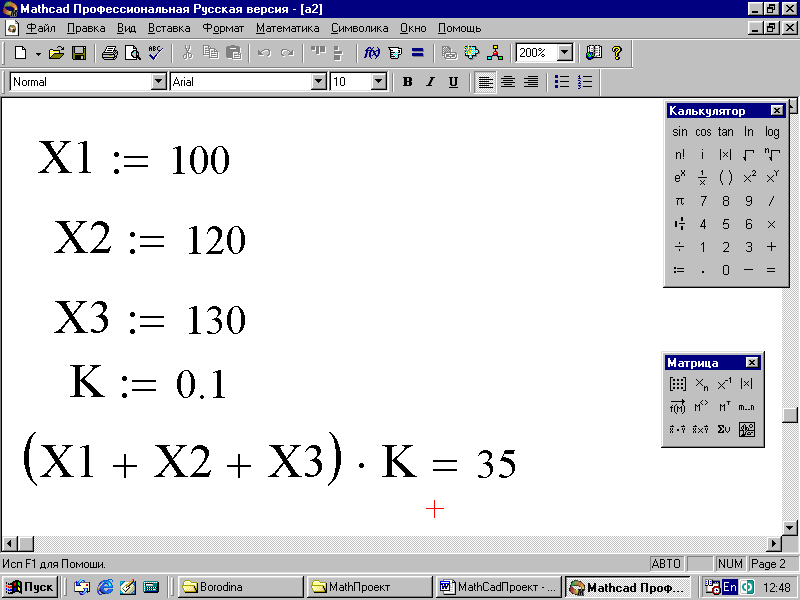
Рис. 11. Определение отчислений предприятием за квартал
Пример 6. Рента, которая накладывалась на крестьянское хозяйство Белоруссии, могла быть трех видов: отработочная, продуктовая, денежная. В год крестьянское хозяйство должно было:
сдать 360 грошей деньгами;
отработать 2 дня в неделю из расчета 49 рабочих недель в году;
сдать одну бочку ржи, одну курицу, 20 яиц.
Определить сумму ренты в грошах на одно крестьянское хозяйство, а также процентное соотношение всех видов ренты, если известно, что:
один день барщины равен одному грошу,
одна бочка ржи – 360 грошей,
одна курица – 10 грошей,
1 яйцо –1 грош.
Очевидно, что алгоритм расчета сведется, прежде всего, к вычислению общей суммы ренты в грошах по следующей формуле: 360+2*49+360+10+20. А затем надо найти процентное отношение суммы каждого вида ренты к вычисленной общей сумме в грошах (рис. 12).
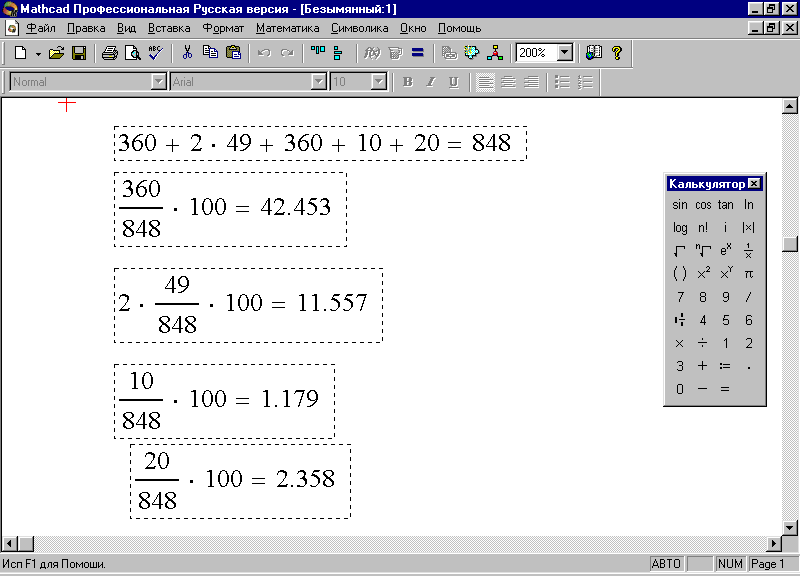
Рис. 12. Вычисление ренты