2.3. Встроенные функции

Система MathCAD содержит библиотеку готовых встроенных функций, которые делятся на категории: тригонометрические, например: sin, cos, tan; финансовые, например: nom, pmt; статистические, например: corr, hist и др.

Пример 2. Определить значение арктангенса следующего выражения:

; если X=5, Y=6.

1. Выведите панель Калькулятор и наберите x:=5 y:=6.

2. Начните вводить выражение, для чего поместите курсор в нужную точку рабочей области и наберите Х (рис.5).

3. Для того чтобы Х возвести в степень, нажмите сочетание клавиш [Shift+6]. При этом курсор переместится на место будущего показателя степени, и появится черный маркер-шаблон, предназначенный для ввода. В него следует ввести требуемый показатель. Показатель возведения в степень можно задать также с панели Калькулятор кнопкой [x^y].

Рис. 5. Вычисление факториала и арктангенса

4. Косинус можно ввести как с панели Калькулятор, так и набрать на клавиатуре. Во втором случае нужно помнить, что в MathCAD аргумент функции необходимо заключать в скобки.

5. Наберите Х, затем введите с клавиатуры знак деления [/] и наберите Y. После того, как вы набрали X/Y, в нашей формуле нужно поставить закрывающую круглую скобку, если вы набирали функцию на клавиатуре. Для этого выделите все отношение, охватив его линиями ввода. Это можно сделать, нажимая последовательно необходимое количество пробелов (таким способом можно выделить любую часть формулы). После чего введите круглую скобку.

6. Чтобы умножить весь набранный фрагмент на натуральный логарифм, выделите этот фрагмент последовательным нажатием пробела, нажмите знак умножения [х], выбрав его на панели Калькулятор, и введите натуральный логарифм либо с клавиатуры, либо с панели Калькулятор.

Запомните! При введении произведения х и у нельзя просто написать ху, так как такое произведение будет воспринято как новая, не определенная функция. Нужно обязательно поставить знак умножения.

7. Корень произвольной степени введите сочетанием клавиш [Ctrl+\], или с панели Калькулятор (обычный квадратный корень можно ввести клавишей [\]).

8. Чтобы перейти к набору знаменателя, выделите, то есть охватите выделяющей линией, набранную часть функции в числителе, нажимая знак пробела, после чего введите знак деления.

9. Нажмите на знак модуля на панели Калькулятор – это кнопка [Абсолютное значение] и завершите ввод выражения в знаменателе.

10. Чтобы взять все выражение под знак функции арктангенса, выделите его и разверните вертикальную линию ввода влево клавишей [Insert]. Кроме того, для редакции любого фрагмента можно перемещать курсор при помощи клавиш управления движением курсора, либо мышью.

11. Функции арктангенса нет на панелях инструментов, поэтому ее нужно взять из библиотеки (списка) встроенных функций. Вызвать этот список можно либо сочетанием клавиш [Ctrl+E], либо, выполнив команду Вставка>Функция, либо при помощи кнопки [f(x)] – Вставить функцию на панели инструментов. В открывшемся окне Вставить Функцию (рис. 6) имеется: список категорий функций, список функций выбранной категории, а также окно информации о выбранной функции. По умолчанию определена категория АLL (Все), и в окне находится полный список всех встроенных функций MathCAD.

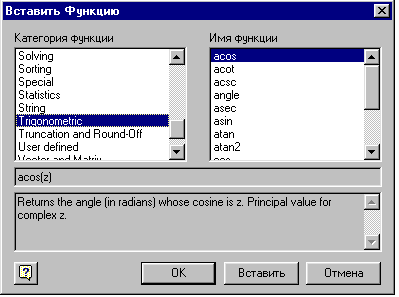
Рис. 6. Окно для выбора встроенной функции

Очевидно, что арктангенс нужно искать в категории Тригонометрических функций (Trigonometric). Среди тригонометрических функций находится два вида арктангенса: Atan и Atan2. Atan(Z) – возвращает угол (в радианах), для которого тангенс – это Z. Здесь Z может быть комплексным числом. Atan2(X,Y) – возвращает угол (в радианах) между осью X и линией, содержащей точку начала координат и точку (X,Y). Здесь X и Y должны быть действительными. Нам нужно использовать функцию Atan(Z). Выберите ее и нажмите [OK] – выражение с арктангенсом будет. Для вычисления значения введенного выражения следует нажать знак равенства.

Параметры введенного выражения, установленные по умолчанию, не всегда удовлетворяют пользователя. Для того чтобы отредактировать вид выражения, нужно при помощи команды Формат>Вычисление вызвать окно Формат Уравнения (рис. 7), позволяющее определить цвет шрифта формул, выбрать стиль. При помощи кнопки [Изменить] можно изменить стиль текста формул: выбрать тип, размер, начертание шрифта.

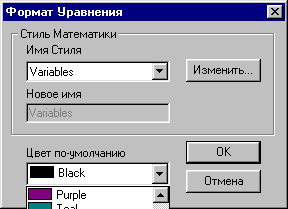
Рис. 7. Формат уравнения

Чтобы поменять параметры самой математической области, следует выполнить щелчок мышью по любой точке редактируемой формулы и в контекстном меню выбрать команду Свойства (Properties). Откроется окно свойств Properties (рис. 8), где указаны средства, позволяющие взять формулу в рамку (установить флажок Вкл Границу), сделать область цветной при помощи команды Фон>Подсветка Региона>[Выбор цвета].

Области формул можно перемещать по экрану с помощью мыши, аналогично любым окнам Microsoft Windows. Редактируя формулы, можно вырезать и копировать их фрагменты так же, как в других приложениях Windows.

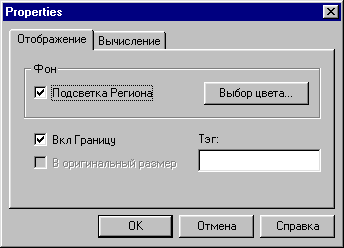
Рис.8. Окно Свойства