2.19.2. Решение с помощью параболического сплайна
Сплайн – это математическая модель гибкого, тонкого стержня из упругого материала. Стержень закрепляется в двух соседних узлах с заданными углами наклона. Стержень длиннее, чем расстояние между двумя точками. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закреплённую в узловых точках (откуда и название: spline – гибкая линейка).
Функция pspline(vx,vy) – возвращает вектор коэффициентов кубического сплайна vs, который используется функцией interp для построения кубического сплайна, интерполирующего данные, представленные в векторах vx и vy. На поведение сплайна на концах условий не налагается. Вектор vs становится первым параметром функции interp.
Функция interp(vs,vx,vy,x) – возвращает интерполированное значение в точке х, полученное с помощью кубических сплайнов на основе данных, представленных в векторах vx и vy:
Найдите вектор кубического сплайна:
kp:=pspline(X,Y)
Определите значение функции при заданном значении аргумента:
YD := interp(kp,X,Y,XD)
YD = 5.815
Найдите функцию, заданную таблицей, с помощью параболического сплайна:
fp(x) := interp(kp,X,Y,X)
6.616
7.399
6.196
fp= 6.005
7.825
5.655
4. Постройте график найденной функции (рис. 88).
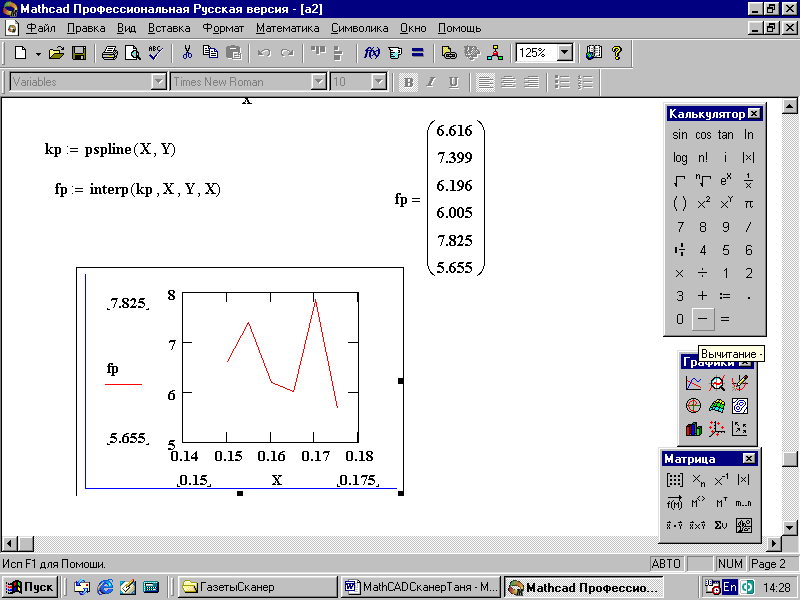
Рис. 88. Решение с помощью параболического сплайна
Решение с помощью линейной аппроксимации
Линейная аппроксимация выполняется с помощью функций: intercept и slope, которые позволяют найти коэффициенты аппроксимирующего полинома.
Функция intercept(vx,vy) – это свободный член уравнения регрессии, который равен отрезку, отсекаемому линией регрессии на оси ординат.
Функция slope(vx, vy) – коэффициент линейного уравнения регрессии, которая определяет тангенс угла наклона линии регрессии к оси.
1. Примените эти функции для получения свободного члена и коэффициента регрессии:
a0 := intercept(X,Y), a1 :=slope(X,Y).
2
.
Запишите аппроксимирующий полином и
получите приближенное значение функции
в заданной точке:
6.882
6.775
r(X)= 6.669
r(X):=a0 + a1 • X 6.563
6.457
r(XD) = 6.627 6.35
3. Постройте график аппроксимирующего полинома и таблично заданной функции (рис. 89).
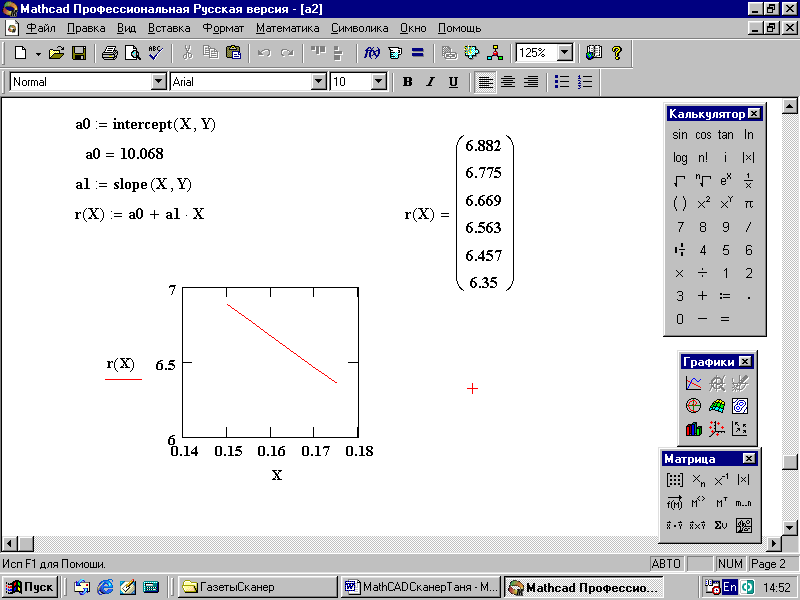
Рис. 89. Решение с помощью линейной аппроксимации
2.19.4. Графики таблично заданной функции в одних осях координат
Для сравнения всех функций и полученных вычислений построим общий график в одних осях координат (рис. 90):
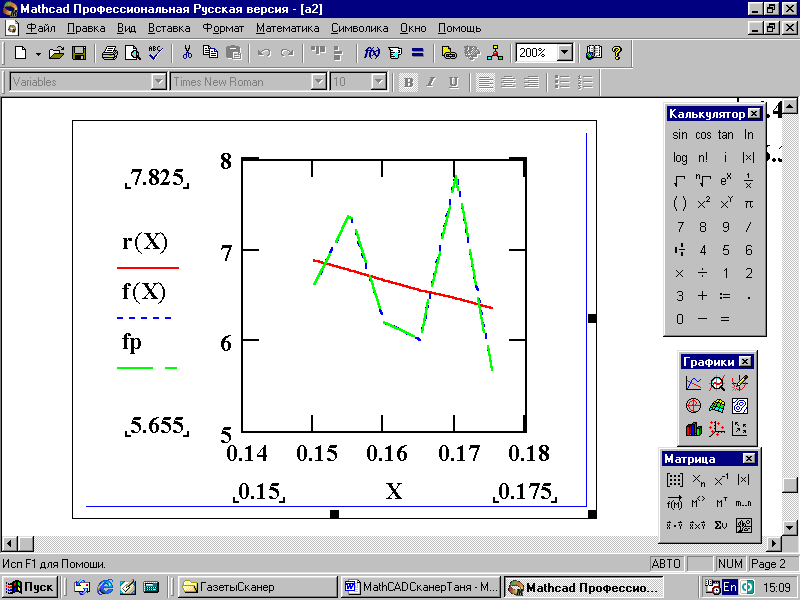
Рис. 90. Графики таблично заданной функции в одних осях координат
Проведя исследование функции различными методами, мы получили лишь примерно одинаковые результаты. Это вызвано тем, что при исследовании разными методами таблично заданная функция ведет себе по-разному. Но при исследовании функции с помощью метода наименьших квадратов и полиномиальной регрессии при одинаковых значениях порядка полинома графики функций совпадают, что говорит о правильности всех вычислений. На это также указывает и тот факт, что, если посчитать среднеквадратичное отклонение, то оно получится меньше единицы: Е=0.759.