2.19. Интерполяция и аппроксимация
В MathCAD имеется несколько способов интерполяции и экстраполяции (предсказания):
Линейная интерполяция – соединение точек прямой линией;
Кубическая сплайновая интерполяция – соединение точек с использованием кубических линий;
Интерполяция В-сплайн – соединение точек с использованием многочленов определенной степени в данных узлах;
Многомерная кубическая сплайновая интерполяция – создание поверхности, проходящей через сетку точек;
Линейное предсказание (экстраполяция) – определение значений вне набора данных.
В MathCAD функции интерполяции определяют кривую, точно проходящую через заданные точки. При этом точки могут соединяться отрезками прямых или отрезками кубического полинома. Функции регрессии создают кривую или поверхность, которые наилучшим образом аппроксимируют исходные данные. В отличие от функций интерполяции, функции регрессии не требуют, чтобы аппроксимирующая кривая или поверхность проходили через точки исходных данных.
Пример 58. Для таблично заданной функции Y найти приближенное значение функции Y при конкретном значении аргумента X=0.162:
X Y Заданное значение аргумента
0.150 6.616 0.162
0.155 7.399
0.160 6.196
0.165 6.005
0.170 7.825
0.175 5.655
Решение выполнить следующими способами:
с помощью линейной интерполяции;
с помощью кубического сплайна;
с помощью линейной аппроксимации;
методом наименьших квадратов при m=2 и при m=3, где m – порядок полинома. Вычислить среднеквадратичное отклонение;
с помощью полиномиальной регрессии.
Построить графики: таблично заданной функции, интерполяционного полинома и аппроксимирующей функции, – в одних осях координат.
Решение различными способами рассмотрено далее.
2.19.1. Решение с помощью линейной интерполяции
При линейной интерполяции используется функция линейного интерполирования linterp(vx,vy,xd), которая возвращает оценку значения в точке x, вычисленную методом линейной интерполяции на основе значений векторов X и Y;
• vx – вещественный вектор, элементы которого должны идти в порядке возрастания и соответствовать значениям X;
• vy – вещественный вектор одного размера с vx. Его элементы соответствуют значениям Y;
• xd – значение переменной х, в которой нужно проинтерполировать величину y. Предполагается, что х лежит в интервале изменения элементов vx.
1. Задайте значения аргумента X и функции Y в виде матриц, а также задайте значение точки XD, в которой надо найти значение функции (рис.86):
0.150 6.616
0.155 7.399
X:= 0.160 Y:= 6.196 XD:= 0.162
0.165 6.005
0.170 7.825
0.175 5.655
2. Определите значение функции YD при заданном значении аргумента XD с помощью линейной интерполяции, воспользовавшись функцией linterp (рис. 86):
YD:= linterp(X,Y,XD); YD = 6.12.
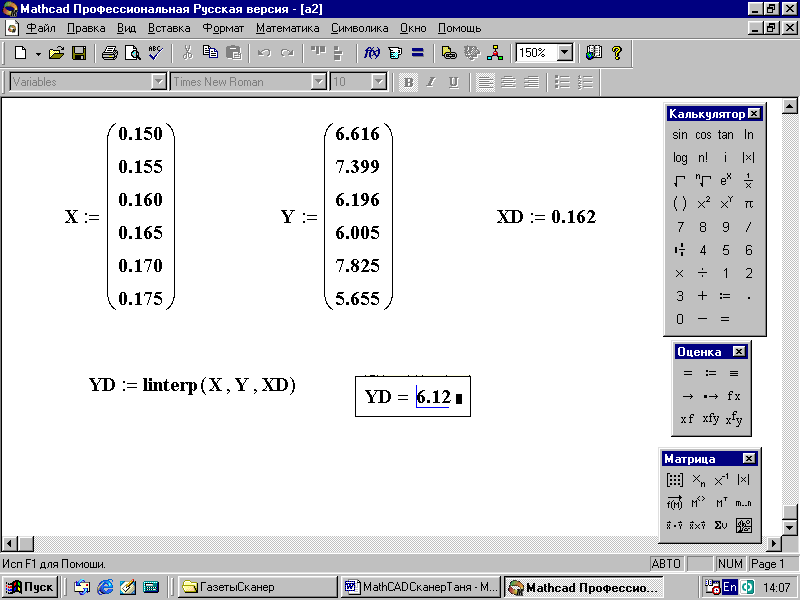
Рис.86. Решение с помощью линейной интерполяции
3. Для таблично заданного аргумента X и значения функции YD=6.12 в некоторой точке XD=0.162 найдите функцию f(X) в виде таблицы с помощью линейной интерполяции f(X):=linterp(X,Y,XD).
6.616
7.399
f(X) = 6.196
6.005
7.825
5.655
4. Постройте график функции f(X), – он проходит через заданные узлы интерполяции, значит, функция определена верно (рис. 87).
Рис. 87. График функции, полученный методом линейной интерполяции