2.17. Решение дифференциальных уравнений

При решении дифференциального уравнения искомой величиной является функция. Для обыкновенных дифференциальных уравнений неизвестная функция – это функция одной переменной. Для дифференциальных уравнений в частных производных – это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Пакет MathCAD имеет ряд встроенных функций, предназначенных для решения дифференциальных уравнений. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (некоторой сетке значений).

При использовании метода Рунге-Кутта, применяется функция rkfixed(y, x1, x2, n, f), которая выдает результат решения системы обыкновенных дифференциальных уравнений методом Рунге-Кутта четвертого порядка с фиксированным шагом интегрирования в виде таблицы. Ее можно использовать для решения как одного дифференциального уравнения, так и системы дифференциальных уравнений. Эта функция имеет пять аргументов:

• y – вектор начальных значений искомых функций;

• x1 – начальное значение независимой переменной;

• х2 – конечное значение независимой переменной;

• n – фиксированное число шагов интегрирования;

• F – правые части системы уравнений, записанные в виде вектора в символьном виде.

Пример 53. Решить методом Рунге-Кутта дифференциальное уравнение первого порядка y' = х + cos( y/1.25) при заданных начальных значениях: y₀(0.4)=0.8 и х [0.4, 1.4].

1. Запишите начальное значение Y₀ := 0.8 (рис. 79).

2. Запишите заданную функцию F(X,Y) :=X+ cos(Y/1.25).

3. Запишите встроенную функцию, выполняющую дифференцирование У:=rkfixed(Y₀,0.4,1.4,20,F),

где y₀ – вектор начальных значений искомой функции;

0.4 – начальное значение независимой переменной;

1.4 – конечное значение независимой переменной;

20 – количество шагов интегрирования;

F – правые части системы уравнений, записанные в виде вектора в символьном виде.

Функция rkfixed(y,x1,x2,n,F) выдает таблицу результатов решений с (m+1) столбцами и n строками, где m – число уравнений в системе. Нулевой столбец таблицы – это текущее значение независимой переменной (аргумента) х. Переменные определяются через x1, x2,… ,xn. Последующие столбцы решения определяют значения искомых функций y₁(x), y₂(x),… для соответствующих значений аргумента х (рис. 80-81).

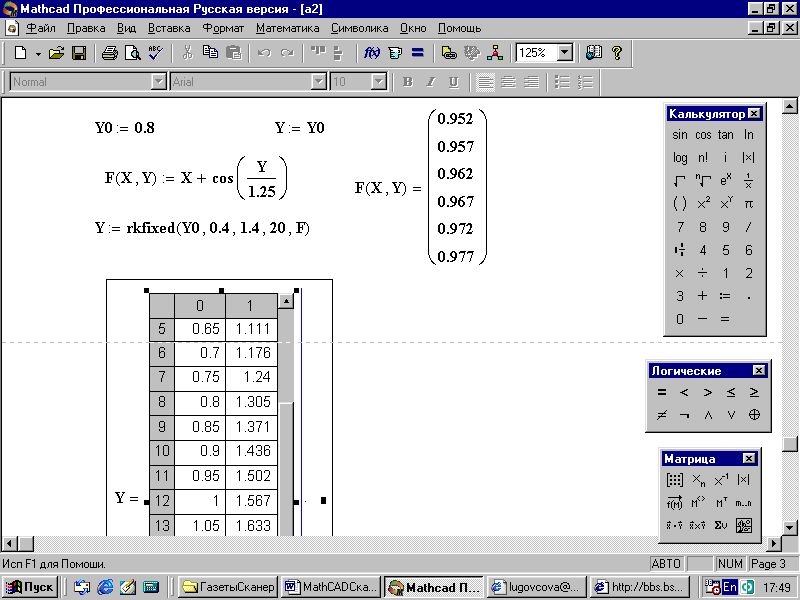
Рис. 80. Решение дифференциального уравнения методом Рунге-Кутта (начало)

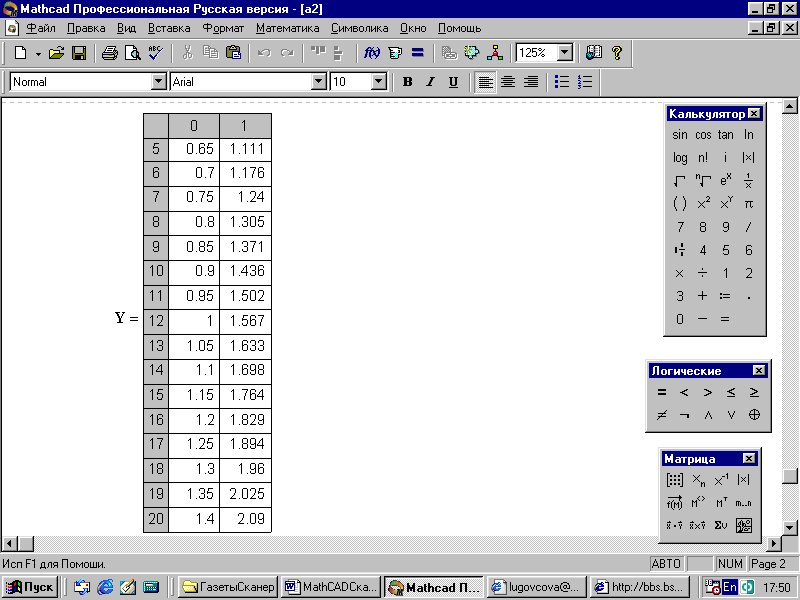
Рис. 81. Решение дифференциального уравнения методом Рунге-Кутта (конец)

Пример 54. Решить дифференциальное уравнение f''(x)-f(x)=х при заданных начальных значениях: f(0)=3, f(6)=140, используя функцию odesolve.

Алгоритм и результат решения представлен на рис. 82.

Рис. 82. Решение дифференциального уравнения

18. Символьные преобразования

MathCAD позволяет выполнять символьное преобразование выражений. Для этих целей используется кнопка [Символьное преобразование] на панели Оценка.

Пример 55. Выполнить символьные преобразования следующих формул: (x²+2*x*y+y²)*2; (x+y)*x+5*(x²-x); x*(x+y).

1. Установите курсор и, активизировав панель Калькулятор, наберите заданную формулу:

2. Окружите полностью выражение выделяющей рамкой.

3. Выполните символьные преобразования, воспользовавшись командой Символика>Упрощение, или кнопкой [Символическое Вычисление] на панели Оценка, – на экране появится результат (рис. 83).

4. Аналогичные действия выполните для символьного преобразования двух других формул (рис. 83).

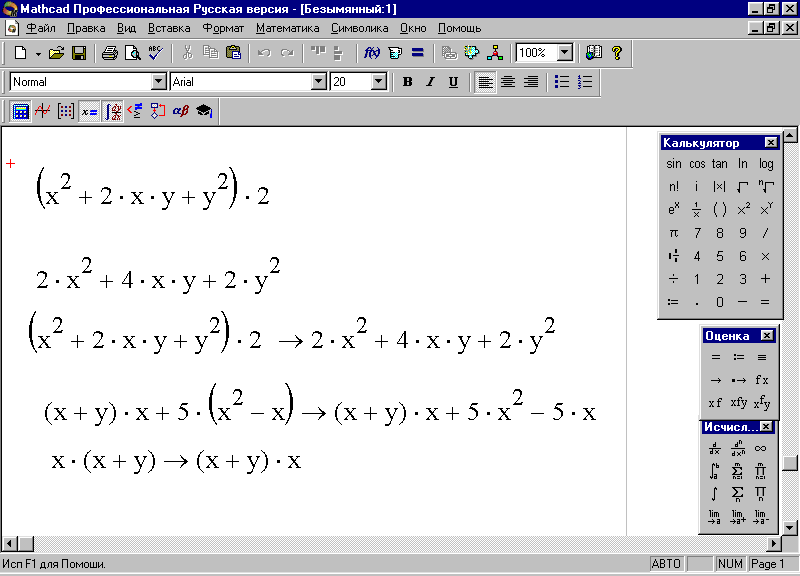
Рис. 83. Символьные преобразования формул

Пример 56. Выполнить символьное решение следующей системы линейных уравнений:

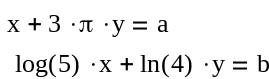
1. Для решения заданной системы уравнений установите панели: Калькулятор, Оценка и Логические.

2. Наберите на клавиатуре служебное слово given.

3. Под словом given наберите заданные уравнения, используя знак [Равно], расположенный на панели Логические.

4. Наберите на клавиатуре встроенную функцию find (x,y).

5. Нажмите кнопку [Символическое Вычисление] на панели Оценка, – алгоритм и результат решения представлены на рис. 84.

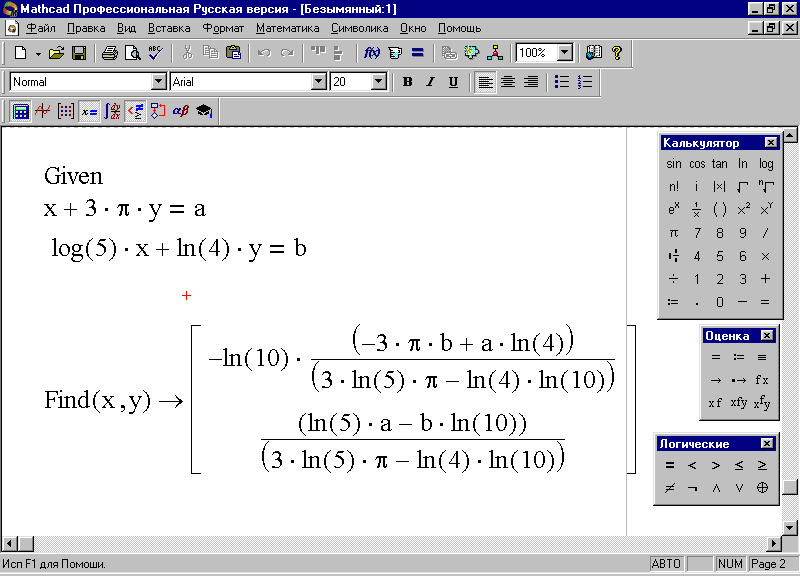
Рис. 84. Символьное решение системы линейных уравнений

Пример 57. Выполнить символьное решение следующей системы нелинейных уравнений:

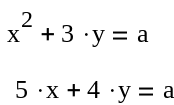
Алгоритм решения аналогичен предыдущему примеру. Алгоритм и результат решения представлены на рис. 85.

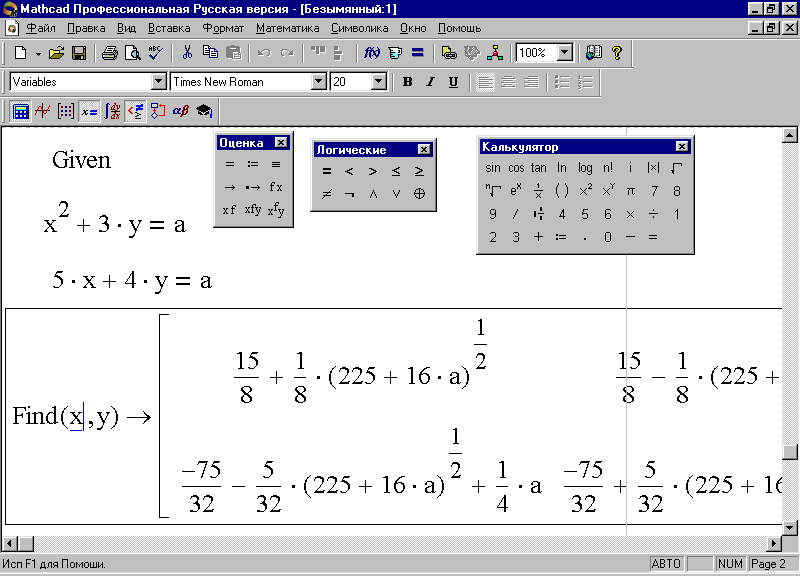
Рис. 85. Символьное решение системы нелинейных уравнения