15. Нахождение экстремума

В системе MathCAD имеется ряд средств, а именно встроенных функций, для нахождения экстремума как последовательностей, так и функций: Max, Min, Maximize, Minimize (рис. 75).

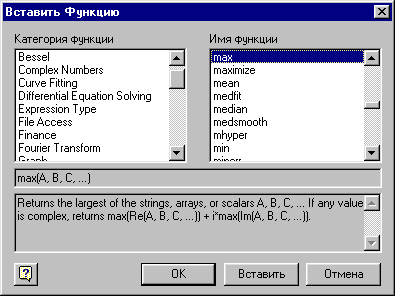
Рис. 75 Окно Вставить Функцию

Пример 46. Найти максимум и минимум заданной последовательности чисел: 25, 38, 10, 70.

1. Установите курсор и активизируйте панель Калькулятор.

2. Вызовите встроенную функцию, определяющую максимум, нажав кнопку [Вставить Функцию] на панели инструментов и выбрав требуемую функцию max в окне Вставить Функцию.

3. В появившиеся в рабочей области маркеры-шаблоны этой функции вставьте заданную последовательность чисел: 25, 38, 10, 70.

4. Определите максимум указанной последовательности чисел, нажав знак равенства на панели Калькулятор, – искомый результат отобразится на экране (рис. 76).

5. Выполните аналогичные действия для нахождения минимального числа в заданной последовательности чисел.

Результат определения экстремумов представлен на рис. 76.

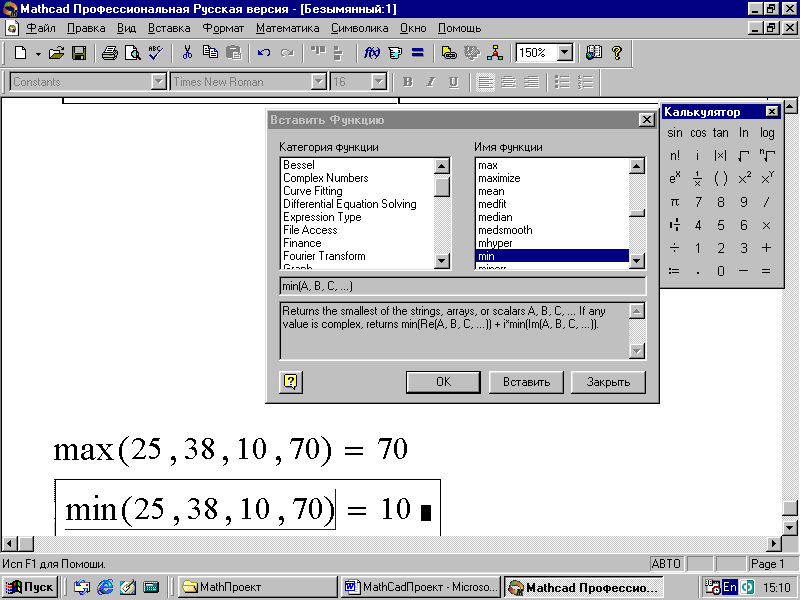
Рис. 76. Определение экстремумов последовательности чисел

Пример 47. Найти максимум следующей функции одной переменной: f(x)=-x²-x-1,– предварительно построив ее график.

1. Установив курсор и, вызвав панель Калькулятор, наберите заданную функцию.

2. Постройте график функции, используя панель Графики (рис. 77).

3. Задайте начальное значение х, например х=0.

4. Найдите максимум заданной функции f(x), воспользовавшись встроенной функцией maximize. Алгоритм и результат решения представлены на экране (рис. 77).

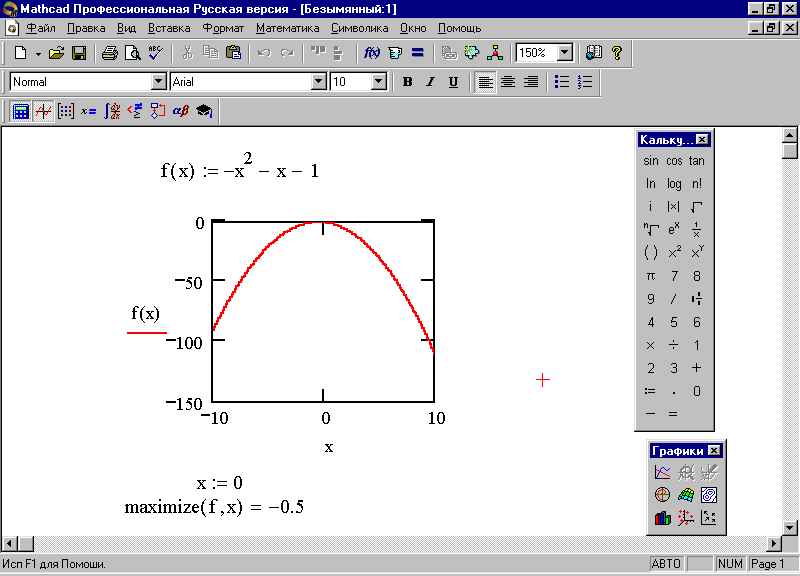
Рис. 77. Нахождение максимума функции одной переменной

Пример 48. Найти максимум следующей функции двух переменных:

.

1. Установив курсор и вызвав панель Калькулятор, наберите заданную функцию.

2. Найдите максимум заданной функции f(x,y), воспользовавшись встроенной функцией maximize. Алгоритм и результат представлены на экране (рис. 78).

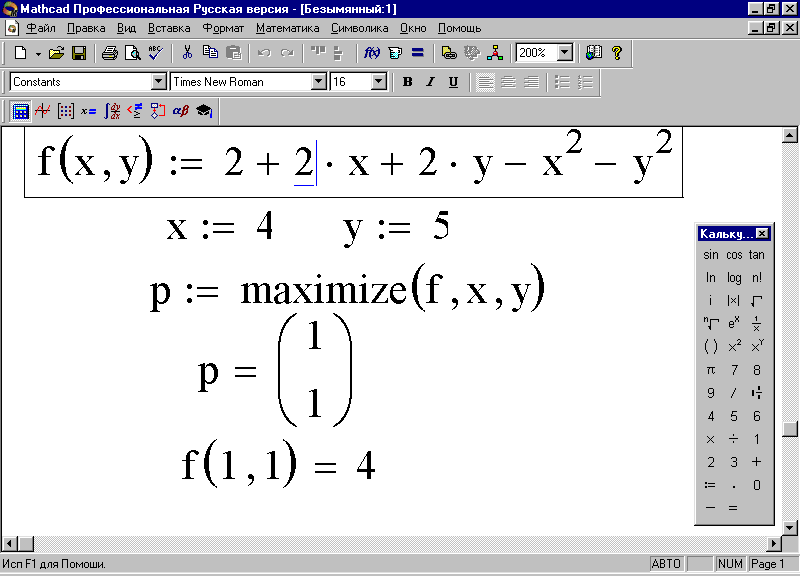
Рис. 78. Нахождение экстремума функции

15. Экстремум в экономических задачах

Пример 49. Выпуск продукции предприятием в денежном выражении по кварталам года составил соответственно: В1, В2, В3, В4 млн. руб. Вычислить годовой выпуск продукции, а также определить, в каком квартале выпуск был наибольшим.

Очевидно, что годовой выпуск продукции будет равен В1+В2+В3+В4, и мы имеем арифметическое выражение, которое требуется вычислить.

1. Выведите на экран панель Калькулятор.

2. Установите курсор в нужное место экрана.

3. Наберите значения переменных (произвольные), а затем требуемое выражение В:=В1+В2+В3+В4, после чего вычислите его, набрав символ В и нажав знак равенства, – результат вычисления появится на экране (рис. 79).

4. Воспользуйтесь встроенной функцией max для нахождения максимального выпуска, выбрав ее в окне Вставить Функцию, которое появляется после нажатия соответствующей кнопки [Вставить Функцию]на панели инструментов.

Алгоритм и результат решения представлен на рис. 79.

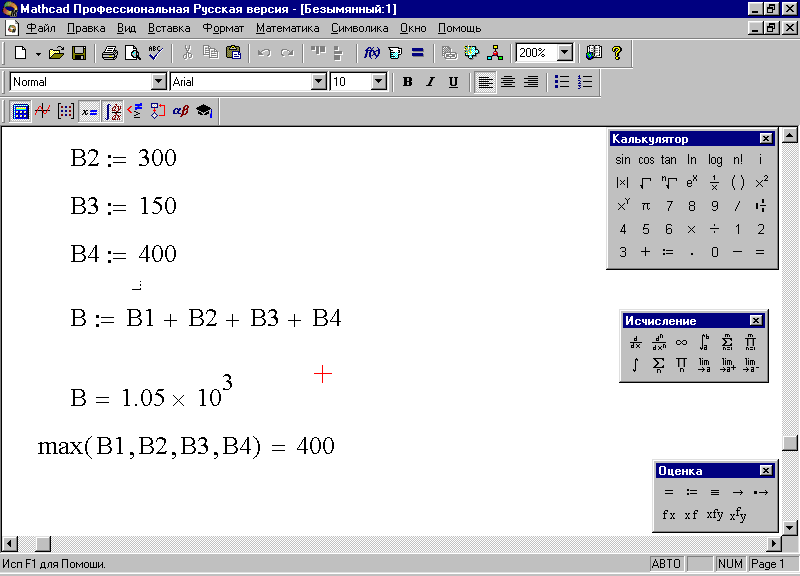
Рис. 79. Вычисление годового и максимального выпуска

Пример 50. Имеются данные о Всероссийской переписи населения 1897г. Согласно этим данным известно количество проживающих в каждой из пяти губерний Белоруссии: Гродненской, Витебской, Виленской, Минской и Могилёвской. Требуется вычислить общее количество жителей в Беларуси в тот период, а также определить, в какой области проживало минимальное количество жителей.

Введем условные обозначения. Пусть количество жителей, проживающих в каждой из губерний, обозначены К₁, К₂, К₃, К₄, К₅. Тогда общее количество жителей (К) определяется по формуле: К=К₁+К₂+К₃+К₄+К₅. Имеем выражение, алгоритм реализации которого аналогичен приведенному в предыдущем примере. Так же, как и в предыдущем примере, следует определить минимальное значение.

Пример 51. Потребность цеха в поставляемых ему в данный плановый период изделий составила X₁, Х₂, ..., Х_n, в другой плановый период соста­вила Y₁, Y₂, ..., Y_n. Определить потребность цеха в поставляемых изделиях за оба плановых периода по формуле S_i=Х_i+Y_i. Найти отклонения поставок второго планового периода от первого по формуле: R_i=X_i-Y_i (i=1,2,…,n). Определить также наименьшее отклонение.

В первом случае мы имеем сумму двух векторов, а во втором разность этих же векторов, то есть имеем задачу на сложение и вычитание векторов. Кроме того, следует также найти минимальное отклонение, руководствуясь ранее рассмотренным алгоритмом.

Пример 52. Выпуск продукции предприятием в отчетном квартале по месяцам распределился следующим образом: В₁, B₂, B₃. Найти среднемесячный выпуск и отклонение от него для каждого месяца. Определить также, в каком месяце отклонение было наименьшим.

Задача сводится к следующему: имеется вектор выпуска: B = (B₁, В₂, B_З). Требуется найти сумму элементов вектора и разделить её на 3. Затем вычислить отклонение для каждого месяца от найденного среднего и среди вычисленных отклонений найти наименьшее по выше рассмотренному алгоритму.