2.14. Нахождение производных и интегралов
Пример 43. Найти первую и вторую производные следующей функции: 25+35х+10х2.
1. Для нахождения производной вызовите на экран панели: Калькулятор, Исчисление, Символика.
2. Установите курсор в нужное место экрана и выберите на панели Исчисление знак производной.
3. В появившихся на экране шаблонах производной наберите заданную функцию 25+35х+10х2 и переменную х.
4. Определите производную, нажав на панели Символика символ со стрелкой, то есть – знак [Символическое Вычисление]. На экране появится искомый результат (рис. 70).
5. Для нахождения второй производной используются те же панели, и аналогичный алгоритм вычисления. Отличие лишь в том, что на панели Исчисление следует выбрать знак второй производной.
Результат представлен на том же экране (рис. 70).
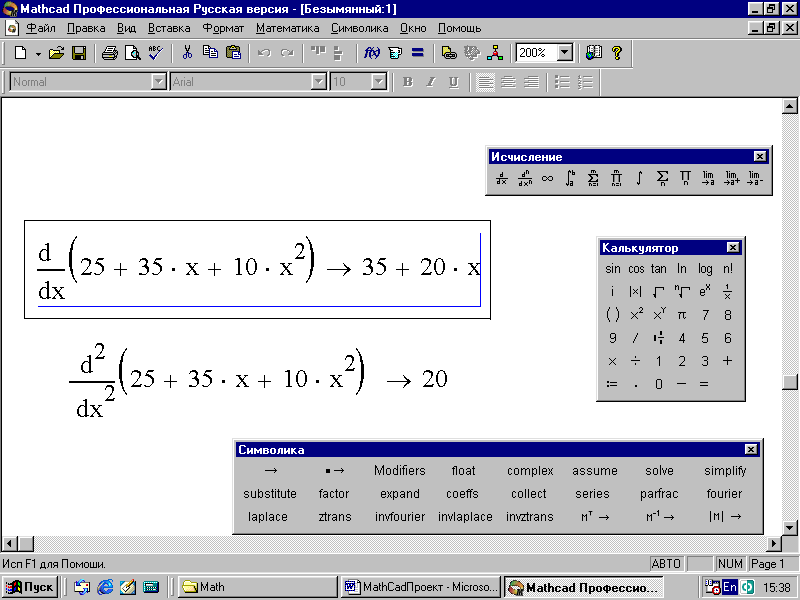
Рис. 70. Вычисление первой и второй производных
Для записи выражения с интегралом
используется кнопка –
[Определенный Интеграл] на панели
Исчисление. Нажатие этой кнопки
вызывает на экран шаблон интеграла.
После чего с клавиатуры надо в помеченные
позиции-маркеры шаблона ввести пределы
интегрирования, подынтегральную функцию
и переменную интегрирования.
Чтобы вычислить интеграл численно, надо
нажать на панели Калькулятор знак
равенства =. А для символьного вычисления
– кнопку
[Символическое Вычисление] в панели
Символика. Для завершения вычисления
надо щелкнуть по рабочему документу
вне выделяющей рамки. Вычисленное
значение интеграла будет отображено в
рабочем документе справа от стрелки.
Пример 44. Вычислить определенный интеграл в пределах [2;4] следующей функции: 25+35*х+10*х2 в численном и символьном виде.
1. Для записи выражения с интегралом вызовите панель Исчисление (рис. 71).
Рис. 71. Панель Исчисление
2. Установите курсор в нужное место на экране и активизируйте знак определенного интеграла на панели Исчисление.
3. Укажите в полях соответствующих шаблонов появившегося знака интеграла: пределы интегрирования, подынтегральную функцию и переменную, по которой производится интегрирование, – вызвав для этого панель Калькулятор.
4. Для получения результата интегрирования наберите знак равенства на панели Калькулятор – на экране появится искомый результат (рис. 72).
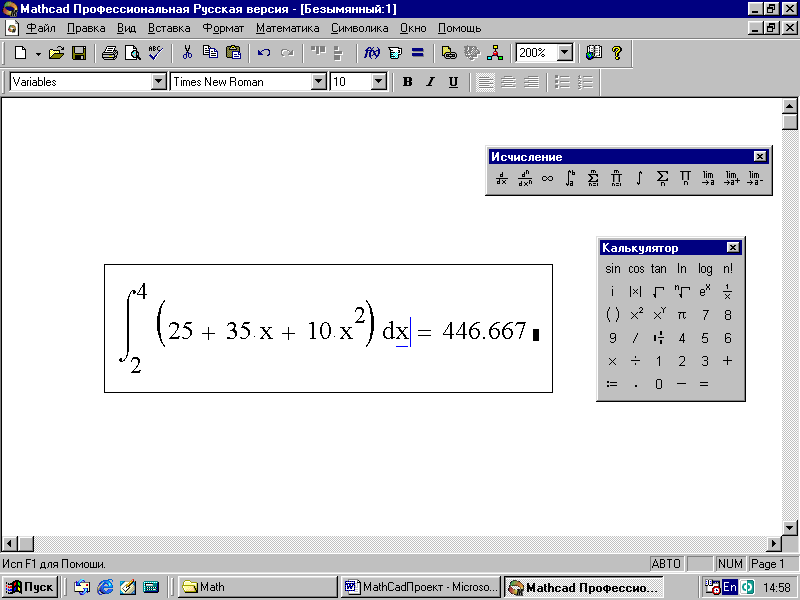
Рис. 72. Пример численного вычисления интеграла
5. Для символьного вычисления этого же интеграла вызовите панель Символика, и на ней в том же выражении вместо ранее набранного знака равенства выберите знак символьного вычисления (стрелку). Результат такого вычисления появится на экране (рис. 73).
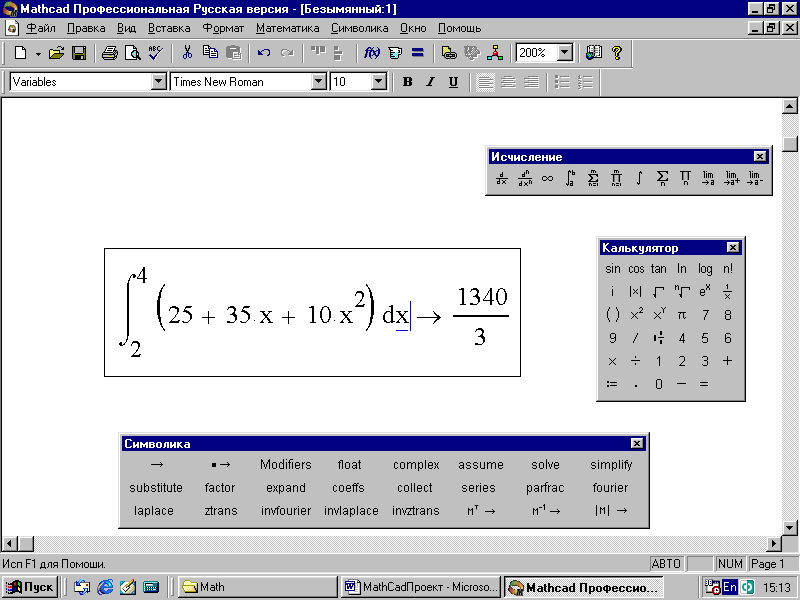
Рис. 73 . Пример символьного вычисления интеграла
Пример 45. Вычислить неопределенный интеграл следующей функции:
1. Установите курсор, вызовите панель Калькулятор и наберите подынтегральное выражение (рис. 74).
2. Окружив набранное выражение выделяющей рамкой, скопируйте его в буфер, чтобы затем его вставить под знак интеграла.
3. Вызовите панель Исчисление и, воспользовавшись этой панелью, вставьте знак неопределенного интеграла.
4. Вставьте из буфера подынтегральное выражение под знак интеграла и наберите переменную x, по которой производится интегрирование.
5. Вызовите панель Оценка.
6. Выделите всю формулу выделяющей рамкой и вычислите неопределенный интеграл, воспользовавшись кнопкой [Символическое Вычисление] на панели Оценка – результат вычисления появится на экране (рис. 73).
Можно поступить и несколько иначе: набрать заданную функцию , а затем под знаком интеграла набрать f(x) (рис. 74).
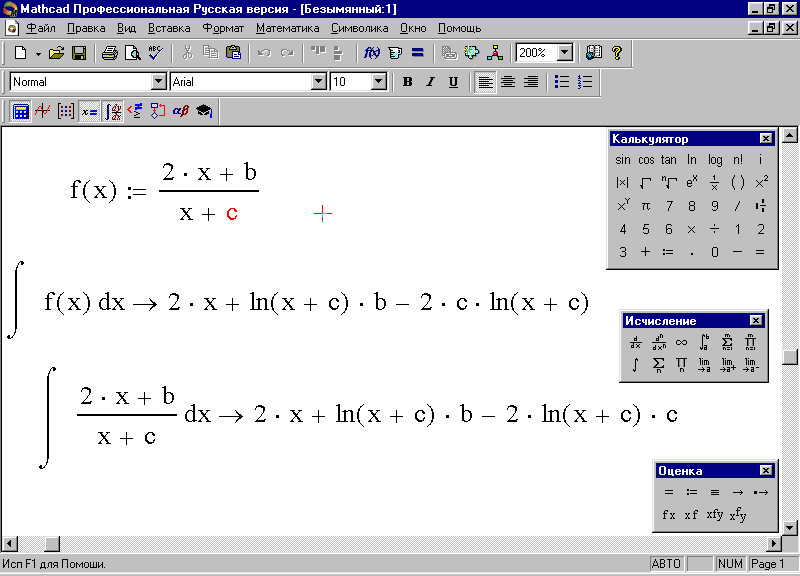
Рис. 74. Нахождение неопределенного интеграла