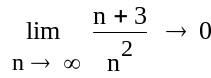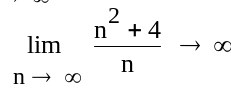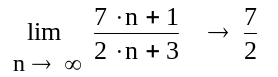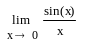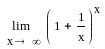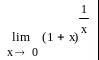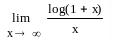1. Решение системы нелинейных уравнений графически

1. Вызовите панель Калькулятор и запишите зависимость одной переменной от другой в каждом из уравнений системы: F(x):= cos(x-1)-0.5; f(y):=y-cos(y)-3.

2. Постройте графики функций, пользуясь панелью Графики и правилами построения графиков. На экране появится результат, представленный на рис. 63.

3. Корнями системы уравнений будут координаты точки пересечения двух графиков. Найдите эту точку с помощью команды След, пользуясь правилами трассировки (рис. 63).

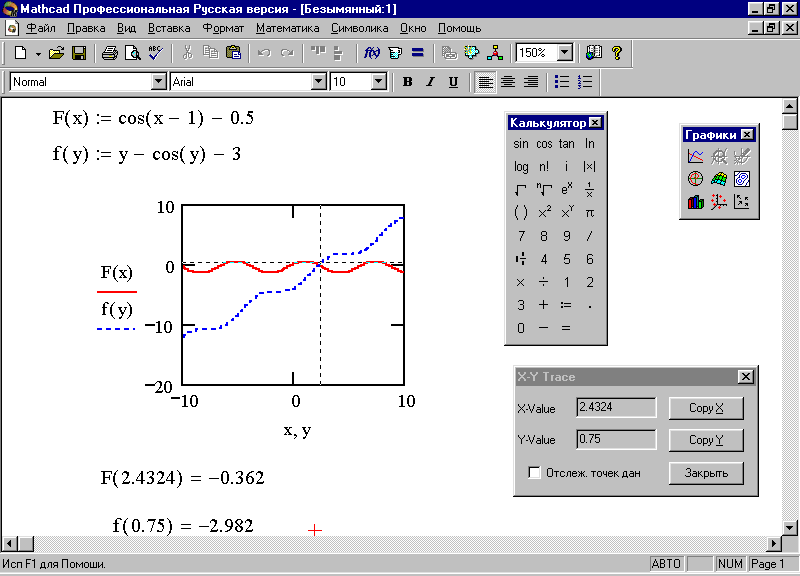
Рис. 63. Графики функций f(y) и F(х) в одних координатных осях

2. Решение системы нелинейных уравнений с помощью

given-find и given-minerr

Функция minerr(x, у, ...) – возвращает значения х, у, ..., – решения, наиболее близкие к решению системы уравнений. Здесь х, у, ... – скалярные переменные, значение которых определяются в системе уравнений. Если определяется одно неизвестное, то функция мinerr(x,у, ...) возвращает скаляр; в противном случае она возвращает вектор, первым элементом которого является искомое значение неизвестного x, вторым — y и т.д. Перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной и ключевое слово given. Если система имеет несколько решений, то нужное определяется заданным начальным приближением.

1. Задайте начальные значения переменным x и y, воспользовавшись панелью Калькулятор х:=3.3 у:=1.2.

2. Запишите служебное слово given.

3. Запишите систему уравнений, используя при наборе знака равенства в уравнениях соответствующий знак на панели Логические

given

c os(x - 1)= 0.5

у - cos(y) = 3

minerr(x, у) =

4. В конце этого блока запишите функцию minerr (рис. 63):

5. Аналогично выполните решение с использованием given и find (рис. 64).

6. Произведите проверку решения, и вы получите значения корня (рис. 65). Значит, решение c учетом заданной точности найдено верно.

Рис. 64. Решение системы нелинейных уравнений с помощью given и minerr

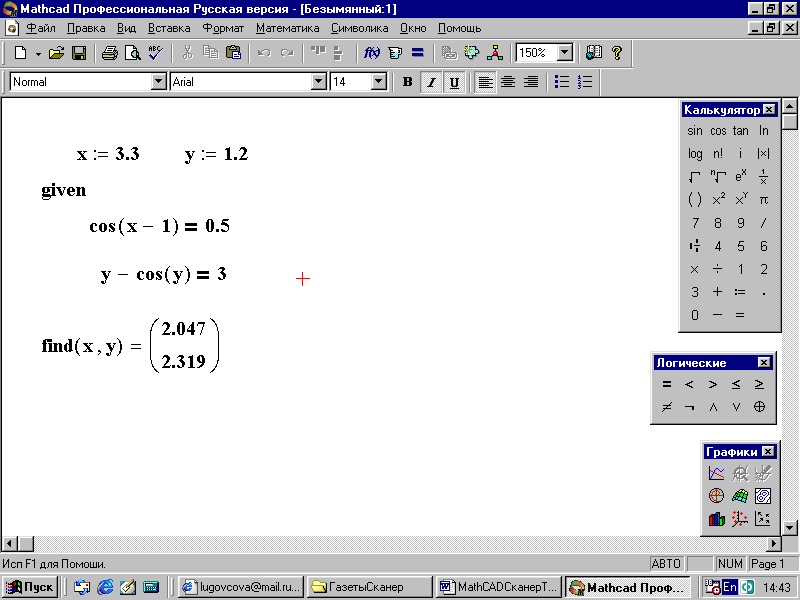
Рис. 65. Решение системы нелинейных уравнений с использованием given и find

П ример 40. Решить систему уравнений:

2x+3y=10;

x+4(y+log(y))=5.

1. Выведите на экран панели: Калькулятор и Логические.

2. Установите курсор и наберите начальные значения переменных: x:=0 и y:=1, используя панель Калькулятор.

3. Установите курсор под набранной информацией и наберите служебное слово given.

2. Установите курсор и наберите систему уравнений, используя знак равенства, изображенный на панели Логические (!).

3. Установите курсор и, используя функцию find, наберите find (x,y) = (здесь следует набрать обычный знак равенства) – результат появится на экране (рис. 66).

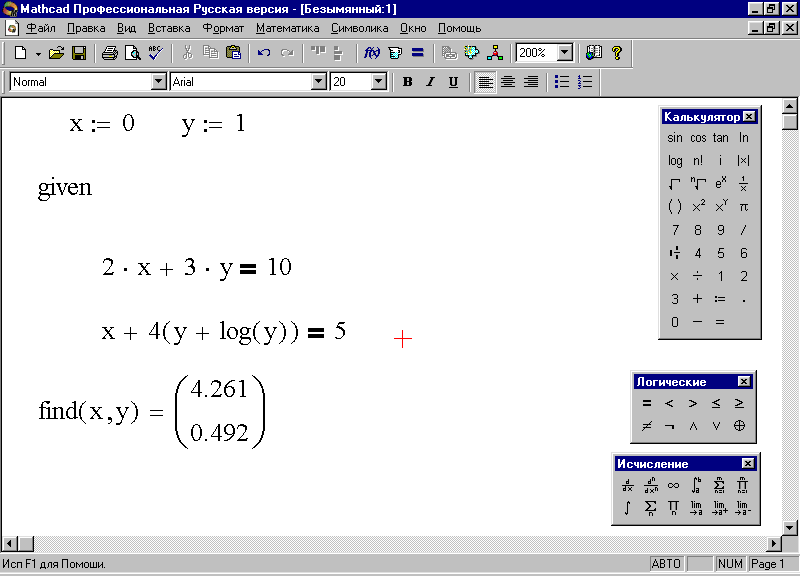
Рис. 66. Решение системы линейных уравнений

2.13. Нахождение пределов последовательностей и функций

Для нахождения пределов используются панели: Исчисление, Калькулятор, Символика или Оценка (рис. 67).

Рис. 67. Панели, используемые для нахождения пределов

Пример. 41. Найти пределы следующих последовательностей:

1. Активизируйте панели: Калькулятор, Исчисление, Оценка.

2. Установите курсор в рабочей области и, используя панель Исчисление, наберите знак предела (lim).

3. Укажите конкретную последовательность и пределы, используя панель Калькулятор.

4. Определите искомый предел, нажав кнопку со стрелкой [Символическое Вычисление] на панели Оценка и клавишу ввода – на экране появится искомый результат (рис. 68).

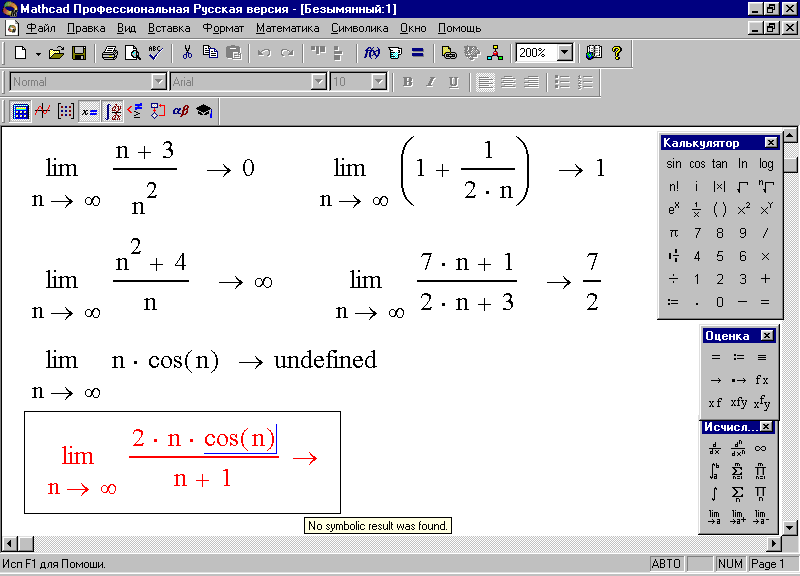
Рис. 68. Нахождение пределов последовательностей

Пример. 42. Найти пределы следующих функций:

1. Поскольку первые три предела относятся к замечательным пределам, и их результат известен заранее – это соответственно: 1, е, е, – то мы лишь проверим предполагаемый результат. Для этого наберите их условия, используя панели: Калькулятор и Исчисление, а затем найдите пределы, используя на панели Символика оператор [Символьное Вычисление], представляющий собой стрелку.

2. Что же касается нахождения остальных пределов, то наберите их условия и произведите вычисления, используя выше указанные панели. Общий результат представлен на рис 69.

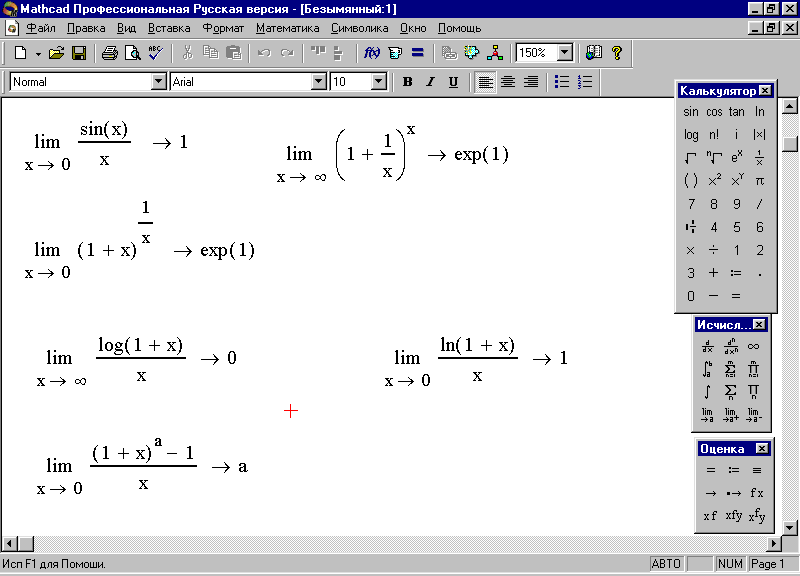
Рис. 69. Нахождение пределов функций