2.16. Нелинейные уравнения и системы

Нелинейные уравнения и системы часто не имеют аналитических решений и решаются графическими или численными методами с заданной точностью вычислений.

Пакет MathCAD имеет функцию root (f(x),x), решающую одно уравнение с одним неизвестным. Поиск корня уравнения осуществляется итерационным методом, причем перед этим нужно задать начальное значение х. Если уравнение имеет несколько корней, то их можно найти последовательно, используя функцию root при различных начальных значениях х.

Если в MathCAD необходимо найти решение системы уравнений, то следует задать блок уравнений, который должен иметь следующую структуру:

Given – служебное слово, которое отмечает начало блока системы уравнений

Уравнения

Ограничительные условия

Find(х,у,…) или minerr(х,у,…) – функции для решения системы уравнений.

Функция find (v1,v2,...vn) – возвращает значение одной или нескольких переменных, отвечающих точному решению.

Функция minerr (v1,v2,...vn) – возвращает значение одной или нескольких переменных, отвечающих приближенному решению с минимальной среднеквадратической погрешностью, даже в том случае, когда функция Find не находит решения. При использовании minerr рекомендуется проводить проверку найденных решений.

При решении уравнений используются панели инструментов: Калькулятор, Графики, Логические.

Пример 36. Решить следующее уравнение 4x-2sin(3x)log(5x)=0.

1. Для записи заданного уравнения выведите на экран панель Калькулятор.

2. Установите курсор на рабочей области и запишите уравнение в виде: .

3. Подведите курсор к переменной x и выполните команду Символика>Переменная>Разрешить – на экране появится результат (рис. 56).

4. Решите это же уравнение самостоятельно, используя функции: root, Given и Find – и вы получите тот же результат.

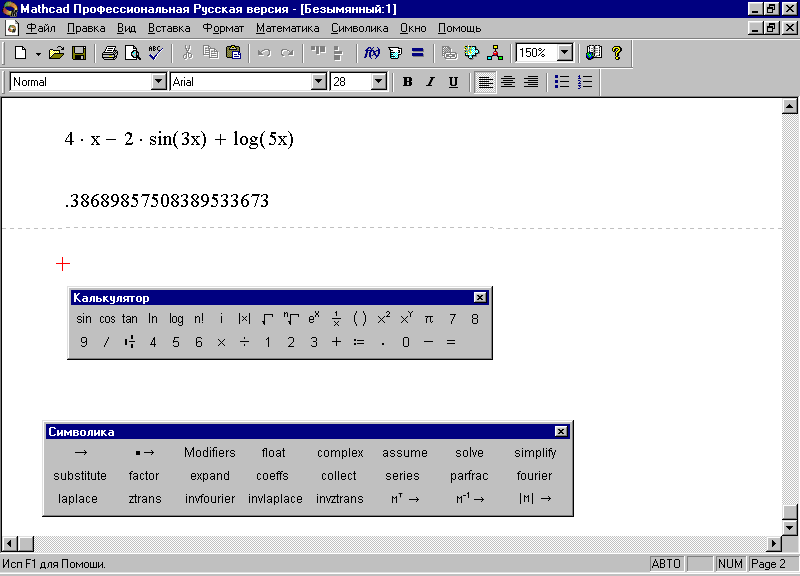
Рис. 56. Решение линейного уравнения

Пример 37. Решить квадратное уравнение одной переменной х²+2х=20.

1. Для записи этого уравнения выведите на экран панель Калькулятор командой Вид>Панели>Вычисления.

2. Приведите уравнение к виду f(x)=0 и наберите его, используя панель Калькулятор, х²+2х-20.

3. Подведите курсор к переменной x и выполните команду Символика >Переменные>Разрешить – на экране увидите результат, представленный на рис. 57.

Рис. 57. Решение уравнения второго порядка

4. Решите это же уравнение с помощью функции root – результат будет аналогичным (рис. 58).

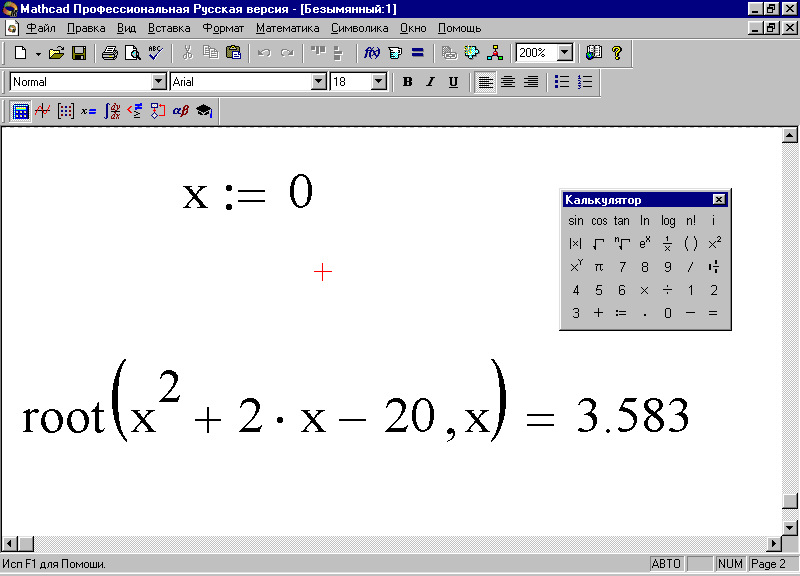
Рис. 58. Решение уравнения с использованием функции Root

Пример 38. Решить нелинейное уравнение x*lg(x+1)=1 с точностью до 0.1. Решение выполнить графически, а также с помощью функции root.

1. Запишите данное уравнение как функцию f(x):=x*Iog(x+ 1)-1 в рабочем окне документа, используя панель Калькулятор.

2. Начните решать данное уравнение графически:

• установите курсор на рабочем листе;

• выберите из меню Вставка команду График (или нажмите комбинации клавиш [Shift+2]) – появится шаблон графика в декартовых координатах;

• введите в метку на оси X независимую переменную – х, а на оси Y функцию –f(x).

• щелкните мышью вне графика – и на экране появится график функции f(x)= х * log(x + 1) - 1 (рис. 59).

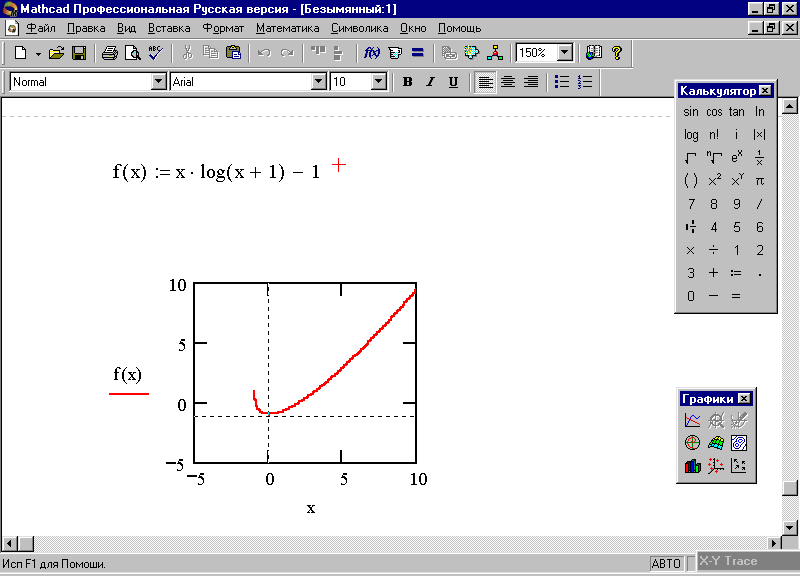
Рис.59. График функции f(x) = х *log(x +1) –1

3. При графическом решении уравнения его корнями будут являться точки пересечения графика функции с осью ОХ. Для определения координат точек пересечения графика с осью воспользуйтесь трассировкой:

• щелкните по графику правой клавишей мыши;

• в появившемся меню выберите команду След – появится окно X-Y Trace (Трассировка декартова графика), отображенное на рис. 59;

• установите указатель мыши на кривой, нажмите левую кнопку и, не отпуская ее, переместите указатель вдоль кривой. В диалоговом окне X-Y Trace по мере движения по кривой будут определяться различные координаты положения указателя на кривой (рис. 60).

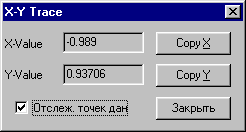
Рис. 60. Окно Х-Y Trace

• найдя значение по оси Х, при котором значение по оси Y удовлетворяет заданной точности (рис. 61), скопируйте данные в буфер обмена кнопками [Copy X] и [Copy Y], расположив данные под графиком.

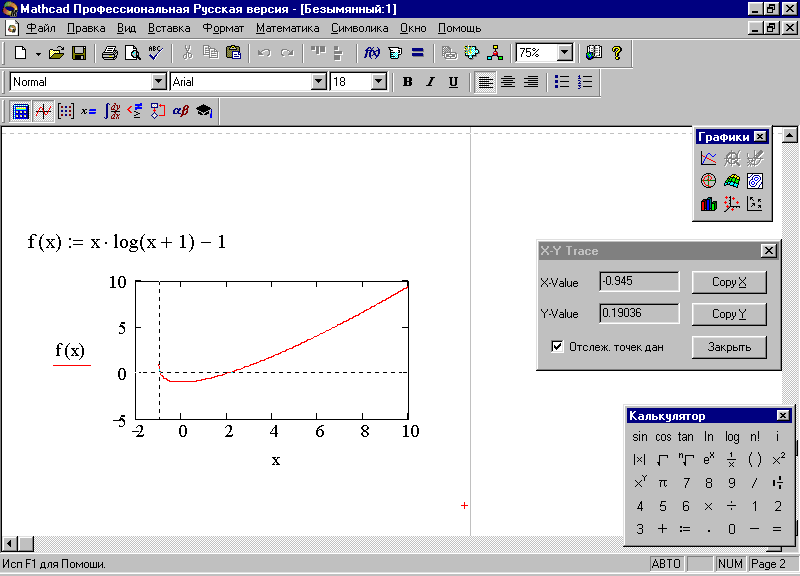
Рис. 61. Решения нелинейного уравнения с помощью трассировки

4. Функция root(f(x),х) находит корень уравнения с одним неизвестным. Она возвращает значение х, при котором функция root(f(x),х) равна нулю. Использование функции root требует предварительного задания начального значения корней (приближения). Если исследуемая функция имеет несколько корней, то найденный корень будет зависеть от начального приближения. Если оно расположено близко к локальному экстремуму функции f(x), то функция root может не найти корня, либо найденный корень будет далек от начального приближения.

Решите заданное нелинейное уравнение с помощью функции root. Для чего задайте приближенные начальные значения независимой переменной х и воспользуйтесь функцией root(f(x),x):

х:=-0.9

root(f(x),x) = -0.918

х:=2.05

root(f(x),x) = 2.059

Результат представлен на рис. 62.

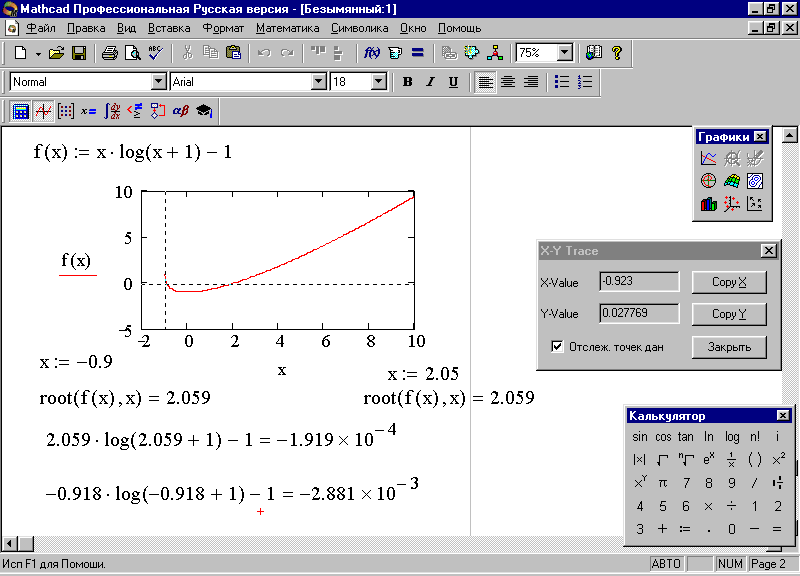
Рис. 62. Решение системы уравнений с использованием функции root

5. Произведите проверку значений, полученных графическим методом, и сравните их с результатами вычисления с помощью функции root(f(x),x), подставляя полученные значения корней в уравнение:

2.059 * log(2.059+ 1) = 1; -0.918 * log(-0.918+ 1) = 1.

Проверка показала (рис. 61), что решения, найденные двумя методами, совпадают с учетом заданной точности.

Пример 39. Решить с точностью до 0.001 следующую систему нелинейных уравнений:

c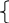 os(х-1) = 0.5;

y – cos y = 3.

Решение выполнить графически, а также с помощью given и find или given и minner.

Алгоритм реализации рассматривается далее.