2.10.5. Решение системы линейных алгебраических уравнений с помощью метода Гаусса
1 . Запишите матрицы А и В (столбец свободных членов):
1.71 -0.8 1.44 -0.7 1.35
А := 0.64 -0.85 -0.43 0.88 В := 0.7
0.38 1.42 0.63 -1.55 0.28
0.83 -0.6 0.58 -1.22 - 0.47
2. Сформируйте расширенную матрицу, использовав предназначенную для этого функцию: C:=augment(A,B)
1 .71 -0.8 1.44 -0.7 1.35
С = 0.64 -0.85 -0.43 0.88 0.7
0.38 1.42 0.63 -1.55 0.28
0.83 -0.6 0.58 -1.22 -0.47
3. Примените метод Гаусса, сформировав единичную матрицу из расширенной, использовав предназначенную для этого функцию: D:= rref(C)
1 0 0 0 1.091
D = 0 1 0 0 0.767
0 0 1 0 0.563
0 0 0 1 1.018
4. Выделите с помощью функции submatrix блок из матрицы D x:=submatrix (D,0,3,4,4) – и вы получите искомый результат (рис. 53):
1.091
X= 0.767
0.563
1.018
где D – название матрицы, из которой находится выделяемый блок,
0 – начальный номер строки выделяемого блока,
3 – конечный номер строки выделяемого блока (нумерация начинается с нуля),
4 – начальный номер столбца выделяемого блока,
4 – конечный номер столбца, выделяемого блока.
5. Выполните анализ всех полученных результатов. И вы увидите, что, решая систему линейных алгебраических уравнений пятью различными способами, вы получили один и тот же ответ, что говорит о правильности найденных результатов.
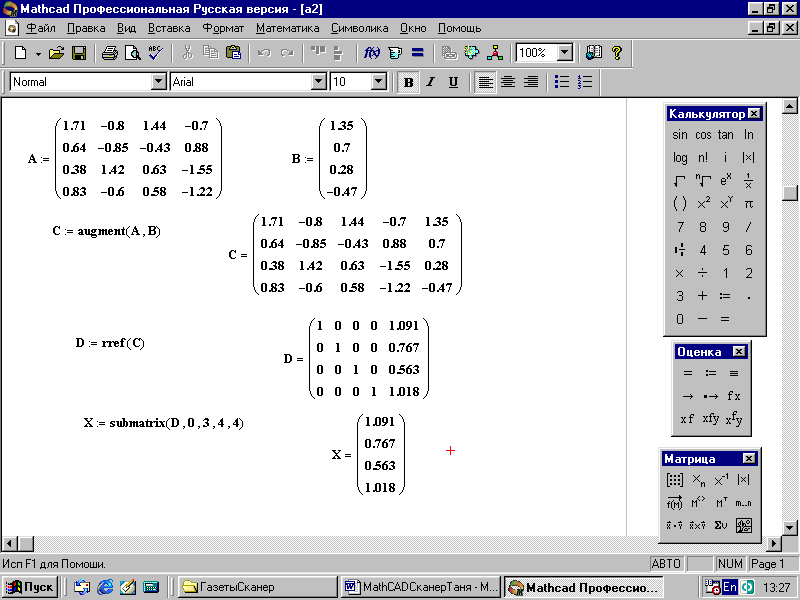
Рис. 53. Решение системы линейных уравнений методом Гаусса
2.11. Линейные уравнения и системы в экономических задачах
Пример 34. Предприятие выпускает продукцию трех видов: А, В и С. Выпуск продукции ограничен запасом ресурсов. Исходные данные приведены в таблице 5 .
Таблица 5. Выпуск предприятия
-
Ресурсы
Запас ресурса
Нормы затрат на 1 продукции
А
В
С
Сырье, кг
24
5
7
4
Материалы, кг
75
10
5
20
Оборудование, ед
10
5
2
1
Определить, какое количество продукции каждого вида может выпустить предприятие в этих условиях.
Имеем систему трех уравнений с тремя неизвестными. Решим ее методом обратной матрицы (рис. 54).
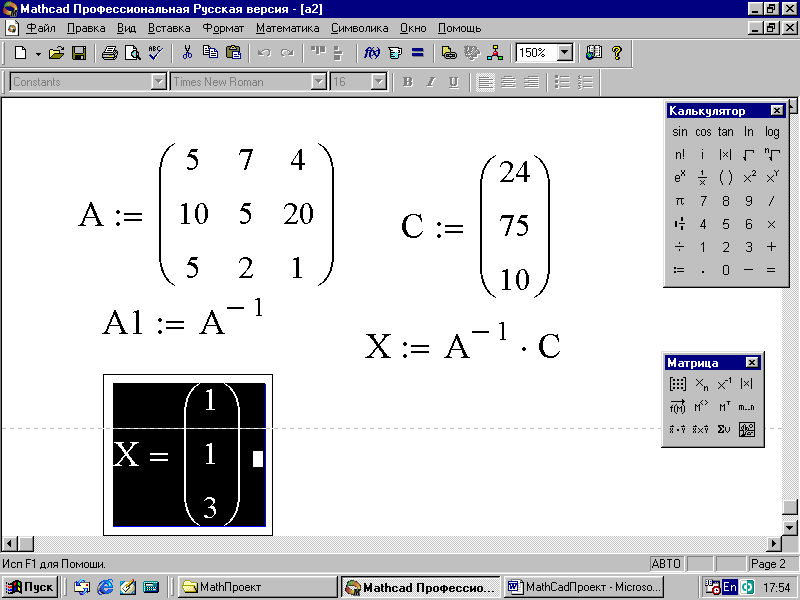
Рис. 54. Определение выпуска изделий при заданных ограничениях
Пример 35. На двух молочных заводах производится два одинаковых вида товаров: молоко и творог. Сведения об удельной трудоемкости производства этих товаров и общих затратах на них приведены в таблице 6.
Удельная трудоемкость Таблица 6
Наименование товара |
Удельная трудоемкость, чел./час. |
Общие затраты, чел./час. |
|
Завод 1 |
Завод 2 |
||
Молоко |
0.5 |
1.1 |
200 |
Творог |
0.1 |
1.7 |
300 |
Каков должен быть выпуск молока и творога на каждом предприятии, если общие трудозатраты на каждом из них должны равняться: по молоку 200, а по творогу 300.
Задача сводится к решению систем уравнений с неизвестными переменными: х1 – количество молока и х2 – количество творога. Решить её можно, используя функцию Find (рис. 55).
Задайте произвольные начальные значения переменным х1 и х2, например: х1=0 и х2=0.
Наберите служебное слово Given.
Запишите уравнения системы.
Воспользуйтесь встроенной функцией Find для нахождения корней системы (рис. 55).
Рис. 55. Определение выпуска молочных товаров