2.10.2. Решение системы линейных алгебраических уравнений с помощью функции lsolve(m,V)
Функция lsolve(M,v) – возвращает вектор х решения системы линейных уравнений M•x=v, где v – вектор правых частей системы линейных уравнений.
1. Запишите матрицу A, которая будет состоять из коэффициентов, стоящих перед неизвестными x1, х2, хЗ, х4:
1
.71
-0.8 1.44 -0.7
А:= 0.64 -0.85 -0.43 0,88
0.38 1.42 0.63 -1.55
0.83 -0.6 0.58 -1.22
2. Запишите матрицу В, которая будет состоять из столбца свободных членов:
1
.35
В:= 0.7
0.28
-0.47
3. Решите систему с помощью lsolve(M,v), записав x:=lsolve(A,B), и вы получите искомый результат:
1
.091
x = 0.767
0.563
1.018
Проверьте решение, вычислив выражение А•х-В, и вы получите нулевую матрицу, значит, вектор решений – х найден верно (рис. 48).
0
А • х – В = 0
0
0
Рис. 48. Решение системы нелинейных уравнений с использованием lsolve
2.10.3. Решение системы линейных алгебраических уравнений с помощью обратной матрицы
1. Запишите матрицы: А и В (столбец свободных членов):
1
.71
-0.8 1.44 -0.7 1.35
А:= 0.64 - 0.85 -0.43 0.88 В:= 0.7
0.38 1.42 0.63 -1.55 0.28
0.83 - 0.6 0.58 -1.22 -0.47
2. Решите систему: х:=А-1 • В, используя обратную матрицу:
1.091
x = 0.767
0.563
1.018
3 . Произведите проверку полученного решения по формуле А • х = В:
1.35
А • х = 0.7
0.28
-0.47
В результате проверки видно, что результат вычисления выражения A•x равен столбцу свободных членов, следовательно, решение найдено верно (рис. 49).
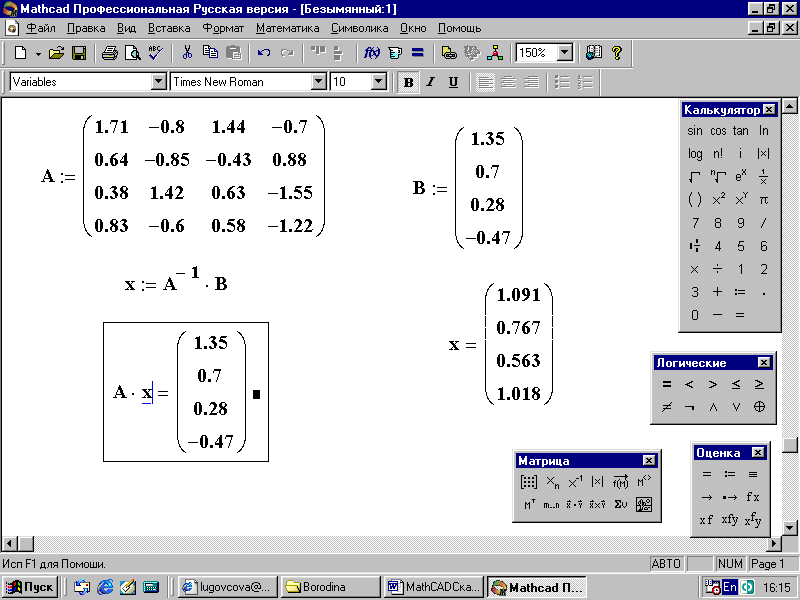
Рис. 49. Решение системы линейных уравнений с использованием обратной матрицы
2.10.4. Решение системы линейных алгебраических уравнений по формулам Крамера
Запишите матрицы А и В (столбец свободных членов)
1 .71 -0.8 1.44 -0.7
А:= 0.64 -0.85 -0.43 0.88
0.38 1.42 0.63 -1.55
0.83 -0.6 0.58 -1.22
1.35
В:= 0.7
0.28
-0.47
Вычислите определитель, составленный из элементов матрицы А (рис. 49):
DetA:=|A| DetA = -2.649.
Так как определитель матрицы А не равен нулю, то у системы имеется единственное решение.
Замените элементы первого столбца матрицы А на элементы матрицы В и вы получите матрицу А1:
1 .35 -0.8 1.44 -0.7
А1 := 0.7 -0.85 -0.43 0.88
0.28 1.42 0.63 -1.55
-0.47 -0.6 0.58 -1.22
4. Вычислите определитель полученной матрицы А1: DetА1 = -2.889 (рис. 50).
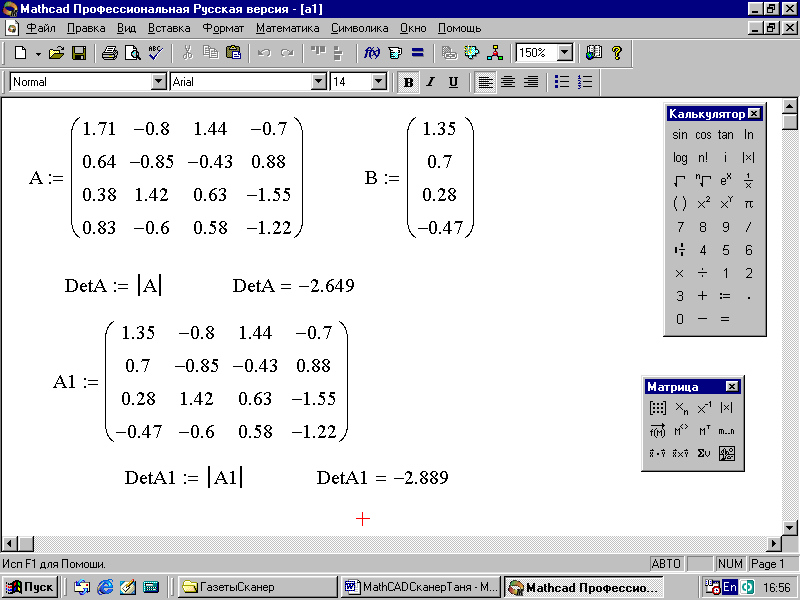
Рис. 50. Решение системы линейных уравнений по формулам Крамера (начало)
5. Замените элементы второго столбца матрицы А на элементы матрицы В и вы получите матрицу А2:
1 .71 1.35 1.44 -0.7
А2:= 0.64 0.7 -0.43 0.88
0.38 0.28 0.63 -1.55
0.83 -0.47 0.58 -1.22
6. Вычислите определитель вновь полученной матрицы А2: DetА2 =-2.031 (рис. 51).
7. Замените элементы третьего столбца матрицы А на элементы матрицы В и вы получите матрицу А3:
1 .71 -0.8 1.35 -0.7
А3:= 0.64 -0.85 0.7 0.88
0.38 1.42 0.28 -1.55
0.83 -0.6 -0.47 -1.22
8. Вычислите определитель полученной матрицы А3: DetA3 = -1.492 (рис. 51).
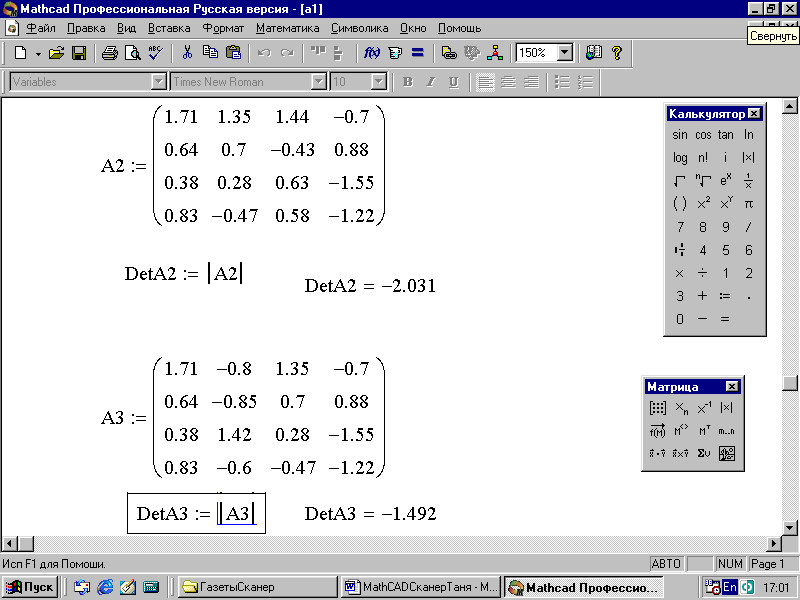
Рис. 51. Решение системы линейных уравнений по формулам Крамера (продолжение)
9. Замените элементы четвертого столбца матрицы А на элементы матрицы В и вы получите матрицу A4:
1 .71 -0.8 1.44 1.35
A4:= 0.64 -0.85 -0.43 0.7
0.38 1.42 0.63 0.28
0.83 -0.6 0.58 -0.47
10. Вычислите определитель полученной матрицы A4: DetA4 = -2.697 (рис. 52).
11. Найдите решение системы: x1, x2, хЗ, x4, – по формулам Крамера, разделив определители: DetА1, DetА2, DetА3, DetА4, – на определитель DetА. Получите: x1= 1.091, x2=0.767, x3=0.563, x4= 1.018 (рис. 52).
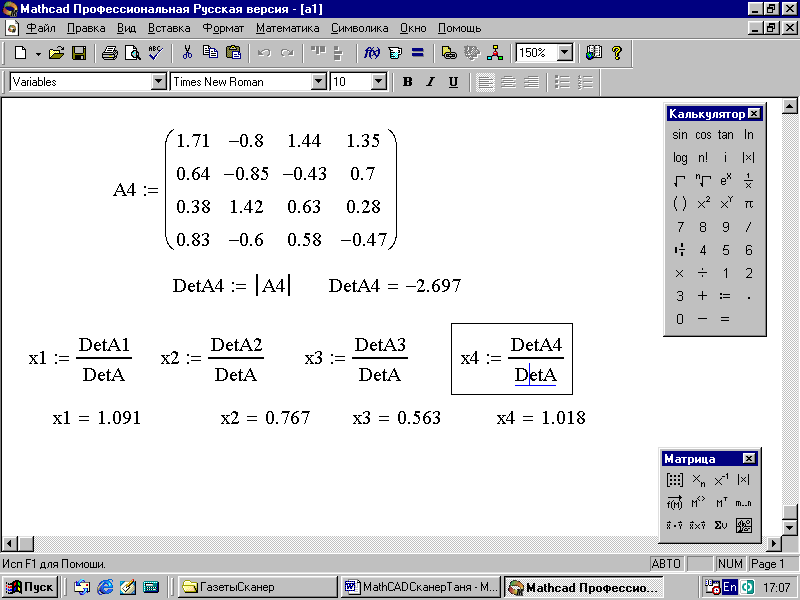
Рис. 52. Решение системы линейных уравнений по формулам Краммера (конец)