П ример 31. Решить систему линейных уравнений:
2х+3у=10;
х+10(у+5)=5;
взяв в качестве начальных приближений: х=0; y=1.
1.
Для записи системы уравнений выведите
панель Логические
(рис. 44) с помощью соответствующей кнопки
на панели Математика
.
Рис. 44. Панель Логические
2. Задайте начальные приближения: x:=0 y:=1.
3. Наберите на клавиатуре служебное слово Given.
4.
Введите последовательно оба уравнения
системы, используя кнопку
на панели Логические
(не путать
со знаком равно, который используется
для получения результата).
5. Для вычисления значений x и y наберите функцию Find(x,y)=. Знак равно ввести с клавиатуры, или с панели Калькулятор.
Алгоритм и результат представлены на рис. 45.
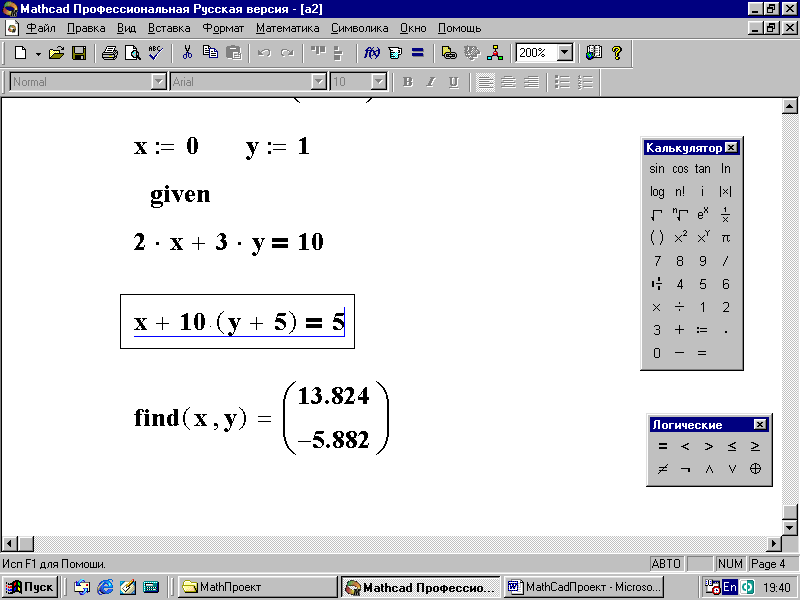
Рис. 45. Решение системы уравнений
Пример 32. Решить систему двух линейных алгебраических уравнений первого порядка:
2
x+3y=10;
x+y+log5=5.
1. Выведите на экран панели: Калькулятор и Логические.
2. Установите курсор и наберите произвольные начальные значения переменных, например: x:=0 и y:=1, используя панель Калькулятор.
3. Установите курсор под набранной информацией и наберите служебное слово Given.
2. Установите курсор под словом Given и наберите систему уравнений, используя знак равенства, изображенный на панели Логические (!).
3. Установите курсор и, используя функцию Find, наберите Find (x,y) = (здесь следует набрать обычный знак равенства) – на экране появится результат (рис. 46).
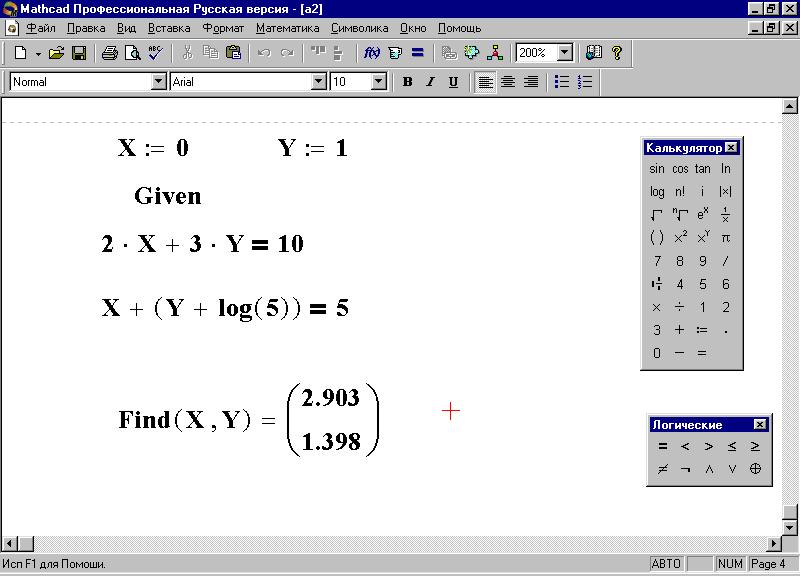
Рис. 46. Решение системы линейных уравнений
П
ример
33.
Решить следующую систему
четыре линейных алгебраических уравнений:
1 .71x1 - 0.8x2 + 1 .44x3 - 0.7x4 = 1 .35
0.64x1 - 0.85x2 - 0.43x3 + 0.88x4 = 0.7
0.38x1 + 1.42x2 + 0.63x3-1.55x4 = 0.28
0.83x1 - 0.6x2 + 0.58x3 - 1 .22x4 = -0.47
Решение выполнить несколькими способами:
с помощью Given и Find.
с помощью функции lsolve.
с помощью обратной матрицы.
по формулам Крамера.
методом Гаусса.
Алгоритмы реализации приведены ниже.
2.10.1. Решение системы линейных алгебраических уравнений с помощью Given и Find
Функция Find(x,у,...) – возвращает значения х, у, ..., удовлетворяющие ограничениям: равенствам и неравенствам, заданным в блоке решения уравнений Given. Число уравнений должно равняться количеству неизвестных х, у, ... Когда ищется одна неизвестная, то функция Find возвращает скаляр – иначе она возвращает вектор, первым элементом которого является искомое значение неизвестной х, вторым – у и т.д. Если система имеет несколько решений, то нужное решение будет определяться заданным начальным приближением. В этом случае перед использованием этой функции необходимо задать начальное приближение для каждой неизвестной.
Вызовите панели Калькулятор, Логические, Оценки.
Наберите слово Given.
Запишите в рабочей области систему уравнений (ограничений).
Найдите корни заданной системы, воспользовавшись функцией Find(x,у,...):
G
iven
1.71x1 – 0.8x2+ 1.44x3 – 0.7x4 = 1.35
0.64x1 – 0.85x2 – 0.43x3 + 0.88x4 = 0.7
0.38x1 + 1.42x2 + 0.63x3 – 1.55x4 = 0.28
0.83x1– 0.6x2 + 0.58x3 – 1.22x4 = - 0.47
Find(xl,x2,x3,x4) =
Так как система имеет более одного неизвестного, то ответ будет представлен в виде вектора, элементы которого есть соответственно искомые значения: xl, х2, хЗ, х4 (рис. 47).
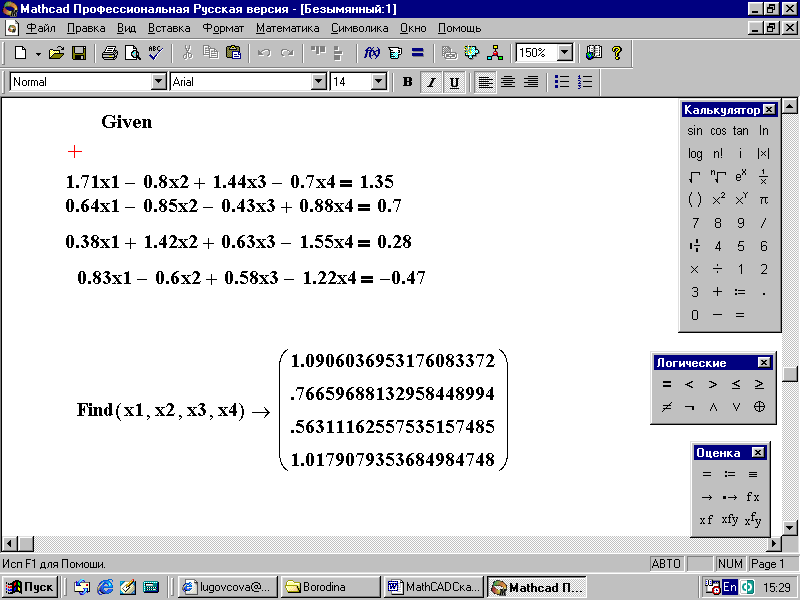
Рис. 47. Решение системы линейных уравнений с использованием Given и Find