Задача сводится к нахождению разности двух векторов X и y.

Пример 25. Имеются показатели деятельности колхоза о производстве сельскохозяйственной продукции: надоях молока, урожайности, укосах и т. д. В этом же хозяйстве собраны данные приехавшим статистиком, работавшим по специальной методике сбора информации.

Определить отклонение между данными колхоза и статистика по каждому показателю.

Введем следующие условные обозначения:

К₁, К₂,...К_n – показатели колхоза;

С₁, С₂,...С_n – показания статистика.

Имеем задачу на разность двух векторов.

Пример 26. На предприятии, работающем в три смены, электроэнергия должна расходоваться соответственно в количествах е1,е2,е3 кВт/час в каждую смену. За счёт внедрения рационализаторского предложения потребление электроэнергии снизилось на З%. Определить, на сколько кВт/час снизилось потребление электроэнергии в каждую смену?

Имеем трёхмерный вектор потребления электроэнергии по сменам Е=(е₁,е₂,е_З). Задача сводится к умножению этого вектора на число 3/100 (рис. 39).

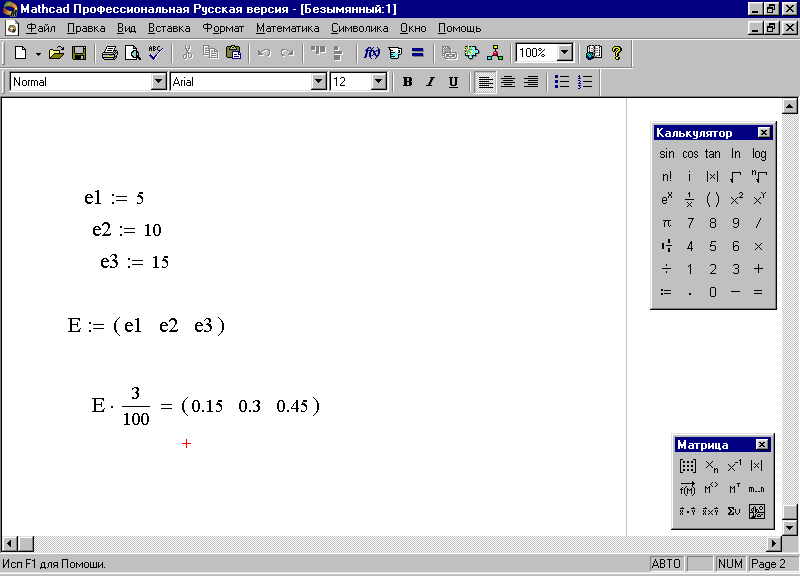
Рис. 39. Определение снижения потребления электроэнергии

Пример 27. В отчетном году валовой доход предприятия по кварталам года составил: С1, С2, С3, С4. Определить среднеквартальный валовой доход, а также отклонение среднеквартального валового дохода.

Имеем вектор поквартального валового дохода предприятия С=(С1, С2, С3, С4). Требуется найти сумму элементов этого вектора S=С1+С2+С3+С4 и разделить её на 4: SК=S/4. Из найденной суммы вычесть каждую компоненту вектора С: С1-SК, С2-SК, С3-SК, С4-SК.

Алгоритм и результат решения представлены на рис. 40.

Рис. 40. Определение среднеквартального дохода

Пример 28. Ткацкая фабрика выпустила хлопчатобумажные ткани пяти артикулов в количествах (метров): первый артикул – K₁, второй – K₂, третий – K₃, четвёртый – K₄, пятый – K₅. На эти ткани расходовано пряжи трёх сортов в количестве (м): первого сорта – P₁, второго – Р₂, третьего – Р₃. Определить С – количество метров пряжи, потраченное в среднем на 1 м ткани.

Имеем два вектора K=(К1,К2,К3,К4) и P=(Р1,Р2,Р3). Надо найти суммы их компонентов и одну разделить на другую:

C=	P1+P2+P3
	K1+K2+K3+K4+K5

Алгоритм и результат решения задачи представлены на рис 41.

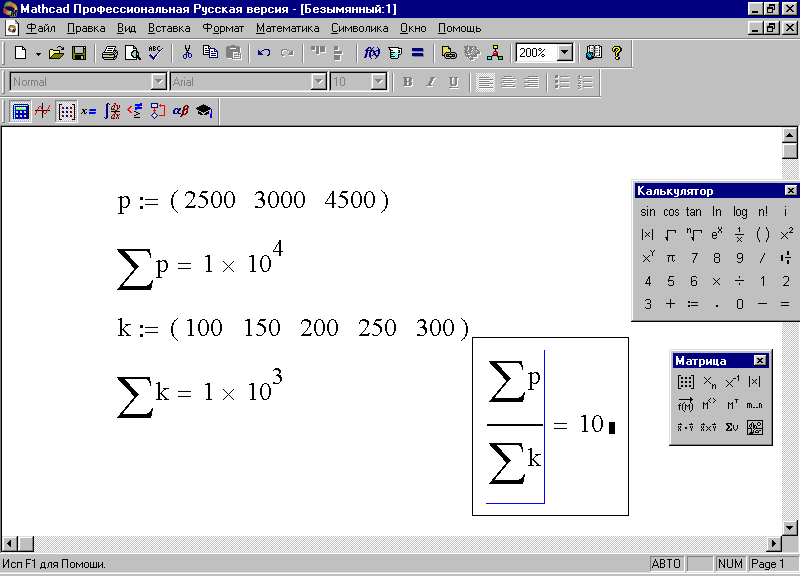
Рис. 41. Определение израсходованной пряжи на один метр ткани

Пример 29. Предприятие выпустило изделия n-видов в количествах К₁,К₂,.. .,К_n единиц, на которые использованы ресурсы на суммы: С₁,С₂,. .., С_n руб. соответственно. Определить P – общую сумму денег, затраченную на выпущенные изделия.

Имеем два вектора К и С. Требуется найти их скалярное произведение:

Алгоритм и результат решения задачи для вектора, имеющего четыре компоненты, представлены на рис 42.

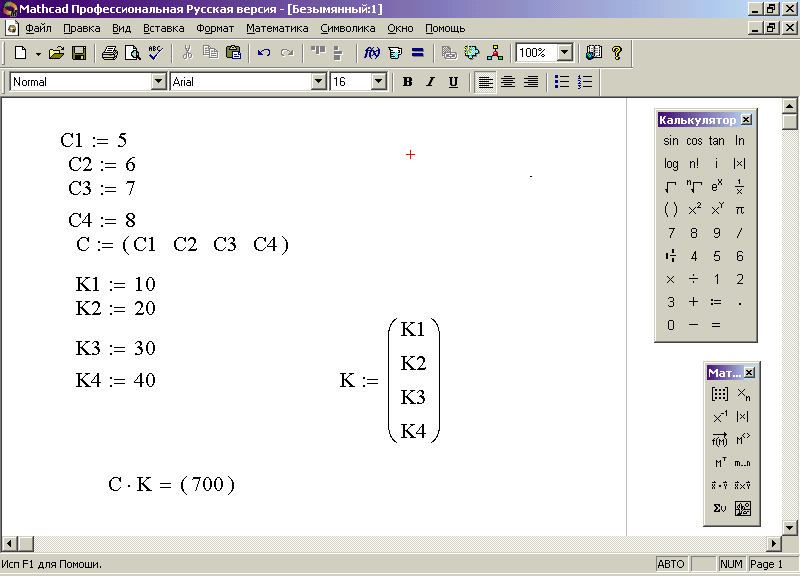
Рис. 42. Определение суммы, затраченной на ресурсы

2.10. Линейные уравнения и системы

Чтобы интерпретировать математические закономерности реальных явлений в экономике, формируют соответствующие им математические модели относительно одной или нескольких переменных. Широкое распространение в экономических исследованиях получили линейные модели. Большинство линейных моделей сводятся к линейным алгебраическим уравнениям (неравенствам) или системам. И их удобно решать средствами пакета MathCAD.

В пакете MathCAD имеется ряд функций для решения уравнений:

• Find(x,y,…) – решение системы уравнений;

• Minerr(x,y,…) – приближенное решение системы уравнений;

• root(f(x),x,a,b) – решение одного уравнения с одним неизвестным;

• lsolve(M,V) – решение системы уравнений;

• polyroots(V) – приближенное решение одного уравнения с одним неизвестным, заданного полиномом.

Пример 30. Решить следующее линейное уравнение 4x-2=0.

1. Выведите на экран панель: Калькулятор.

2. Установите курсор на рабочей области и запишите уравнение в виде 4*X-2.

3. Подведите курсор к переменной x и выполните команду Символика>Переменная>Разрешить – на экране появится результат (рис. 43).

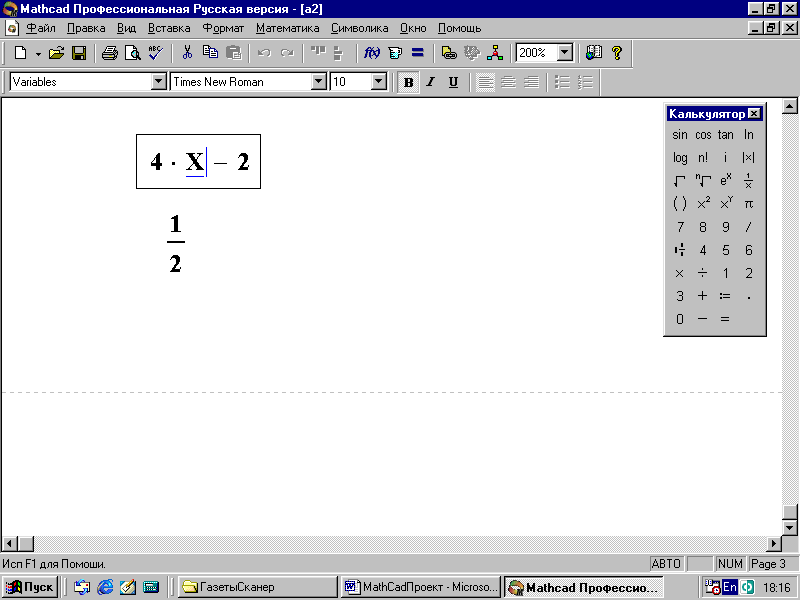
Рис. 43. Решение линейного уравнения