2.8. Векторы и матрицы
Пример 20. Выполнить операции над векторами: умножение вектора на число, сложение векторов, скалярное произведение векторов.
Для записи выражения выведите на экран панель Калькулятор, выполнив команду: Вид>Панели>Вычисления.
Для работы с векторами и матрицами выведите на экран панель Матрица, выполнив команду Вид>Панели>Матрица (рис. 36).
Установите курсор в то место рабочей области, куда следует вводить формулу, – на экране появится красный крестик.
Для записи вектора наберите V:=
Нажмите на панели Матрица кнопку
[Матрица или
Вектор];
В появившемся окне в поле Строк введите 2 и в поле Колонок введите 1 и нажмите кнопку [OK].
Заполните появившийся шаблон вектора произвольными значениями его элементов, например: 6 и 7.
8. Для умножения вектора на любое число, например, 5, запишите Y:=V*5 при использовании панели Калькулятор.
9. Для отображения результата умножения наберите Y= . После чего на экране появится Y = (30 35).
10. Найдите сумму векторов: V и Y, написав формулу Z:=V+Y с использованием панели Калькулятор.
11. Получите скалярное произведение векторов: V и Y, воспользовавшись кнопкой [Продукт точки*] на панели Матрица. Результат и алгоритм представлены на рис. 36.
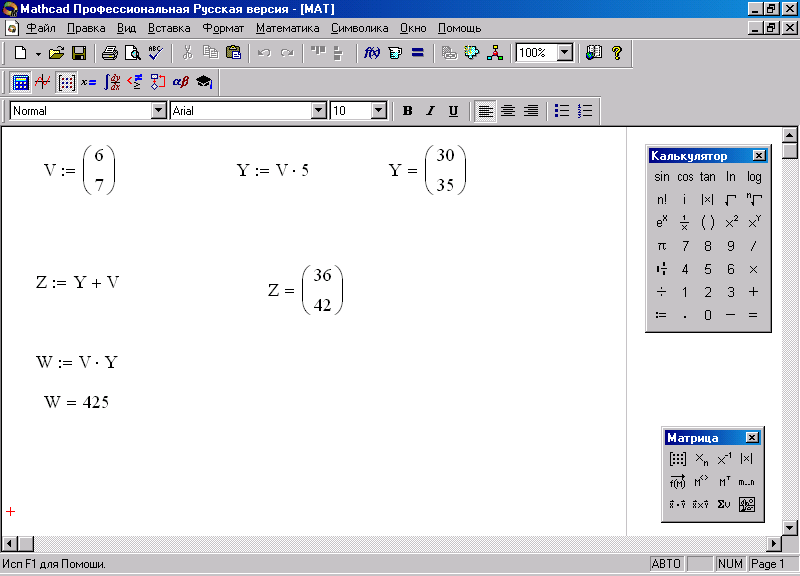
Рис. 36. Работа с векторами
Пример 21. Найти определитель матрицы A. Сложить и перемножить матрицы А и В. Найти обратные и транспонированные матрицы к данным матрицам А и В.
Для записи выражения выведите на экран панель Калькулятор, выполнив команду: Вид>Панели >Вычисления.
Для работы с матрицами выведите на экран панель Матрица, выполнив команду Вид>Панели >Матрица.
3. Установите курсор в то место рабочей области, куда следует вводить формулу (рис. 37).
4. Для записи матрицы А наберите А:= и нажмите кнопку [Матрица или Вектор] на панели Матрица.
5. В появившемся окне в поле Строк введите, например, 2, в поле Колонок введите тоже 2 и нажмите кнопку [OK].
6. Введите произвольные значения элементов матриц в появившиеся их шаблоны.
7. Для нахождения определителя матрицы
А воспользуйтесь
кнопкой
[Детерминант] на панели Матрица,
в появившейся шаблон введите А
и нажмите знак равенства =.
И произойдет вычисление определителя
матрицы А.
Найти определитель матрицы можно и другим способом: выделите матрицу и выполните команду Символика>Матрица>Детерминант. Результат получится аналогичный.
8. Проделайте те же операции и с матрицей B.
9. Для сложения двух матриц наберите А+В=, а для их произведения А*В=.
10. Транспонированные и обратные матрицы получаются при использовании панели Матрица и соответственно кнопок: [Инверсия] и [Перемещение матрицы].
На рис. 37 представлены алгоритм и результаты выполнения операций.
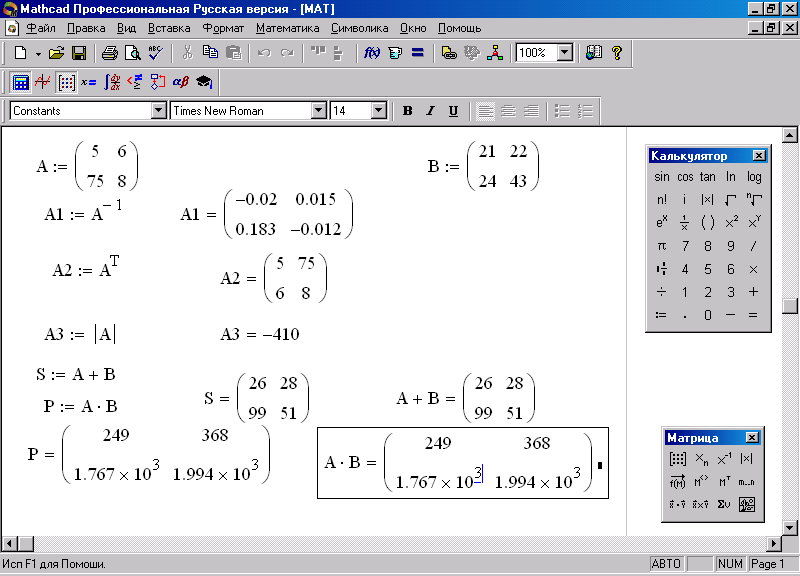
Рис. 37. Работа с матрицами
2.9. Векторы и матрицы в экономических задачах
Пример 22. В первом полугодии отчётного и текущего годов бюро рационализаторских предложений и изобретений приняло соответственно z1 и z2 предложений; во втором полугодии соответственно – c1 и c2 предложений. Сколько всего рационализаторских предложений было принято в отчетном и текущем годах.
Имеем два двухмерных вектора Z=(z1,z2) и С=(c1,c2). Решение задачи сводится к нахождению суммы этих векторов (рис. 38).
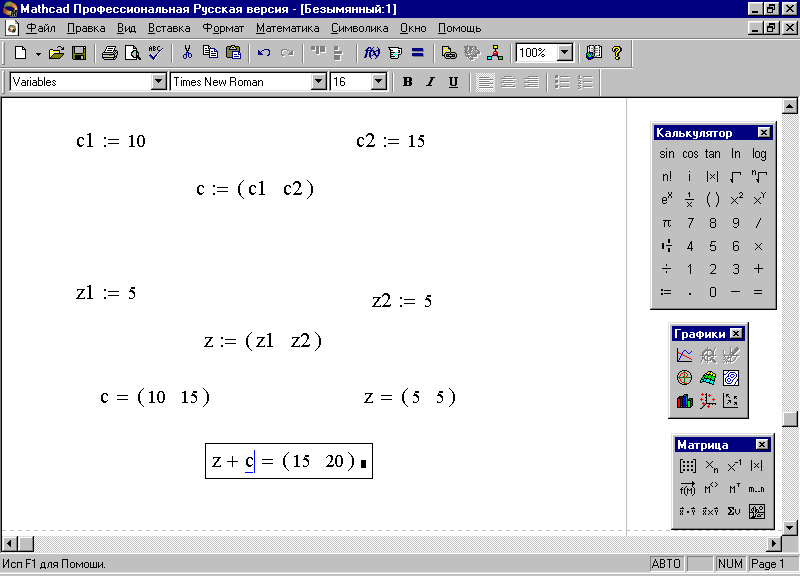
Рис.38. Определение количества рационализаторских предложений
Пример 23. На основании табеля учета использования рабочего времени и подсчета заработка учителям школы произведено начисление заработной платы за месяц. В этом же месяце у каждого учителя произведены удержания подоходного налога, аванса, профсоюзных взносов и другие удержания. Определить сумму к выдаче.
Исходные данные сведем в таблицу 4 и введем условные обозначения исходных данных:
Таблица 4. Ведомость начислений и удержаний
ФИО |
Начислено |
Удержано |
F |
H |
Y |
Задача сводится к нахождению разности двух векторов Н и Y, где элементами каждого вектора являются суммы начислений и удержаний для n работников.
Пример 24. Известны объёмы выпуска n продуктов предприятием в денежном выражении: Х1, Х2,…, Хn и объём соответствующих затрат: Y1,Y2,…,Yn, где n – номер продукта. Найти прибыль, т.е. разницу между затратами и выпуском по каждому продукту.