7. Графики в экономических задачах

Пример 17. При оплате за поездку в такси взимается некоторая сумма – b за посадку, а далее оплата зависит от стоимости одного километра поездки – k и покрытых километров – x. Требуется построить график, отражающий зависимость оплаты за поездку от километража.

Исходя из условия задачи ясно, что формула для расчета оплаты за поездку будет следующей: y=kx+b. То есть мы имеем уравнение прямой с угловым коэффициентом – k и свободным членом – b.

Следует построить график по алгоритму, аналогичному в примере 10, взяв произвольные значения коэффициента и свободного члена, например: 5 и 3.

1. Для записи функции выведите на экран панель Калькулятор, выполнив команду: Вид>Панели >Вычисления.

2. Для работы с графиками выведите на экран панель Графики, выполнив команду: Вид>Панели >Графики.

Установите курсор в то место рабочей области, куда следует вводить формулу.

2. Наберите требуемую функцию, у нас f(х):=5х+3 (не путать знак := со знаком =), используя клавиатуру и панель Калькулятор, и нажмите клавишу [Enter].

5. Для построения графика заданной функции:

• нажмите на панели Графики кнопку [График] – и в рабочем поле появится прямоугольник, представляющий собой декартовы координаты;

• напишите на оси абсцисс в маркере-шаблоне имя переменной х, а на оси ординат в таком же маркере – имя функции f(х).

Запомните (!), что в качестве имени функции следует набирать: f(x), y(x), – а не f, y.

• щелкните мышью на рабочей области – на экране появится график требуемой функции (рис. 33).

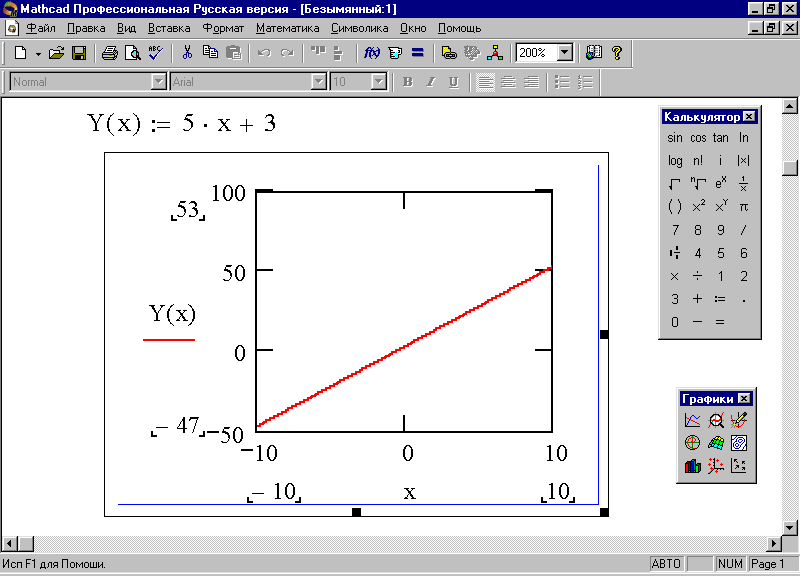
Рис. 33. Определение зависимости платы за проезд от километража

Пример 18. На склад, где имеется запас продукции на некоторую сумму – b, поступило два вида новой продукции в количестве: k1 и k2, по цене: x1 и x2 соответственно. Построить график зависимости стоимости продукции от цен.

Зависимость общей суммы за продукции от цен может быть представлена уравнением вида: y=k1*x1+k2*x2+b. Мы имеем уравнение поверхности, и алгоритм построения графика, например, при k1= 10, k2=20, b=15 будет таким:

1. Для записи функции выведите на экран панель Калькулятор, выполнив команду: Вид>Панели >Вычисления.

2. Для работы с графиками выведите на экран панель Графики, выполнив команду: Вид>Панели >Графики.

3. Установите курсор в то место рабочей области, куда следует вводить формулу.

4. Наберите на клавиатуре требуемую функцию, например, y(х1,x2):=10*х1+20*x2+15 (не путать знак := со знаком =), используя панель Калькулятор, и нажмите клавишу [Enter].

4. Для построения графика заданной функции:

• нажмите на панели Графики кнопку [Поверхностный График] – на экране появится область для построения поверхности, в которой лишь один маркер-шаблон;

• ведите в этот шаблон только имя функции, не указывая аргументы;

• щелкните мышью на рабочей области – на экране появится график требуемой функции (рис. 34).

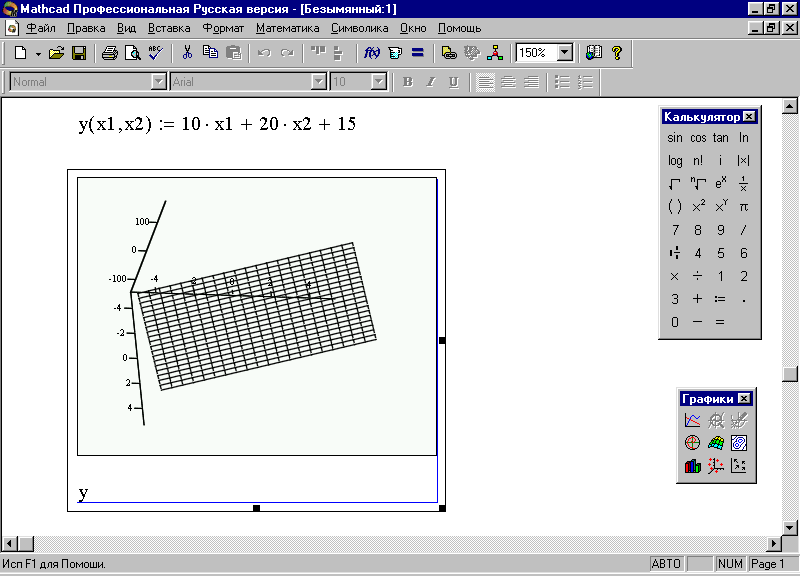
Рис. 34. График зависимости суммы от цен

Пример 19. В начале НЭП (Новая экономическая политика) в СССР функционировало несколько систем денежных единиц, – екатеринки, рубли, золотые десятки, американские доллары, злотые. В Национальный банк частные ростовщики сдавали деньги в различных денежных единицах.

Определить сданные в банк суммы в рублях, если известны: сданные суммы и соответствующие коэффициенты перевода одних денежных единиц в другие. Найти также общую сумму сданных денег.

Сведем данные задачи в таблицу 3, введя в ней условные обозначения:

Денежные единицы Таблица 3

№ n/n	ФИО ростовщика	Сданная сумма	Единицы измерения	Коэффициент перевода	Сумма, руб.
1	F1	C1	E1	K1	S1
2
3
…	…	…	…	…	…
n	Fn	Cn	En	Kn	Sn
Итого:

Будем считать, что в банк обратились два ростовщика. Тогда для них сданные ими суммы в рублях будут определяться по следующим формулам: С1*К1, С2*К2.

Общая сумма сданных денег будет вычисляться так: Y= С1*К1+С2*К2. Полученную формулу можно рассматривать как уравнение поверхности с переменными С1, С2 и коэффициентами К1, К2. Алгоритм построения этого графика при К1=10 И К2=15 аналогичен предыдущему примеру и представлен на рис. 35.

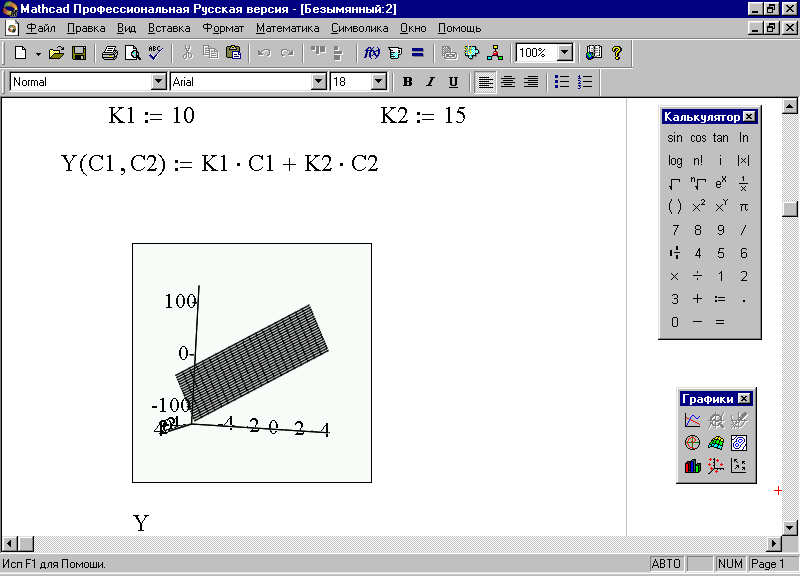
Рис. 35. График поступления денег в банк