6.6. Відбраковування грубих вимірів

Іноді при проведенні багаторазових вимірювань однієї величини виявляється, що одне або декілька значень істотно відрізняються від інших. Таки виміру, як правило, містять грубу помилку і називаються грубими або викидами. Перед побудовою довірливого інтервалу при заданій довірчій ймовірності β необхідно серію вимірювань перевірити на наявність викидів. Перевірка на викиди проводиться по U-критерію.

Критерій розраховується за формулою:

де - вимір, підозрювану на наявність грубої помилки.  Потім порівнюємо р з табличним значенням , яке визначається рівнем значущості р і кількістю ступенів свободи f = n-2. 

Якщо , то підозрювану значення не є грубою  помилкою. У разі, якщо , значення містить грубу  помилку, і, отже це вимір необхідно виключити з се ¬ рії. Після виключення всіх вимірювань, які містять грубі помилки, можна переходити до побудови довірчого інтервалу. Нижче приводиться числовий приклад розрахунку точкових оцінок, відбраковування грубих вимірів і побудова довірчого інтервалу. 

Приклад 6.6

Для вибірки об'ємом 4 провести отбраковку вимірювань, тобто визначити вимірювання, що містять грубу помилку і виключити їх з серії. Отримані наступні виміри: X = 4,13; х2 = 4,65; х3 = 4,62; х = 4,54. Рівень значущості  р = 0,05.

Послідовність рішення задачі буде наступною. 

А. Визначаємо вибіркове середнє: 

=4,485

У редакторі Excel розраховуємо це значення з використанням функції СРЗНАЧ, яка повертає середнє арифметичне кінцевого числа аргументів. 

Б. Розраховуємо вибіркову дисперсію випадкової величини: 

= 0,058

(з використанням статистичної функції ДІСП). 

В. Досліджуємо вибірку на наявність грубих помилок. 

Для цього розраховуємо значення критерію для вимірювань, підозрюваних на наявність грубої помилки.  Нехай підозрювану на наявність грубої помилки буде значення ​​= 4,13. Тоді розрахункове значення критерію буде

= = 1,7005

   Табличне значення критерію = 1689. 

Так як то, з імовірністю β = 0,95 підозрювану значення є грубою помилкою. Виключаємо його з серії. Обсяг серії зменшується на 1. Після виключення всіх вимірювань, які містять грубі помилки можна переходить до побудови довірчого інтервалу за методикою, викладеною в розділі 6.5.

Глава 7. Апроксимація експериментальних даних

  На практиці часто ставиться задача згладжування експериментальних даних, або задача апроксимації.

Постановка завдання. Нехай є дані, отримані практичної-ким шляхом (у ході експерименту або спостережень), які можна представити n парами чисел ( ; ). На основі цих даних потрібно підібрати таку функцію = φ ( , х), яка найкращим чином згладжувала б експериментальну залежність між змінними і по можливості точно відображала б загальну тенденцію залежності між і , де  - експериментальні значення змінних, - експеріментальний значення функції, - розрахункові значення емпіричною функції, - параметри функції.  Побудова емпіричної функції зводиться до обчислення входячих в неї параметрів , таких щоб з усіх функцій вибрати ту, яка краще за інших описує залежність між досліджуваними величинами. В якості критерію оцінки використовується квадратичний, в якому сума квадратів різниці між експериментальними значеннями і значеннями, обчисленими за апроксимуючої залежності, повинна бути мінімальна:

    Cr = ²→min

В Excel для побудови апроксимуючої функції попередньо будується графік експериментальної залежності, причому можна використовувати як конкретні значення , так і абстрактні значення (замість значень будуть номери точок), потім проводиться підбір апроксіміручої функції (лінії тренда) . Можливі наступні варіанти функцій.

1. Лінійна - (х) = ах +b. Зазвичай застосовується в найпростіших випадках, коли експериментальні дані зростають або убувають з постійною швидкістю.  2. Поліноміальна - (х) = + + + … + де =1, 2,...,6) - константи. Ступінь полінома визначається кількістю екстремумів.  3. Логарифмічна - (х) = а ln x + b. Застосовується для опису експериментальних даних, які спочатку швидко ростуть або спадають, а потім поступово стабілізуються. 

4. Степенева - (х) = b* . Дані не повинні мати нульових або негативних значень.

5. Експоненціальна - (х) = b* . Застосовується для опису експериментальних даних, які спочатку швидко ростуть або спадють, а потім поступово стабілізуються.

В Excel ступінь близькості апроксимації експериментальних даних обраної функцією оцінюється коефіцієнтом детермінації ( ). Якщо є декілька відповідних варіантів типів апроксимуючих функцій, то потрібно вибрати функцію з великим коефіцієнтом детермінації (прагнучим до 1).  На графіку експериментальних даних клацанням правої кнопки миші викликати випливали контекстне меню і вибрати пункт Додати лінію тренду. У діалоговому вікні Лінія тренда на вкладці Тип вибирається вид апроксимуючої функції, а на вкладці Параметри задаються додаткові параметри. 

Приклад 7.1

Підібрати апроксимуючу функцію, розташовуючи наступними даними: 

Рік	Виробництво продукції
1999	17,1
2000	18
2001	18,9
2002	19,7
2003	19,7
2004	19,9

Рис.7.1 Графік експериментальної залежності

Рішення:  1. Вводимо дані в таблицю Excel. 

2. По введених даних будуємо графік. Для цього викликаємо Майстер діаграм і вибираємо тип діаграми Графік. Задаємо параметри графіка (рис. 7.1).  3. Покажчик миші встановлюємо на одну з точок графіка і клацаємо правої кнопкою миші. У контекстному меню вибираємо Додати лінію тренду (рис. 7.2). 

Рис. 7.2. Контекстне меню

Рис. 7.3. Вибір виду апроксимуючої залежності 

4. З'являється діалогове вікно Лінія тренда. На вкладці Тип вибираємо тип лінії тренда - Поліноміальна і ступінь 2 (рис. 7.3). 

Потім на закладці Параметри встановити прапорці в поля показувати рівняння на діаграмі і помістити на діаграму величину достовірності апроксимації. Тоді описаний вище коефіцієнт детермінації (або величина достовірності апроксимації) і шукане рівняння ¬ ня апроксимуючої функції (х) з'являться на графіку. Після чого натискаємо кнопку ОК.  В результаті на діаграмі виходить апроксимує крива Поліноміальний (Виробництво продукції), при цьому точність апроксімації досить висока - = 0,9888 (рис. 7.4). 

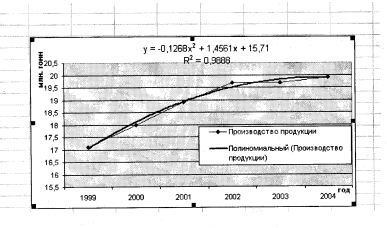
Рис. 7.4. Поліноміальна апроксимація 

Можна побудувати апроксимуючу функцію лінійну ( = 0894) (рис. 7.5), логарифмічну ( = 0,9716), поліноміальну ступеня 3 ( = 0,9899) і т.д., і вибрати з них найкращу. 

    Рис. 7.5. Лінійна апроксимація

Контрольні завдання