6.2. Визначення основних статистичних характеристик

  У майстрі функцій Excel ( - категорія СТАТИСТИЧНІ) має ряд спеціальних функцій, призначених для обчислення вибіркових характеристик.  • Функція СРЗНАЧ обчислює середнє арифметичне з нескількох масивів (аргументів) чисел.

• Функція СРГАРМ дозволяє отримати середнє гармонійне безлічі даних. Середнє гармонійне - це величина, зворотня до середнього арифметичного зворотніх величин.

• Функція СРГЕОМ обчислює середнє геометричне значень масиву позитивних чисел. Функцію можна використовувати для обчислення середніх показників динамічного ряду.

• Функція МЕДІАНА дозволяє отримати медіану заданої вибірки. Медіана - це такий елемент вибірки, для якого число елементів вибірки зі значеннями більше медіани дорівнює числу елементів вибірки зі значеннями менше медіани.  • Функція МОДА обчислює найбільш часто зустрічається значення у вибірці.  До спеціальних функцій, обчислювати вибіркові характеристики, відносяться ДІСП, СТАНДОТКЛОН, ПЕРСЕНТІЛЬ.

• Функція ДІСП дозволяє оцінити дисперсію за вибірковими даними.  • Функція СТАНДОТКЛОН обчислює стандартне відхилення. 

• Функція ПЕРСЕНТІЛЬ дозволяє отримати квантилі заданої вибірки.

  Приклад 6.1

  Дана вибірка з 10 експериментальних значень забрудненості повітря (концентрація чадного газу), отриманих протягом місяця.  У таблиці на рис. 6.1 для цієї вибірки розраховані статистичні характеристики з використанням майстра функцій.  

Рис. 6.1. Розрахунок точкових оцінок 

6.3. Вибіркова функція розподілу

  Завдання вибіркового методу полягає в тому, щоб зробити правильні висновки щодо всього зібрання об'єктів. Вибірковою (емпіричною) функцією розподілу випадкової величини X, побудованої за вибіркою , називається функція F (х), рівна частці значень , що задовольняє умовам 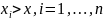. Для побудови виборочной функції розподілу весь діапазон зміни випадкової величини X розбивають на ряд інтервалів однакової ширини. Число інтервалів зазвичай вибирають не менше 5 і не більше 15. Потім визначають число значень випадкової величини X, що потрапили в кожний інтервал. Поділивши ці числа на загальна кількість спостережень n, знаходять відносну частоту попадання випадкової величини X в задані інтервали. За знайденими відносним частотах будують гістограму вибіркових функцій розподілу. Якщо відповідні точки відносних частот з'єднати ламаною лінією, то отримана діаграма буде називатися полігоном частот. При збільшенні розміру вибірки до безкінечності (на практиці, більше 30) вибіркові функції розподілу перетворюються на теоретичні. Гістограма перетворюється в графік щільності розподілу. А кумулятивна пряма, в якій по осі абсцис відкладаються інтервали, а по осі ординат - число або частки елементів сукупності, які мають значення менше або рівне заданому, - в графік функції розподілу.  В Excel для побудови вибіркових функцій розподілу використовуються спеціальна функція ЧАСТОТА і процедура пакета аналізу гістограми. 

Приклад 6.2

  Побудувати емпіричний розподіл ваги студентів в кілограмах для наступної вибірки:  64, 57, 63, 62, 58, 61, 63,60, 60,61, 65, 62, 62, 60,64,61, 59, 59,63,61,62, 58, 58, 63, 61, 59, 62,60,60, 58,61, 60,63, 63, 58,60, 59,60, 59, 61, 62, 62,63, 57,61, 58, 60, 64, 60, 59, 61,64, 62, 59, 65.

1. У діапазон А2: Е12 вводимо значення ваги студентів.  2. Виберемо ширину інтервалу 1 кг. Тоді при крайніх значеннях ваги 57 кг і 65 кг вийде 9 інтервалів. У діапазон G3: G11 введемо граничні значення інтервалів.  3. Заповнимо стовпець абсолютних частот. Для цього виділимо блок осередків НЗ: Н11. Викликаємо Майстер функцій на панелі інструментів ( ). У діалоговому вікні,що з’явилося

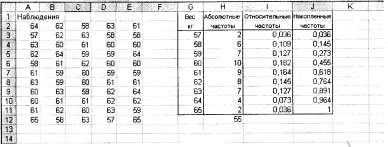
Рис. 6.2. Обробка результатів вибірки 

вибираємо категорію Статистичні та функцію ЧАСТОТА, натискаємо ОК. Покажчиком миші в робоче поле Масив даних вводимо діапазон даних спостережень А2: Е12. В робоче поле Двійковий масив - діапазон інтервалів G3: G11. Натискаємо комбінацію клавіш Ctrl + Shift + Enter. B стовпці Н3: Н11 з'явиться масив абсолютних частот.

4. В осередку Н12 знайдемо загальну кількість спостережень. Для цього встановимо курсор в осередок Н12. На панелі інструментів натискаємо кнопку Автосума ( ).Переконуємося, що діапазон підсумовування зазначений правильно (НЗ: Н11), натискаємо клавішу Enter. В осередку Н12 з'явиться число 55.

5. Заповнимо стовпець відносних частот. У комірку 13 вводимо формулу для обчислення відносної частоти: = H3 / H $ 13.Натискаємо клавішу Enter. Простягаємо введену формулу в діапазон 14:111. Отримуємо масив відносних частот.

6. Заповнимо стовпець накопичених частот. У комірку J3 копіюємо значення відносної частоти з комірки І3. У комірку J4 вводимо формулу: = J3 + I4. Натискаємо клавішу Enter. Простягаємо формулу в діапазон J5: J11. Отримуємо масив накопичених частот.

В результаті отримуємо таблицю, представлену на рис. 6.2.

Побудуємо діаграму відносних і накопичених частот. Для цього натиском миші викликаємо Майстер діаграм. У діалоговому вікні, вибираємо вкладку Нестандартні і тип діаграми Графік → Гістограма 2. Після натискання кнопки Далі вказуємо діапазон даних – І1: J11. Вводимо діапазон підписів по осі X. Для цього вибираємо вкладку Ряд, Підписи по осі X вказуємо діапазон G3: G11. Натискаємо кнопку Далі і вводимо назву осей X і Y: в робоче поле Вісь X (категорій)- Вага ; Вісь Y (значення) – відносн., частота; Друга вісь Y

Рис. 6.3. Діаграма відносних і накопичених частот

    Після редагування діаграма буде мати вигляд, як показано на малюнку  6.3. 

6.4. Перевірка відповідності експериментальних даних теоретичного розподілу  У більшості випадків при рішенні реальних задач закон розподілення емпіричних даних і його параметри невідомі. У той же час застосовуються в обробці даних статистичні методи в якості передумов часто вимагають певного закону розподілу. Найбільш часто перевіряється припущення про нормальний розподіл генеральної сукупності, так як більшість статистичних процедур орієнтоване на вибірки, отримані з нормально розподіленої генеральної сукупності. Для оцінки відповідності наявних експериментальних даних нормальному закону розподілу використовують графічний метод, вибіркові параметри форми розподілу та критерії згоди.

  Критеріями згоди називають статистичні критерії, призначені для перевірки згоди досвідчених даних і даних, розрахований ¬ них з теоретичної моделі. Тут нульова гіпотеза являє собою твердження про те, що розподіл генеральної сукупності, з якої отримана вибірка, не відрізняється від нормального. Серед  критеріїв згоди велике поширення отримав критерій хі-квадрат ( ). Він заснований на порівнянні емпіричних частот інтервалів угруповання з теоретичними (очікуваними) частотами, розрахований за формулами нормального розподілу. Для застосування критеріїв бажано, щоб обсяг вибірки (n) був більше 40 (n> 40), вибіркові дані були згруповані в інтервальний ряд з числом інтервалів не менше 7, а в кожному інтервалі знаходилося не менше 5 спостережень (частот) . 

В Excel критерій реалізований у функції ХІ2ТЕСТ. Функція ХІ2ТЕСТ обчислює ймовірність збігу спостережуваних (фактичних) значень і теоретичних (гіпотетичних) значень. Якщо обчислювана ймовірність нижче рівня значущості (0,05), то нульова гіпотеза відкидається і затверджується, що спостережувані значення не відповідають нормальному закону розподілу. Якщо обчислена імовірність близька до 1, то можна говорити про високий ступінь відповідності експериментальних даних нормальному закону розподілу.  Функція ХІ2ТЕСТ має наступні параметри:

ХІ2ТЕСТ (фактичніий_інтервал; очікуваємий_ інтервал),

де фактичний_інтервал - це інтервал даних, які містять спостереження, що підлягають порівнянні з очікуваними значеннями; очікуваний_ інтервал - це інтервал даних, який містить теоретичні (очікувані) значення для відповідних спостережень.

  Приклад 6.3

Для вибірки з прикладу 6.2 перевірити відповідність вибіркових даних нормальному закону розподілу. Для цього виконаємо два етапи обчислень ¬ ний.  Етап 1. Знайдемо теоретичні частоти нормального розподілу, попередньо визначивши середнє значення та стандартне відхилення вибірки.  В осередку 112 з допомогою функції СРЗНАЧ знаходимо середнє значення для діапазону А2: Е12 (рис. 6.4).

Аналогічно в комірці J12 за допомогою функції СТАНДОТКЛОН знаходимо стандартні відхилення для цих же даних. 

Потім за допомогою функції НОРМРАСП визначаємо теоретичні частоти. Встановлюємо курсор в комірку К3, викликаємо вказану функцію і заповнюємо

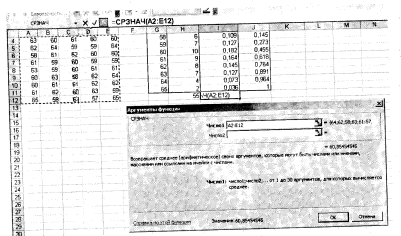
Рис.6.4 Застосування функції СРЗНАЧ

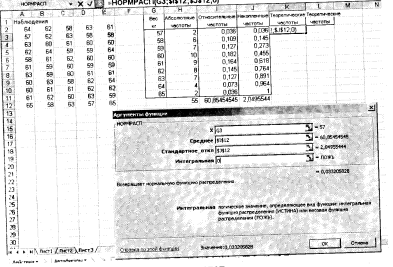
Рис.6.5. Розрахунок теоретичних частот

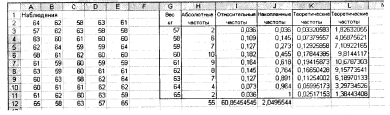
Рис. 6.6. Результати обчислень теоретичних частот 

її робочі поля: х - G3; Середнє - $I$12; Стандартне відхилення - $J$12; Інтегральний - 0 (рис. 6.5). Натискаємо ОК. Далі протягуємо ведену формулу в діапазон К3: К11. Потім заповнюємо стовпець L3:L11, ввівши формулу = Н$ 13*К4 в осередок L3 і розтягуючи її в діапазоні L3:L11. Результати обчислень показані на рис. 6.6. 

Етап 2. За допомогою функції ХІ2ТЕСТ визначимо відповідність даних нормального закону розподілу. 

Для цього встановлюємо курсор в вільну комірку L12. На панелі інструментів Стандартна натискаємо кнопку Вставка функції . У діалоговому вікні Майстер функцій вибираємо категорію Статистичні та функцію ХІ2ТЕСТ, потім ОК. Покажчиком миші в робочі поля вводимо фактичні НЗ: Н11 і очікувані L3:L11 діапазони частот. Потім - ОК. В осередку L12 появиться значення ймовірності того, що вибіркові дані відповідають нормального закону розподілу - 0,9842.

Результати обчислень показані на рис. 6.7.