МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ, МОЛОДЕЖИ И СПОРТА
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
Индивидуальное задание по предмету
«Информатика и информационные технологии»
на тему:
«Операции с матрицами. Статистическая
обработка экспериментальных данных»
Выполнила:
студентка группы 2-Г
химического факультета
Сигаева Анна Константиновна
2012 г.
5.5. Перемножування матриць
Добуток двох матриць визначено, якщо число стовпців першої матриці (множимо) дорівнює числу рядків другого матриці (множника).
Приклад 5.4
Нехай матриця А введена в діапазон А1: D3, а матриця В - в діапазон А5:С8. Необхідно знайти добуток цих матриць С = А х В.
Виділяємо блок осередків покажчиком миші при натиснутій лівій кнопці під результуючою матрицю. Якщо матриця А має розмірність 3х4, а матриця В має розмірність 4x3, то результуюча матриця С буде мати розмірність 3х3. Тому слід уважно стежити, щоб розмірність матриці С в точності відповідала визначенню добутка двох матриць. Нехай матриця С розміщуватиметься в діапазоні F1: НЗ.
Натискаємо на панелі інструментів Стандартна кнопку Вставка функції. У діалоговому вікні,що з’явилося, Майстер функцій в робочому полі Категорії вибираємо Математичні, а в робочому полі Функція - ім'я функції МУМНОЖ. Після цього натискаємо на кнопку ОК. Діалогове вікно, що з'явилося, МУМНОЖ мишею відсуваємо в сторону від початкової матриці і вводимо діапазон першої матриці А1: D3 в робоче поле Масив 1 (покажчиком миші при натиснутій лівій кнопці), а діапазон матриці В - А5: С8 - в робоче поле Масив 2 (рис. 5.8). Після чого, не натискаючи кнопку ОК, натискаємо поєднання клавіш CTRL+SHIFT+ENTER (рис. 5.9).
Якщо добуток матриць не з'явився в заданому діапазоні F1: Н3, то треба клацнути покажчиком миші в рядку формул і повторити натиснення клавіш CTRL+SHIFT+ENTER. У результаті в діапазоні F1: Н3 з'явиться зворотня матриця.
Рис. 5.8 Добуток двох матриць
Рис.5.9. Результат добутку двох матриць
5.6. Рішення систем лінійних алгебраїчних рівнянь з використанням матричних операцій
Багато
прикладних задач в техніці, економіці
та інших галузях зводяться до вирішення
системи лінійних рівнянь. Нехай
дана лінійна система n рівнянь з n
невідомими, де
(
i, j = 1,...,n) - відповідально коефіцієнти
при невідомих і вільні члени рівнянь:
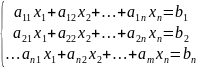
Дану систему можна записати у вигляді матричного рівняння:
=
,
де
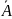- матриця коефіцієнтів;
- вектор невідомих;
– стовпчик вільних членів
Вектор невідомих X можна знайти, вирішуючи систему лінійних алгебраїчних рівнянь з використанням зворотної матриці, для чого, помножив ліву та праву
Рис. 5.10. Повертання матриці коефіцієнтів СЛАУ
частину
матричного рівняння на зворотну матрицю
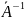зліва, отримаємо наступне розрахункове
співвідношення:
Для знаходження вектора невідомих необхідно:
ввести в діапазони клітинок матрицю і вектор ;
знайти за допомогою функції Excel МОБР зворотну матрицю ;
використовуючи функцію МУМНОЖ, знайти добуток на вектор . Результат буде шуканим вектором .
Приклад 5.5
Нехай матриця коефіцієнтів введена в діапазон А1: С3, а вектор-стовпчик правої частини - в діапазон Е1: Е3. Знаходимо зворотну матрицю коефіцієнтів з використанням функції МОБР (рис. 5.10). В результаті цієї операції елементи зворотної матриці А будуть розміщені в діапазоні А5:С7. Виділимо діапазон, в якому розміститься вектор невідомих - Е5:Е7. Викличемо функцію МУМНОЖ для множення матриці на вектор (рис. 5.11). Отриманий результат представлений на рис. 5.12.
Рис. 5.11 Множення зворотної матриці коефіцієнтів на вектор вільних членів
Рис. 5.12. Результати розв'язку СЛАУ