10. Закон сохранения полной механической энергии системы. Работа диссипативных сил.

Полная механическая энергия системы E=E_соб+U_внеш

E=K+U_соб+U_внеш

Закон сохранения полной механической энергии систем, находящейся во внешнем стационарном поле: если на систему частиц не действуют внешние сторонние силы и нет внутренних диссипативных сил, то полная механическая энергия системы остается постоянной:

E=E_соб+U_внеш=const – только в инерциальных системах отсчета

Работа диссипативных сил

Диссипативные силы – силы трения и сопротивления. Любая диссипативная сила может быть представлена в виде F=-k(u)v, v – скорость 1 тела относительно 2 тела, с которым оно взаимодейств.,

k(u) – положительный коэффициент, зависящий от скорости. F­¯v. Суммарная работа всех диссипативных сил в системе – всегда отрицательная величина, независимо от системы отсчета.

. Внутр. диссипат. силы в данной системе встречаются по парам(А₁= -А₂)

, F2=-F1, F1=-kv, v=v1-v2 – скорость 1 тела отн второго.

А_внутр=

Механика. Вопрос 18. Твердое тело. Разделение движения твердого тела на поступательное и вращательное. Преобразование поступательной и угловой скорости при переходе межу инерциальными системами отсчета.

Механика. Вопрос 19. Вращение твердого теле вокруг неподвижной оси. Момент инерции. Примеры вычисления момента инерции. Теорема Штейнера

Т еоре́ма Ште́йнера: момент инерции J тела относительно произвольной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями: J = Jc + m²d

Момент инерции, по определению:

Радиус-вектор можно расписать как сумму двух векторов:

где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

В ынося за сумму , получим:

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Т огда:

Откуда и следует искомая формула:

Примеры вычисления момента инерции

Механика. Вопрос 20. Кинетическая энергия вращающегося тела в системе центра инерции и в лабораторной системе.

Механика. Вопрос 21. Тензор инерции. Главные моменты инерции

Механика. Вопрос 22. Уравнения Эйлера

ЭЙЛЕРА УРАВНЕНИЯ в механике твердого тела. Динамические Э. у. представляют собой дифференц. ур-ния движения твёрдого тела вокруг неподвижной точки и имеют вид

где -моменты инерции тела относительно гл. осей инерции, проведённых из неподвижной точки; w_x, w_y, W₂-проекции мгновенной угл. скорости тела на эти оси; - гл. моменты сил, действующих на тело, относительно тех же осей; -производные по времени от Кинематические Э. у. дают выражения через Эйлера углы и имеют вид

Система ур-ний (1) и (2) позволяет, зная закон движения тела, определить момент действующих на него сил и наоборот, зная действующие на тело силы, определить закон его движения.

Механика. Вопрос 23. Неинерциальные системы отсчета. Силы инерции. Движение в поступательно движущейся НСО.

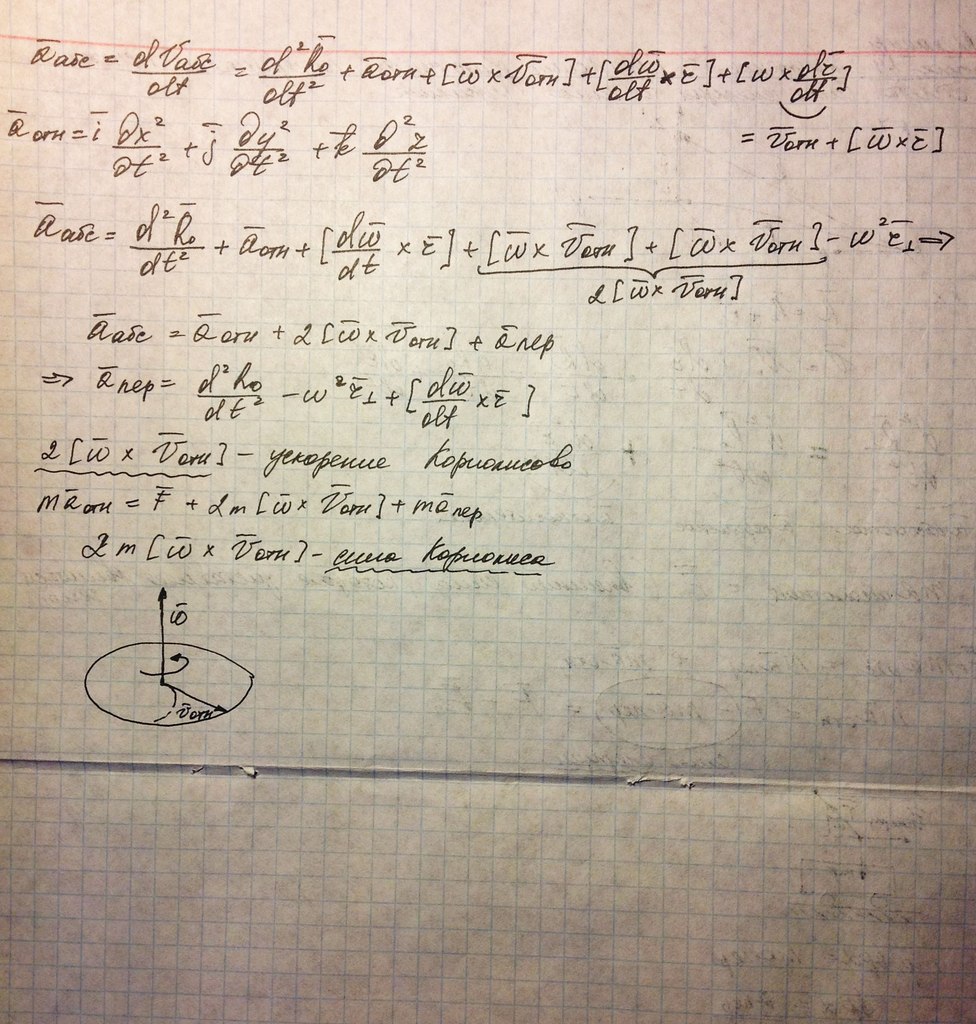
10. Распределение Больцмана. Распределение частиц в сосуде в однородном поле тяжести. Барометрическая формула.

Распределение Больцмана: В силу независимости событий (произведение вероятностей) для молекул иметь определенные значения кинетической и потенциальной энергий можно рассматривать отдельно распределение частиц во внешнем поле U(x,y,z)

dP(U)=B*exp(-U(x,y,z)/T)*dxdydz

Это соотношение дает вероятность того, что частица обладает потенциальной энергией U(x,y,z) и

находится в элементе объема dV= dxdydz вблизи точки с координатами (x,y,z). Так как вероятность

можно определить через отношение числа частиц, которые попадают в этот объем к полному числу частиц dP(U)=dP(x,y,z)=dN/N, то число молекул в объеме dV определяется формулой:

dN_x,y,z=N*B*e^-U(x,y,z)/Tdxdydz

Смысл множителя N*B легко понять, если рассмотреть число частиц в единице объема, т.е. плотность (концентрацию) числа частиц: dN_x,y,z/(dxdydz)=n(x,y,z)=N*B*e^-U(x,y,z)/T

видно, что произведение N*B равно плотности числа частиц, где потенциальная энергия

равна нулю U = 0, эту плотность обозначим n₀

n(x,y,z)=n₀*e^-U(x,y,z)/T – распределение Больцмана

Примечание: Если отсчет по энергии идет от точки, где U=U₀, тогда распределение Больцмана имеет вид:

n(x,y,z)=n₀*exp(-(U(x,y,z)-U₀)/T) (1)

Распределение частиц в сосуде по высоте в однородном поле тяжести.Будем считать,

что g=const, T= const. Для Земли однородное поле тяжести получаем для небольших высот h << Rз

(Rз - радиус Земли), когда раскладываем потенциальную энергию в ряд по степеням отношения h/R:

U(h)-U(0)=

M – масса Земли, а m - масса молекулы. Тогда подставляя в (1), получаем известную формулу

Больцмана, определяющую зависимость концентрации молекул от высоты:

n(h)=n(0)*exp(-mgh/T)=n(0)*exp(-mgh/kT_k)=n(0)*exp(-mgh/RT_k)

Здесь n(0) – концентрация молекул у дна сосуда (поверхности Земли), m-молярная масса газа

(m=mN_A), R - универсальная газовая постоянная. Концентрация частиц убывает с высотой,

причем концентрация более тяжелых частиц убывает с высотой быстрее. Это создает подъемную силу – силу Архимеда для более легких объектов (воздушные шары, аэростаты, дирижабли).

Воспользовавшись формулой для идеального газа: p=nkT

получаем барометрическую формулу Больцмана: p=p_0*exp(-mgh/kT_k)

Для более высоких температур распределение молекул по высоте сосуда становится более

равномерным. При этом полное число частиц в сосуде N постоянно и определяется

выражением:

здесь DS – площадь сечения сосуда, L – полная высота.

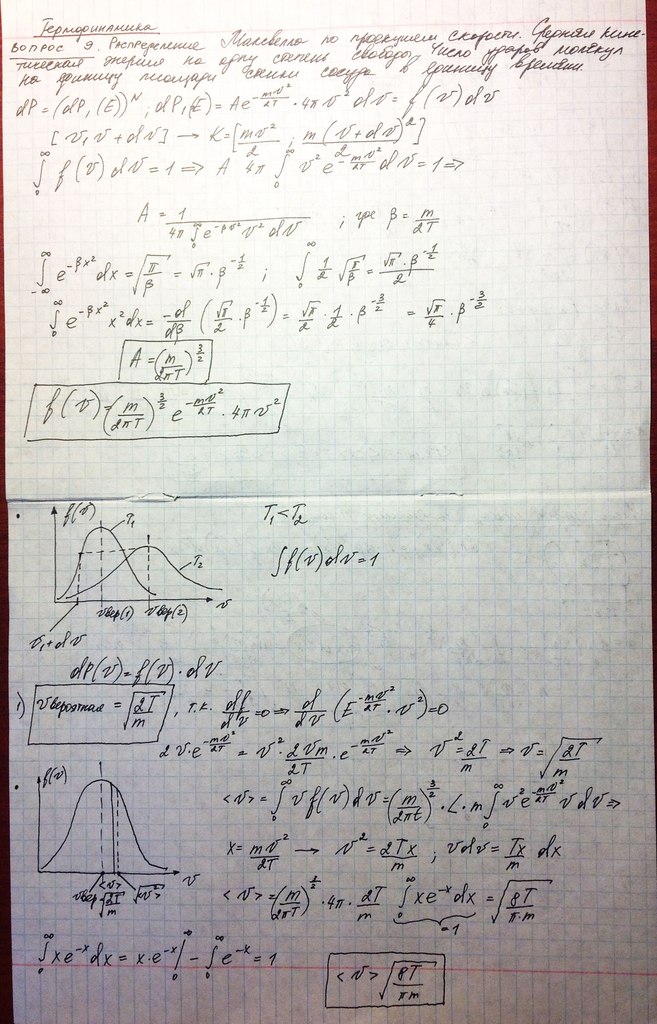
11. Распределение Максвелла-Больцмана. Средняя энергия на колебательную степень свободы.

Распределение Максвелла-Больцмана:

Для классической подсистемы полная энергия равна сумме

кинетической и E=K+U. И поскольку кинетическая энергия есть функция скоростей, а потенциальная энергия - функция координат, то вероятность иметь для подсистемы

полную энергию Е равна:

dP(E)=dP(K)dP(U)

Если в качестве подсистемы выбираем одну частицу, то для одной частицы имеем следующее распределение по энергиям:

dP(E)=Aexp dp_xdp_ydp_zdxdydz – распределение Максвелла-Больцмана

Средняя энергия, приходящаяся на колебательную степень свободы.

Распределение Максвелла-Больцмана позволяет получить среднюю энергию, приходящуюся на

колебательную степень свободы. Равновесное состояние кристалла - периодическое расположение атомов в пространстве. Однако, атомы не находятся в покое, они совершают малые тепловые колебания относительно положений равновесия. Пусть колебания совершаются вдоль оси 0x, тогда энергия такого осциллятора(то, что совершает колебания) равна: E=mv_x²/2+kx²/2, где m масса атома, k- упругая постоянная. Статистическое описание атомов с энергией Е можно вести с помощью распределения Максвелла-Больцмана, которое для одного одномерного осциллятора имеет вид:

Здесь А нормировочная постоянная, она состоит из произведения 2-х постоянных: А = А 1 А 2 , которые равны

соответственно:

Найдем среднюю энергию тела, колеблющегося по оси x, по стандартным формулам:

Очень сложными путями пришли к такому:

,T_k-температура в Кельвинах

Итак, на 1 колебательную степень свободы приходится энергия, равная Т = kT_k. Из расчета видно, что одна Т/2 возникла из-за усреднения кинетической энергии колебательного движения, а другая Т/2 - из-за потенциальной энергии колебательного движения.

12. Идеальный газ. Связь энергии и давления, закон Паскаля. Термодинамическое соотношение Гиббса. Условие механического равновесия(равенство давлений для подсистем замкнутой системы).

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Связь давления и энергии.

Рассмотрим замкнутую систему, состоящую из тела и среды, при этом объем этой системы постоянен

V=V₁+V₂=const. Пусть теплообмена между подсистемами нет, при этом энтропии подсистем S1 и S2

постоянны.

E₁=E(S₁,V₁)

Итак, если нет теплообмена, то энтропия постоянна S1 = const и всякое изменение объема V1

сопровождается изменением энергии Е1 .

Чтобы описать механическое взаимодействие объема V 1 с окружающей средой, построим на границе площадку размером dydz, перпендикулярную оси x. Пусть изнутри объема V1 на эту площадку действует сила F_x . Под действием этой силы тело (газ) совершает работу при перемещении этой площадки на расстояние dx:

dA_газ=F_xdx

Работа приводит к уменьшению внутренней энергии тела на

величину:

-dE=F_xdx, F_x=-dE/dx

Учитывая, что элемент объема равен dV=dxdydz:

А налогично для F_y, F_z:

(1)

1. - закон Паскаля: средняя сила, действующая на элементарную площадку в жидкости (газе, твердого тела), пропорциональна ее площади и направлена по нормали к ней.

Термодинамическое тождество.

Полное изменение внутренней энергии E=E(S,V) - есть полный дифференциал:

- термодинамическое тождество или термодинамическое соотношение Гиббса

Условие механического равновесия.

Тела 1 и 2 составляют замкнутую систему, следовательно, в состоянии равновесия можно записать:

E=E1+E2=const; V=V1+V2=const; S=S1(V1,E1)+S2(V2,E2)

Т.к. и то p₁/T₁=p₂/T₂

Если тела в тепловом равновесии, то p1=p2

При увеличении давления энтропия растет, при уменьшении давления возрастанию энтропии соответствует сжатие тела.

13. Квазистатические процессы(изотермический, изобарический, изохорический, политропический) и работа, совершаемая идеальным газом.

Элементарная работа газа dA=pdV, а конечная работа при расширении газа от V1 до V2:

pV=NT=NkT_k , для одного моля: Nk=N_Ak=R – газовая постоянная. Тогда pV=nRT_k (для n молей) – уравнение Менделеева-Клапейрона

Изотермический процесс: процесс, при котором температура остается неизменной T=const.

Работа n молей газа по расширению от объема V 1 до объема V 2 определяется уравнением:

Работа газа равна площади под кривой изотермы на графике P(V) от точки 1 до точки 2.

Изобарический процесс: процесс, при котором давление в газе остается неизменным p=const.

Работа n молей газа по расширению от объема V 1 до объема V 2 определяется очевидным соотношением (как площадь под графиком между объемами):

A₁₂=p(V2-V1)

Изохорический процесс: процесс, при котором объем газа остается неизменным V=const. Поскольку

изменение объема равно нулю dV= 0 , то и работа газа в этом процессе равна 0: A=0.

Политропический процесс определяется уравнением pVⁿ=const.

Пусть эта постоянная равна B. Тогда работа:

В зависимости от величины показателя политропы n работа газа при расширении может быть положительной и отрицательной.

14. Работа и количество тепла. Первое начало термодинамики.

Если тело испытывает теплообмен и механическое взаимодействие с окружающей средой, то изменение внутренней энергии определяется двумя причинами:

1)Работой внешних сил dA’

2) теплообменом, т.е. обменом той частью энергии, которая называется количеством теплоты dQ.

П олучаем: dE=dQ+dA’ => dQ=TdS

dE=TdS-pdV

Количество тепла зависит от способа перехода тела из одного состояния в другое. Так, совершая круговой процесс, получаем, что изменение внутренней энергии равно DE = 0, поскольку внутренняя энергия есть функция состояния. Однако, вследствие соотношения dE=dQ+dA’ можно получить работу и количество тепла, отличное от нуля. Т.е. возможно превращение работы в тепло и тепла в

работу при совершении кругового процесса.

Единицы теплоты: система СГС – Эрг, система СИ – Дж. Существует внесистемная

единица теплоты - калория (количество тепла при нагревании 1г воды на 1К): 1кал = 4.184 Дж

Таким образом, в равенстве

dE=dQ+dA’ выражается закон сохранения энергии, который носит название первого начала термодинамики. Для системы невзаимодействующей с окружающей средой имеем: dQ = 0, dA’= 0 и dE = 0, т.е. E = const.

Следует, что если теплоизолированное тело (dQ = 0) участвует в круговом процессе (dE = 0), то в этом процессе и dA = 0. Иначе: в отсутствие взаимодействия с окружающими телами нельзя провести процесс, единственным результатом которого было бы получение работы. Невозможно построить вечный двигатель первого рода.

Первое начало термодинамики можно записать: dQ=TdS=dE+pdV.

22. Реальные газы. Уравнение Ван-дер-Ваальса.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

При низких давлениях сжать реальный газ легче, чем идеальный, а при высоких давлениях - реальный газ сжимается труднее идеального. Т.е. опыт показывает, что между молекулами газа существуют силы притяжения и отталкивания. Их необходимо учитывать, чтобы описать поведение газа в более широком интервале. Так, идеальный газ не превращается в жидкость или в твердое тело, а реальные газы испытывают такие превращения, и причина тому - взаимодействие между молекулами.

В основе межмолекулярного взаимодействия лежат силы электромагнитной природы, эти силы на малых расстояниях имеют характер отталкивания, а на больших – характер притяжения. Впервые взаимодействие между атомами и молекулами рассматривал и учитывал при определении уравнения состояния реального газа И. Ван-дер-Ваальс.

Уравнение Ван-дер-Ваальса.

Уравнение Ван-дер-Ваальса для описания состояния реального газа является наиболее простым и удобным обобщением уравнения состояния идеального газа. Оно было получено опытным путем и отличается от уравнения состояния идеального газа поправками к давлению и объему газа. Эти поправки происходят от учета в рамках простейших модельных представлениях отталкивания молекул на малых расстояниях и притяжения на больших.

1). Учтем отталкивание на малых расстояниях.

Если заменить объем в уравнении состояния идеального газа на (V-b), то получиться:

т.е. при увеличении давления р газ можно сжать лишь до минимального объема, равного b (дальше возникает сильнейшее отталкивание).

2). Если учесть притяжение между молекулами. Поправку к давлению можно записать в виде:

где a - некоторая постоянная величина.

Окончательно уравнение Ван-дер-Ваальса для одного моля записывается в виде:

23.Изотермы Ван-дер-Ваальса. Отношение масс газообразной и жидкой фаз на двухфазном участке изотермы Ван-дер-Ваальса.

Изотермы Ван-дер-Ваальса.

Преобразуем уравнение Ван-дер-Ваальса для одного моля и запишем его по степеням объема, считая постоянной температуру:

При температурах, ниже некоторого значения Ткр, в уравнении имеется 3 вещественных корня. При этом изотерма имеет дополнительные максимум и минимум

в отличие от изотерм идеального газа. При Т < Ткр эта колоколообразная область немонотонной зависимости изображена на рис. 2.1 пунктирной линией, она сужается с ростом температуры Т и при Т = Ткр исчезает, а изотермы превращаются в кривые, близкие к изотермам идеального газа.

Итак, при Т = Ткр имеется точка перегиба, где все три решения для V сливаются в одно и мы

п олучаем одинаковые корни уравнения (4.2.1). Эта температура Ткр называется критической температурой. Соответствующая этой температуре изотерма также называется критической.

Отношение масс газообразной и жидкой фаз на двухфазном участке изотермы Ван-дер-Ваальса.

Изотерма имеет плоский участок, на котором осуществляется превращение одной фазы в другую. То есть с сокращением объема газ переходит в жидкость при постоянном давлении. Причем газ и

жидкость все время находятся в равновесии, т.е. при данном объеме мы имеем постоянное количество насыщенного пара над постоянным количеством жидкости. С молекулярной точки зрения – это динамическое равновесие: молекулы непрерывно переходят из одной фазы в другую. В крайней левой точке плоского участка мы получаем, что весь газ перешел в жидкость, т.е. получаем объем жидкости (Vж). Напротив, в правой точке этого участка мы получаем только объем газа (Vг, см рис. 2.3).

Получим отношение масс жидкости и пара при произвольном объеме на двухфазном участке.

или