
- •1. Вектор-функция скалярного аргумента Вектор-функция скалярного аргумента, годограф вектор функции
- •Предел, непрерывность, производная вектор-функции
- •Касательная. Нормаль к плоской кривой
- •Кривизна, радиус кривизны, кручение кривой
- •Соприкасающаяся плоскость. Естественный трехгранник Френе
- •Практикум Вектор-функция
1. Вектор-функция скалярного аргумента Вектор-функция скалярного аргумента, годограф вектор функции
Определение.
Если каждому значению параметра
![]() из некоторого промежутка отвечает
определенный вектор
из некоторого промежутка отвечает
определенный вектор
![]() (зависящий от
),
то вектор
называется векторной функцией (кратко
вектор-функция) от скалярного аргумента
и в этом случае пишут:
(зависящий от
),
то вектор
называется векторной функцией (кратко
вектор-функция) от скалярного аргумента
и в этом случае пишут:
![]() . (1.1)
. (1.1)
При изменении
аргумента
вектор
![]() изменяется как по величине, так и по
направлению. В дальнейшем будем
предполагать, что
изменяется в промежутке, конечном или
бесконечном.
изменяется как по величине, так и по
направлению. В дальнейшем будем
предполагать, что
изменяется в промежутке, конечном или
бесконечном.
Будем считать, что
вектор
исходит из начала координат, т.е.
− радиус-вектор некоторой точки
![]() .
В этом случае при изменении параметра
конец вектора
опишет линию
.
В этом случае при изменении параметра
конец вектора
опишет линию
![]() ,
называемую годографом векторной функции
.
При этом начало координат называют
полюсом годографа. Уравнение (1.1) называют
векторным уравнением кривой
(рис. 1.1).
,
называемую годографом векторной функции
.
При этом начало координат называют
полюсом годографа. Уравнение (1.1) называют
векторным уравнением кривой
(рис. 1.1).
Если у вектора меняется только модуль, то годографом его будет луч, исходящий из полюса. Если модуль вектора постоянен и меняется только его направление, то годограф есть линия, лежащая на сфере с центром в полюсе и радиусом, равным модулю вектора .

Рис. 1.1
Если через
![]() обозначить проекции вектора
на оси прямоугольной декартовой системы
координат в пространстве, то эти величины
для каждого значения параметра
в свою очередь принимают определенные
числовые значения и поэтому являются
скалярными функциями скалярного
аргумента
:
обозначить проекции вектора
на оси прямоугольной декартовой системы
координат в пространстве, то эти величины
для каждого значения параметра
в свою очередь принимают определенные
числовые значения и поэтому являются
скалярными функциями скалярного
аргумента
:
![]() ,
,
![]() ,
,
![]() . (1.2)
. (1.2)
И тогда
![]() . (1.3)
. (1.3)
Таким образом, задание векторной функции скалярного аргумента равносильно заданию трех скалярных функций того же аргумента. Т.к. уравнение (1.1) является уравнением некоторой кривой в пространстве, то ту же кривую задают уравнения (1.2). Уравнения (1.2) − обычные параметрические уравнения кривой в пространстве.
Пример. Рассмотрим кривую, заданную параметрически с помощью уравнений
![]() ,
,
![]() ,
,
![]() .
.
Эта кривая называется винтовой линией. Ее векторное уравнение
![]() .
.
При любом значении
параметра
![]()
![]() .
Это означает, что винтовая линия
расположена на цилиндре
.
Это означает, что винтовая линия
расположена на цилиндре
![]() .
Отсюда следует, что, когда точка
.
Отсюда следует, что, когда точка
![]() движется по винтовой линии, ее проекция
движется по винтовой линии, ее проекция
![]() на плоскости
на плоскости
![]() перемещается по окружности радиуса
перемещается по окружности радиуса
![]() и с центром в начале координат, причем
является полярным углом точки
.
Когда точка
описывает полную окружность, аппликата
и с центром в начале координат, причем
является полярным углом точки
.
Когда точка
описывает полную окружность, аппликата
![]() точки
винтовой линии увеличивается на
точки
винтовой линии увеличивается на
![]() .
Эта величина называется шагом винтовой
линии.
.
Эта величина называется шагом винтовой
линии.
Предел, непрерывность, производная вектор-функции
Пусть вектор-функция
определена в окрестности точки
![]() ,
кроме самой точки
,
кроме самой точки
![]() .
.
Вектор
![]() называется пределом векторной функции
при
называется пределом векторной функции
при
![]() (или в точке
),
если
(или в точке
),
если
![]() . (1.4)
. (1.4)
Если есть предел функции при , то это записывается так
![]() . (1.5)
. (1.5)
Если записать векторную функцию и вектор в проекциях
,
![]() ,
,
то получим
![]() . (1.6)
. (1.6)
Тогда из равенства (1.4) следует, что
![]() ,
,
![]() ,
,
![]() . (1.7)
. (1.7)
Свойства вектор-функции:
1. Если
,
то
![]() .
.
2.
![]() .
.
3.
![]() ,
,
![]() − скалярная функция.
− скалярная функция.
4.
![]()
5.
![]() .
.
Вектор-функция , определенная в некоторой окрестности точки , называется непрерывной в точке , если .
Из равносильности
(1.4) и (1.7) следует, что для того чтобы
вектор-функция
была непрерывной в точке
,
необходимо и достаточно, чтобы в этой
точке были непрерывны функции
![]() .
.
Введем понятие производной векторной функции
. (1.8)
Предполагаем, что начало вектора находится в начале системе координат (рис.1.2).

Рис. 1.2
Возьмем фиксированное
значение параметра, соответствующее
какой-либо точке определенной точке
на кривой, заданной уравнением (1.8), и
дадим параметру
приращение
![]() .
Тогда получим вектор:
.
Тогда получим вектор:
![]() ,
,
который определяет
некоторую точку
![]() .
Найдем приращение вектора:
.
Найдем приращение вектора:
 (1.9)
(1.9)
На рисунке, где
![]() ,
,
![]() .
Вектор приращения определяется вектором
.
Вектор приращения определяется вектором
![]() .
.
Рассмотрим
отношение приращения вектор-функции к приращению
скалярного аргумента; это есть вектор
коллинеарный с вектором
приращения вектор-функции к приращению
скалярного аргумента; это есть вектор
коллинеарный с вектором
![]() .
При этом вектор
в сторону, соответствующую возрастанию
параметра
.
.
При этом вектор
в сторону, соответствующую возрастанию
параметра
.
Далее с учетом (1.9) вектор можно представить в виде
![]() .(1.10)
.(1.10)
Если функции
имеют производные при выбранном значении
параметра
,
то множители при
![]() в равенстве (1.10) в пределе при
в равенстве (1.10) в пределе при
![]() обратятся в производные
обратятся в производные
![]() .
.
Значит,
![]() .
.
Вектор, определяемый
последним равенством, называется
производной от вектора
по скалярному аргументу
.
Ее обозначают
![]() или
или
![]() .
Итак,
.
Итак,
![]() . (1.11)
. (1.11)
Выясним направление
вектора
.
Заметим, что при
точка
стремится к точке
и поэтому секущая
![]() стремится к касательной в точке
.
Отсюда, производная
стремится к касательной в точке
.
Отсюда, производная
![]() является вектором, касательным к
годографу вектор-функции
является вектором, касательным к
годографу вектор-функции
![]() ,
направленным в сторону, соответствующую
возрастанию параметра
.
,
направленным в сторону, соответствующую
возрастанию параметра
.
Из (1.11) следует, что
![]() . (1.12)
. (1.12)
Дифференциал длины дуги кривой равен
![]() ,
,
откуда
![]() . (1.13)
. (1.13)
Из (1.12) и (1.13) имеем
![]() . (1.14)
. (1.14)
Таким образом,
модуль производной вектор-функции
![]() равен производной от длины годографа
по аргументу
.
равен производной от длины годографа
по аргументу
.
Правила дифференцирования вектор-функции:
Если
 -
постоянный
вектор,
то
-
постоянный
вектор,
то
 .
.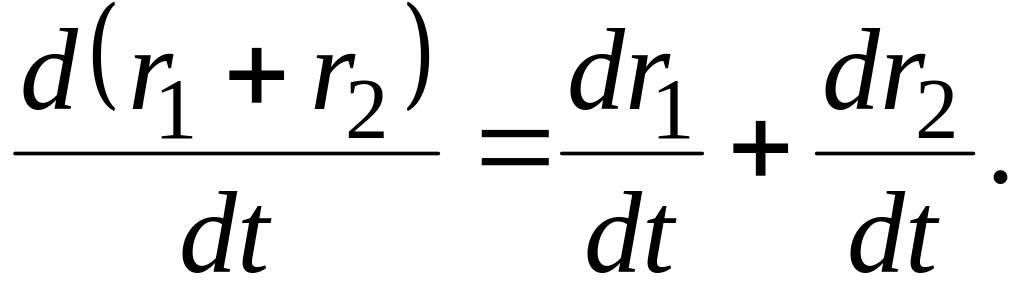
 ,
где
,
где
 -скалярная
функция.
-скалярная
функция. ,
,
 скалярное
произведение.
скалярное
произведение. ,
,
 векторное
произведение.
векторное
произведение.
Последовательным дифференцированием можно найти производные высших порядков
![]() и т.д.
и т.д.
