1. Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конеч­ном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энер­гии и т. д.). Например, температура тела определяется скоростью хаотического движе­ния его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в слу­чае большого числа молекул.

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехо­да между этими состояниями. Термодинамика не рассматривает микропроцессы, кото­рые лежат в основе этих превращений. Этимтермодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных за­конах, установленных в результате обобщения опытных данных.

2. Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средойэнергией и веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.

ТЕРМОДИНАМИЧЕСКОЕ СОСТОЯНИЕ - равновесное макроскопич. состояние термодинамической системы, к-рое фиксируется заданием параметров состояния, представляющих собой измеряемые макроскопич. приборами ср. величины определ. набора характеристик системы.

Стационарное состояние в физике, состояние физической системы, при котором некоторые существенные для характеристики системы величины (различные в разных случаях) не меняются со временем.

РАВНОВЕСНОЕ СОСТОЯНИЕ - состояние, в к-рое приходит термодинамич. система при постоянных внеш. условиях. Р. с. характеризуется постоянством во времени термодинамич. параметров и отсутствием в системе потоков вещества и энергии

3. Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние), физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Т. одинакова для всех частей изолированной системы, находящейся вравновесии термодинамическом. Если изолированная система не находится в равновесии, то с течением времени переход энергии (теплопередача) от более нагретых частей системы к менее нагретым приводит к выравниванию Т. во всей системе (первый постулат, или нулевое начало термодинамики).Т. определяет: распределение образующих систему частиц по уровням энергии (см. Больцмана статистика) и распределение частиц по скоростям (см. Максвелла распределение); степень ионизации вещества (см. Саха формула); свойства равновесного электромагнитного излучения тел — спектральную плотность излучения (см. Планка закон излучения), полную объёмную плотность излучения (см. Стефана — Больцмана закон излучения) и т. д. Т., входящую в качестве параметра в распределение Больцмана, часто называют Т. возбуждения, в распределение Максвелла — кинетической Т., в формулу Саха — ионизационной Т., в закон Стефана — Больцмана — радиационной температурой. Поскольку для системы, находящейся в термодинамическом равновесии, все эти параметры равны друг другу, их называют просто температурой системы. В кинетической теории газов и др. разделах статистической механики Т. количественно определяется так, что средняя кинетическая энергия поступательного движения частицы (обладающей тремя степенями свободы) равнакТ, где k — Больцмана постоянная, Т — температура тела. В общем случае Т. определяется как производная от энергии тела в целом по его энтропии. Такая Т. всегда положительна (поскольку кинетическая энергия положительна), её называют абсолютной Т. или Т. по термодинамической температурной шкале. За единицу абсолютной Т. в Международной системе единиц (СИ) принят кельвин(К). Часто Т. измеряют по шкале Цельсия (t), значения t связаны с Т равенством t = Т √ 273,15 К (градус Цельсия равен Кельвину). Методы измерения Т. рассмотрены в статьях Термометрия, Термометр.

4. Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное

Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется.

ИЗОБАРНЫЙ ПРОЦЕСС ( )

ИЗОХОРНЫЙ ПРОЦЕСС ( )

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС ( )

5. Закон Бо́йля — Марио́тта — один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в1676 году. Описывает поведение газа в изотермическом процессе. Закон является следствием уравнения Клапейрона^[1].

Закон Бойля — Мариотта гласит:

При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно.

В математической форме это утверждение записывается следующим образом

где   — давление газа;   — объём газа.

Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молярная масса газа, тем больше это отличие.

6. Закон Гей Люссака — при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре

  

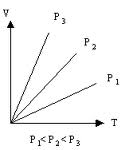
Объем V данной массы газа при постоянном давлении газа прямо пропорционален изменению температуры

  

Закон Гей-Люссака справедлив только для идеальных газов, реальные газы подчиняются ему при температурах и давлениях, далеких от критических значений. Является частным случаем уравнения Клайперона.

7. Французский ученый Ж. Шарль в 1787 году нашел экспериментально зависимость давления газа от температуры при постоянном объеме. Данные лежат в основе газового закона Шарля.

      Формулировка закона Шарля следующая: для данной массы газа отношение давления газа к его температуре постоянно, если объем газа не меняется. Эту зависимость математически записывают так:

P/Т=const, если V=const и m=const

8. АВОГА́ДРО ЗАКО́Н, один из основных законов идеальных газов: в равных объемах идеальных газов при одинаковых давлении и температуре содержится одинаковое число молекул. Число молекул в одном моле называют постоянной Авогадро или числом Авогадро. Закон был открыт А. Авогадро в 1811.

Согласно закону Авогадро, 1 моль любого идеального газа при нормальных условиях занимает одинаковый объем. При давлении р =101,325 кПа и температуре Т = 273,15 К этот объем равен 22,41383 м³. Следовательно, моль любого вещества содержит одно и то же число молекул, равное числу Авогадро 6,022045(31)^.10²³ моль^-1.

Из закона Авогадро следует, что при одних и тех же давлении и температуре плотности двух идеальных газов прямо пропорциональны, а удельные объемы обратно пропорциональны их молекулярным массам.

9. Воздух в комнате, где мы находимся, представляет собой смесь нескольких газов, в основном — азота (около 80%) и кислорода (около 20%). Парциальное давление каждого из этих газов — это давление, которое имел бы газ, если бы он один занимал весь объем. К примеру, если бы все газы, кроме азота, удалили из комнаты, то давление того, что осталось, и было бы парциальным давлением азота. Закон Дальтона утверждает, что общее давление всех газов вместе взятых равно сумме парциальных давлений каждого газа в отдельнсти. (Строго говоря, закон применим только кидеальным газам, но с достаточно хорошим приближением он описывает также и реальные газы.)

Джон Дальтон сформулировал этот закон в 1801 году, хотя молекулярно-кинетическая теория газов (модель, описывающая поведение газов), из которой он непосредственно вытекает, была разработана позже — уже в середине XIX века. Давление газа на стенки сосуда представляет собой результат столкновения молекул газа с этими стенками. Рассматривая газ с этих позиций, нетрудно понять, что количество столкновений со стенкой молекул каждого вида будет зависеть от того, как много молекул этого вида присутствует в газе. А из этого следует, что общее давление, представляющее собой сумму столкновений всех молекул, получается при сложении числа столкновений молекул каждого вида.

10.

Уравнение Менделеева Клапейрона — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа

Из Уравнения Менделеева-Клапейрона выводятся 3 закона :

1) Закон Шарля :    

2) Закон Гей-Люссака :    

3) Закон Боля-Мариотта :    

11. Основное уравнение МКТ связывает микропараметры частиц ( массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р - давление, V - объем, Т - температура).  Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы. Ниже приведены различные выражения для основного уравнения МКТ:    где р - давление газа на стенки сосуда(Па) n - концентрация молекул, т.е. число молекул в единице объема ( 1/м3)    - масса молекулы (кг)   - средний квадрат скорости молекул ( м2/с2) ρ - плотность газа (кг/м3)  - средняя кинетическая энергия молекул (Дж) Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.

12.

13. температура-мера средней кинетической энергии молекул

14. Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений

Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.