31. Расчетные методы квантовой химии. Общая характеристика.

Все расчёты многоатомных молекул основаны на приближенных решениях уравнения Шредингера. Существуют 2 главных требования к уровню приближения и выбору расчётной схемы: 1. достаточное соответствие результатов расчёта результатам эксперимента; 2. достаточная экономичность расчётов, т.е. разумные затраты времени при выполнении их на быстродействующих компьютерах. Из двух основных теорий химической связи – метода валентных связей иметода молекулярных орбиталей, последний имеет значительные преимущества при реализации на РС. Поэтому все основные расчётные методы современной квантовой химии используют приближение МО (молекулярных орбиталей) в форме схемы ЛКАОМО-Хартри-Фока-Рутаана. В рамках этой схемы возможны усовершенствования расчётной модели – учёт эффектов электронной корреляции.

Первостепенной задачей теоретического изучения межмолекулярных взаимодействий и их влияния на физико-химические свойства молекулярных систем является расчёт оптимизированной геометрической структуры наноразмерного кластера, которая представляет собой важную квантово-химическая проблему. Благодаря развитию вычислительной техники большую популярность приобрели методы квантово-химического (полуэмпирического и неэмпирического) моделирования. Они не имеют жёсткой привязки к узким классам органических соединений, и способы учесть множество эффектов (в частности, стереохимических и конформационных), которые не могут быть рассмотрены в явном виде под структурными эмпирическими методами расчёта.

32. Первопринципные методы расчета.

Наиболее удобным с точки зрения квантовой химии является такой метод расчёта структуры и свойств молекулы, который использовал бы информацию только о конфигурации электронных оболочек атомов, составляющих систему. Ab-initio, то есть первопринципные методы, из-за высокой степени расчёта, в них применяются некоторые приближения, которые не позволяют применить эти методы к любым системам. При этом точность расчёта в большинстве случаев довольно высока.

Термин ab-initio фактически именует одно из направлений современной теоретической физики твёрдого тела, и означает совокупность физических приближений, процедур вычисления и оптимизации используемых для расчёта электронных и фононных спектров с целью нахождения термодинамических и кинетических характеристик материала, таких, как коэффициент теплового расширения, электрическая проводимость и другие.

Первыми из серьёзных достижений в этом направлении можно считать концепцию самосогласованного поля и уравнения Хартри и их прямые уточнения, уравнения Хартри-Фока. Эти уравнения с различными вариациями являются основой вычислительных методов в квантовой химии. В последнее время всё большее распространение в физике твёрдого тела приобретают методы ab-initio расчётов, основанные на использовании метода функционала плотности. Достоинством расчётов из первых принципов являются точное описание атомного взаимодействия с учётом квантовых эффектов. Недостатком – невозможность расчёта за разумное время систем достаточно большим числом атомов (на практике редко более 100).

К основным методам расчёта из первых принципов можно отнести следующие:

Метод Хартри-Фока и его дальнейшее развитие.

Метод функционала электронной плотности.

33. Теория функционала плотности DFT.

Разработан метод моделирования на основе теории функционала плотности ТФП (DFT). Согласно этой теории все электронные свойства системы, включая энергию, могут быть получены из электронной плотности (без знания волновых функций). Применяют 2 типа ТФП: приближение локальной плотности и приближение локальной спиновой плотности.

Электронная плотность – мера плотности электронного облака в данном месте, плотность вероятности присутствия электронов. Функция определена во всём пространстве.

Интеграл от электронной плотности по всему пространству даёт полное число электронов. Кинетическая энергия электронов описывается явно в приближении независимых частиц, классическая часть потенциальной энергии описывается по закону Кулона. Обмен и электронная корреляция учитываются приближенно.

Электронная корреляция – эффект, обусловленный мгновенным кулоновским отталкиванием между электронами (стремлением электронов избежать друг друга).

Его учёт приводит к более низкому значению полной энергии системы. Указанный эффект не учитывается в методе Хартри-Фока.

Изменение энергии, вызванное этим мгновенным Кулоновским взаимодействием, называется энергией корреляции:

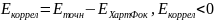
Учёт электронной корреляции особенно важен при исследовании эффектов, зависящих от возбуждённых состояний. Расчёты по ТФП требуют меньше компьютерного времени, чем для вычисления другими неэмпирическими методами, позволяя рассчитывать характеристики молекулярных систем с большим количеством атомов. Основное отличие ТФП от методов ab-initio состоит в том, что система описывает не волновой функцией, а электронной плотностью, определяемой как:

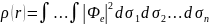
где 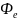– многоэлектронная волновая функция системы, 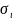– совокупность спиновых и пространственных координат электронов, n – число электронов.

Т.о. 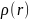есть функция только трёх пространственных координат r в точке, в которой даёт вероятность обнаружения какого-либо из электронов молекулы. Её можно рассматривать как плотность электронного газа, образующего электронное облако молекулы.

Существуют две теоремы: первая теорема – теорема Хоэнберга и Кона – утверждает, что любое свойство основного состояния данной системы описывается только электронной плотностью , и, таким образом, не требует знания волновой функции. Эта теорема доказана только для основного состояния молекулы (ТФП не является точной теорией для возбуждённых состояний).

Вторая теорема устанавливает вариационный принцип в ТФП: если E₀ – точная энергия основного состояния, то для любой другой электронной плотности ρ, которая может быть и приближение к истинной электронной плотности основного состояния, выполняется соотношение:

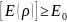
Это утверждение, как и в методах, основанных на волновой функции, даёт метод нахождения 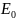и соответствующей плотности. Если любое свойство основного состояния молекулы может быть выражено через ρ, то электронная энергия в ТФП есть:

где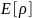 – кинетическая энергия, 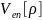– потенциальная энергия электроно-ядерных взаимодействия, 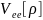– энергия межэлектронных взаимодействий:

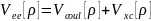
где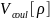 – энергия кулоновского взаимодействия электронов, 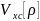– обменно-корреляционная энергия, т.е. та часть потенциальной энергии взаимодействия электронов между собой, которая учитывает обменный член в методе Хартри-Фока и корреляционную энергию.

Функционалы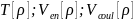 могут быть найдены точно аналогично методу Хартри-Фока. Наиболее простой способ – метод Кона-Шема. В этом методе ρ представляется как сумма вкладов отдельных электронов, описываемых некими вспомогательными самосогласованными орбиталями. Орбиталями Кона-Шема(Kohn-SHN-Sham (KS) orbitals) наз.:

Хотя орбитали Кона-Шема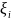 аналогичны орбиталям Хартри-Фока, но не тождественны им, так как оператор энергии для них включает другие компоненты энергии, в том числе корреляционную энергию. Компоненты энергии задаются формулами:

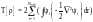
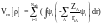
А для обменно-корреляционного потенциала V_xc[ρ], точное представление не известно и требуется введение дополнительных приближений. Наиболее простое из них:

- Приближение локальной плотности(Localdensityapproximation, LDA). Его основная идея состоит в том, что V_xc[ρ] есть энергия, зависящая от локальных свойств однородного электронного газа. Под локальностью какого-то свойства в данной точке понимается его зависимость от ρ только в данной точке. В приближении локальной плотности:

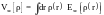(1)

Обменно-корреляционная энергия однородного электронного газа E_xc[ρ(r)] известна в достаточно хорошем приближении. В большинстве случаев используются ее численные приближения в виде таблиц или приближенные формулы.

-Метод LDA может быть сформулирован и дляоткрыто-оболочечных (но невырожденных) систем в основном состоянии. Для этого вводится отдельная плотность для каждой компоненты спина и соответствующие спин-орбитали Кона-Шэма. В такой формулировке метод обычно называют приближение локальной спиновой плотности(Localspindensityapproximation, LSDA).

- Точность метода Кона-Шэма может быть улучшена путем введения поправки в функционал, которая бы зависела не только от плотности в данной точке, но и от градиента этой плотности. Таким образом, хотя функционал и остается локальным, он начинает учитывать и изменение плотности в пространстве. Такой подход называется обобщенным градиентным приближением(Generalizedgradientapproximation, GGA):

(2)

Точность GGA намного выше, чем LDA, поскольку градиент частично учитывает нелокальность электронных взаимодействий. Вычислительные затраты, однако, остаются практически прежними, поскольку зависимость от градиента вводится в предопределенную величину - обменно-корреляционную энергию. По этой причине большинство современных вариантов ТФП основаны именно на приближении GGA.

Различные варианты формулы (1) и (2) приводят к различным вариантам ТФП. Говорят, что ТФП используется с различными функционалами. Наиболее известные и широко используемые среди них функционалы Бекке-Пердью (BP), Пердью-Ванга (PW91), Бекке-Ли-Янга-Парра (BLYP) и Пердью-Бёрке-Эрнцерхофа (PBE).

Часто обменно-корреляционный функционал разбивается на обменную и корреляционную компоненты, причем для каждой компоненты используется свой приближенный функционал. В большинстве случаев их можно комбинировать независимо друг от друга, выбирая один из обменных функционалов и добавляя корреляционный функционал.

Во многих случаях нелокальная обменная энергия описывается локальным обменным функционалом – возникают погрешности. Для того чтобы бороться с ними, было предложено включать в V_xcточный Хартри-Фоковский обменный оператор, рассматривая его как одну из моделей для описания обменной энергии. Оказалось, что такой способ дает значительный выигрыш в точности, особенно, если комбинировать его с некоторыми другими обменными функционалами. Так появилось семейство параметрических функционалов, среди которых наиболее известен B3LYP - функционал, включающий три компоненты обменного функционала, а корреляционная часть представлена комбинацией двух функционалов.

Особенностью этого подхода является то, что три обменные компоненты берутся на основе сравнения с экспериментальными данными. В результате подход приобретает черты полуэмпирического метода. Несмотря на это оказывается, что его точность в большинстве случаев значительно выше, чем в случае методологически «чистых» функционалов. Платой за лучшую точность является увеличение времени расчета (который требует расчета обменных интегралов), в результате чего по времени расчета функционал B3LYP уступает большинству других функционалов.

В настоящее время появилось большое число новых функционалов, точность которых приближается к точности B3LYP, а в ряде случаев и превосходит его. Следует упомянуть функционал OLYP (комбинация обменного функционала OPTX и корреляционного LYP), функционалы HCTH и PBE.

Как только обменно-корреляционный потенциал задан, решение методом ТФП проводится путем решения т.н. уравнений Кона-Шэма:

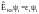(3),

где оператор Кона-ШэмаẾ_KSопределяется в соответствии с вариационным принципом.

Как только система (3) задана, процедура ее решения полностью аналогична процедуре самосогласования метода Хартри-Фока. Разлагая ψ_iпо орбиталям атомного базиса, можно записать уравнения для коэффициентов МО C_ij, т.е. уравнения, аналогичные уравнениям Рутаана.

Тот факт, что в ТФП не требуется расчет обменных интегралов и не нужны специальные методы для уточнения корреляционной энергии приводит к тому, что по вычислительной эффективности ТФП становится одним из наиболее предпочтительных методов. Использование ТФП позволяет рассчитывать большие молекулярные системы (включающих десятки и сотни, а иногда и тысячи атомов) с затратами, сравнимыми с методом Хартри-Фока, а по точности значительно превосходящей его. ТФП может описывать свойства свободных молекул; очень хорошо воспроизводятся свойства комплексов с водородной связью. Важный недостаток ТФП при расчетах основного состояния состоит в том, что эта теория учитывает энергию корреляции только для небольшого диапазона возбуждений. ТФП не может применяться для описания слабосвязанных систем; как правило, занижает энергии переходных состояний слабополярных молекул, в т.ч. органических. Переходные состояния часто включают состояния, которые не описываются ковалентно-связанной ВФ, и применение к ним ТФП означает попытку описания возбужденных или вырожденных состояний.