29. Электронный парамагнитный резонанс

Это явление резонансного поглощения электромагнитного излучения парамагнитными частицами, помещёнными в постоянное магнитное поле. Один из методов радиоспектроскопии. Данный метод используется для изучения систем с ненулевым электронным спиновым магнитным моментом.

Ф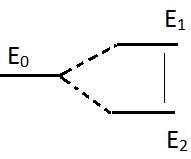 изика явления: в отсутствие постоянного магнитного поля Н магнитные моменты неспаренных электронов направлены произвольно. Состояние системы таких частиц вырождено по энергии. При наложении поля Н проекции магнитных моментов на направление поля принимают определённые значения и вырождение снимается.

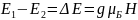
g – фактор спектроскопического расщепления, μ_Б – магнетон Бора.

Основные параметры спектров ЭПР – интенсивность, форма, ширина резонансной линии, g-фактор, константы тонкой и сверхтонкой структуры.

G-фактор:

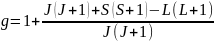
L, S, J – квантовые число соответствуют орбитального, спинового и полного моментов количества движения.

В спектроскопии ЭПР триплетных состояний (S = 1) помимо электро-ядерных взаимодействий (СТВ) необходимо учитывать взаимодействие неспаренных электронов друг с другом.

Техника эксперимента:

К – источник, Р – резонатор, В – детектор, У – усилитель, П- регистрирующее устройство.

Спектрометры обычно работают при частоте 9 ГГц. Длина волны 3,2 см. Магнитная индукция – 0,3 Тл. ЭМИ СВЧ от К по В поступают в объёмный Р.

Чувствительность современных спектрометров достигает 10^-9 метра (10¹¹ частиц в образце). При оптимальных условиях регистрации и ширине линий 10^-4Тл.

Важная характеристика = временная шкала метода, определяемая частотой СВЧ излучения, падающего на образец с частотой 10^-10).

Применение: методом ЭПР можно определить концентрацию и идентифицировать парамагнитные частицы в другом агрегатном состоянии.

ЭПР применяется в радиационной химии, фотохимии, катализе, в изучении процессов окисления и горения т.д.

30. Квантово-химическая модель.

Для описания химической системы необходим учёт множества физических явлений: движение электронов в поле ядер, взаимодействие электронов между собой, релятивистское увеличение массы электронов за счёт ускорения вблизи ядра, квантовые эффекты неопределённости положения и импульса, спиновые и другие эффекты. Поскольку одновременный учёт этих явлений невозможен, используют множество математических моделей, которые учитывают наиболее простые и важные эффекты. Особенностью этих моделей является невозможность их точного аналитического решения.

В отличие от многих простых математических моделей, модели молекулярных систем могут быть решены точно только для тривиальных систем, например, атома Н, молекулярного иона водорода Н²⁺_. Для всех практически значимых химических систем решение соответствующих электронных уравнений возможно только приближенно. При этом точность такого решения определяется не только физическими эффектами, заложенными в математическую модель, но и способом решения уравнения.

Квантово-химическая модель обязана подчиняться 2-м основным принципам:

1. Уникальность решения. Она даёт уникальное (хотя и приближенное) решение уравнения Шредингера для данной конфигурации ядер, электронного и спинового состояния молекулы.

2. Трансферабельность. Она применима к химической системы произвольно размера и с произвольной молекулярной структурой (хотя согласие результатов расчёта с экспериментом и практическая осуществимость такого расчёта может зависеть от конкретных параметров системы).

Кроме того желательно, чтобы при использовании моделирования выполнялись ещё несколько дополнительных принципов:

1. Размерная согласованность – результаты, получаемые для системы, состоящей из 2-х молекул, находящихся от бесконечном расстоянии друг от друга, должны быть точно равны сумме результатов, получаемых для двух изолированных молекул.

2. Воспроизведение точных результатов соответствующей N-электронной задаче.

Квантово-химический метод, явно учитывающий взаимодействия N-электронов должен давать такое решение, которое совпадает с точным решением уравнения Шредингера для N-электронной задачи, допускающей точное (аналитическое) решение.

3. Вариационность – энергия, предсказываемая методом, должна быть верхней границей точного решения электронного уравнения. Более точный метод должен давать более низкое значение энергии, чем его предшественники.

4. Точность – в идеале модель должна давать высокоточные количественные результаты, совпадающие с экспериментом в пределах экспериментальной погрешности. Как минимум, модель должна предсказывать качественные закономерности для групп молекулярных систем.

5. Вычислительная эффективность – расчёты в рамках данной модели должны быть осуществимы с использованием современных компьютерных технологий.