13. Общая и местная система координат. Матрица преобразований (направляющих косинусов)

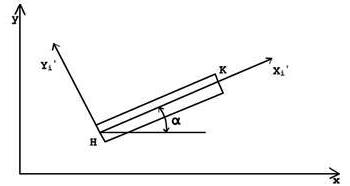
Каждый стержень в конструкции имеет свою ориентацию. Поэтому при расчете вводится понятие  местной , или локальной (связанной с осью стержня)  и  общей   для всей конструкции  сис­тем  координат  Общую  систему  координат  можно также называть глобальная.

На рис. 1 x'i-y'i -  местная , а х-у -  общая  система  координат.

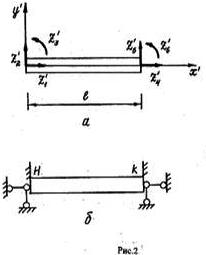
На рис. 2, а изображен конечный элемент в  местной  системе  координат , связанной с его осью, а также отмечены направления узловых перемещений Z₁’, Z₂’, …, Z₆’, являющихся компонентами вектора Zi =(Z₁’ Z₂’ …Z₆’)^T в этой  системе  координат  Местная система  координат  - это такая система координат, в которой ось X направлена вдоль конкретного стержня, а ось Y перпендикулярно. Эта модель имеет форму квадратной матрицы, размером 6х6, схематически обозначается Ri’, где индекс i означает, что это матрица жесткости стержня с номером i, а значок штриха наверху означает, что  система  координат  предполагается  местная  (локальная).  В  общем  виде матрицу Ri’ можно представить следующим образом:

Поскольку стержни в конструкции могут быть расположены произвольным образом, возникает необходимость перехода от матрицы   жесткости Ri`, построенной в  местной  системе  координат  к матрице жесткости R_i, определенной в  общей  системе  ко­ординат . Преобразование можно произвести по следующей фор­муле:

В формуле матрица V представляет собой матрицу перехо­да из одной ортогональной  системы  координат  в другую.

Мы получаем математическую модель одного (любого) стержня произвольной плоской стержневой конструкции в  общей  системе   координат. Она представляет собой матрицу, размером 6х6, схематически обозначается Ri, получить ее можно в результате матричной операции  (4).  

Рассмотрим теперь КЭ в составе рамы, расположенный под углом а к оси X в

общей системе осей координат.

Необходимо перейти от матрицы реакций [r] j в местной системе осей координат к матрице [г] в общей системе координат.

Задачу решаем следующим образом. В начале построим матрицу [c]j, которая преобразует перемещения КЭ {z}_] в общей системе осей координат в перемещения {v}j, по выражению

{v}_j = [c]_j {z}_j

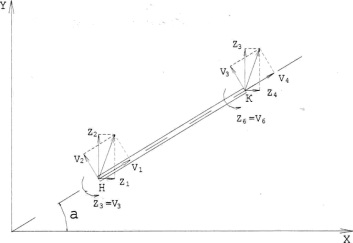
V₁ = Z₁ cosa + Z₂ sina

V₂ = -Z₁ sina + Z₂ cosa

V₃ = Z₃

V₆ = z₆

V₄ = Z₄ cosa + Z₅ sina

V₅ = -Z₄ sina + Z₅ cosa

В матричной форме приведенная выше запись будет иметь вид

или в блочной форме

где для жесткого узла

для шарнирного узла

Так как мы рассматриваем плоские упругие системы, то векторы узловых усилий и узловых перемещений, как для отдельного элемента, так и для сооружения в целом, связаны между собой линейно

{S}'_j =[r]_j'{V}_{j -} в местной системе осей координат.

{S}_j=[r]_j{Z}_{j -} в общей системе осей координат

Кроме того

{V}_J = [c]_J{Z}_J,

Аналогично

{S}_j '= [c]_j{S}_j,

где {S}' ,{S}-узловые усилия КЭ соответственно, в местной и общей системах осей координат. Тогда

{S}_j = [с]_j^-1 {S}_j = [c]_j^-1 [r]_j' {V}_j= [c]_j^-1 [r]_j ^'[c]_j{Z}_j

Для матрицы направляющих косинусов выполняется равенство

[c]_j^-1 =[c]_j^T

Тогда {S}_j = [c]_j^T [r]_j ^'[c]_j{Z}.

Обозначим

[r]_j = [c]_j^T[r]_j ^'[c]_j - это выражение и является формулой для вычисления матрицы жесткости КЭ в общей системе осей координат.

При формировании матриц жесткости отдельных элементов [r]_j' должны быть зафиксированы начало и конец каждого стержня, так как от этого зависит знак угла а, определяющего ориентацию стержня в общей системе осей координат XOY.