1)Полная система уравнений строительной механики. Полная система уравнений состоит из статических(уравнения равновесия), геометрических(уравнения связи между перемещениями и деформациями) и физических(плоское напряженное состояние, плоская деформация) уравнений. Стержневая система находится в равновесии тогда, когда уравновешены как ее стержни, так и узлы. -статическое уравнение равновесия. Где -матрица уравнения равновесия; -вектор внутренних усилий; - вектор внешних сил. Уравнения связывающие перемещение в узлах с деформациями стержней являются геометрическими уравнениями. -геометрическое уравнение. Где -матрица перемещений; -вектор перемещений системы под действием внешних усилий; -вектор деформации системы. Физическое уравнение характеризует плоское напряженное состояние и плоскую деформацию. -физическое уравнение. Где -матрица деформаций; -вектор внутренних усилий; -вектор заданных деформаций(за счет неточности изготовки детали и действия температуры).

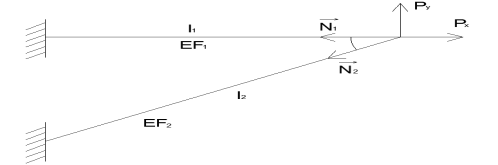
2)Уравнения равновесия. Матрица уравнений равновесия. Стержневая система находится в равновесии тогда, когда уравновешены как ее стержни, так и узлы. В стержнях фермы при узловой нагрузке возникают только продольные силы.

Составим уравнения равновесия для узла 1

;

Запишем систему в матричной форме: , где

-матрица уравнений равновесия.

-вектор внутренних сил; -вектор внешних сил. ;

-матрица напряжений.

m-столбцы; n-строки. Если n>m, то система геометрически изменяема. Если n=m, то система статически определима. Если n<m, то система статически неопределима.

3) Геометрические уравнения. Принцип двойственности.Стержневая система, соединенная в узлах, должна оставаться соединенной в этих же узлах и после деформации. Уравнения, вы­ражающие это положение, называются уравнениями совместности.

На рис. 8.8, а, б показаны деформации системы соответственно при смещении узла 1 на U и на V. Ввиду малости перемещений перемещения по окружности заменены пере­мещениями по касательной к окружности (по перпендикуляру к стержню).

Итак,

Рис. 8.8а,б

Перенеся правые части выражения (8.19) в левую и записывая полученные уравнения в матричной форме, получим

Уравнения (8.20) связывают перемещения узла (U, V) с деформа­циями стержней Δ₁ ,Δ₂,. и являются геометрическими уравнениями для системы.

Применять для получе­ния уравнений совместнос­ти, приведенные выше геометрические построения для системы с большим коли­чеством узлов очень слож­но. Более удобно исполь­зовать для этого так назы­ваемый принцип двойствен­ности. Дня этого рассмот­рим стержневую систему, имеющую n узлов и m стержней. Все силы, действующие на стержневую систему, делятся на внешние и внут­ренние. К i-му жесткому узлу плоской стержневой системы мо­гут быть приложены три силы: Р^x_i—вдоль оси Х ,P^Y_i—вдоль оси У; Mi—момент, приложенный к i-му узлу. Совокупность сил Р^x_i, P^Y_i , Mi образуют вектор сил, приложенных к i-му узлу:

Совокупность всех внешних сил, действующих на n узлов, мо­жет быть представлена в виде

Внутренние силы, действующие в стержне, полностью определяются тремя силами: N_j, M_Hj, M_Kj которые можно характеризовать вектором

Совокупность всех внут­ренних сил, действующих во всех стержнях, может быть пред­ставлена в виде

Векторы S и Р не являются независимыми векторами, а связаны между собой урав­нениями равновесия узлов (1)

Каждый жесткий узел может иметь три перемещения: U_i — вдоль оси Х, V_i—вдоль оси У; φ_i— поворот.

Совокупность пере­мещений U_i, V_i, φ_i образует вектор перемещений i-го узла :

Очевидно, что работа внешних сил, приложенных к i-му узлу, равна скалярному произведению вектора внешних сил Р_i на век­тор перемещений того же узла Z_i с коэффициентом ½: Второе произведение является матричной записью скалярного произведения. Аналогично для всей стержневой системы можно записать Итак, каждому вектору внешних сил Р соответствует вектор перемещений Z таким образом, чтобы их скалярное произведение давало работу. Подобные векторы в последующем будем назы­вать двойственными векторами.

Запишем выражение для работы внутренних сил в i-м стержне

где As-работа внутренних сил в i-м стержне; Δ— вектор де­формаций i-го стержня.

Вектор Sj имеет вид , Δj -

Запишем выражение для работы внутренних сил для всей системы

Аналогично предыдущему, векторы S н Δ являются двойст­венными. Очевидно, что из условия совместности деформаций система стержней, объединенная узлами до деформации, остается такой же системой, объединенной теми же узлами и после де­формации (можно по заданному вектору перемещений узлов Z найти вектор деформаций стержней Δ). Запишем эту связь в виде (2)

где A₁— матрица, связывающая перемещения с деформациями.

В силу закона сохранения энергии работа внешних сил равна работе внутренних сил:

A_P = A_S или (3)

Выражая из уравнения вектор Р и вектор Δ и подставляя эти значения в выражение получим (5)

Соотношение(5)соблюдается при любом Z, удовлетворяющем кинематическим граничным условиям, следовательно, (4)

Таким образом, если два вектора (S,P) удовлетворяют соот­ношению (1), а двойственные им векторы (Δ,Z) — соотношению (2), причем их скалярные произведения равны (3), то соблюдается равенство (4). Это и есть принцип двойственности.

4.Закон гука. Физические уравнения

Для любой стержневой системы можно составить статические и геометрические уравнения.

В случае системы с жесткими узлами первая система содержит 3n уравнении, а вто­рая Зm (n — число узлов, m —число стержней), полное число уравнении равно 3(n+m). В эти уравнения в качестве неизвестных входят векторы S (3m), Z (Зп) и Δ (3m); полнoе количество неизвест­ных составляет 3 (п+ 2m). Таким образом, количество неизвестных превышает число уравнений. Для решения задачи необходимо построить еще 3m уравнений.

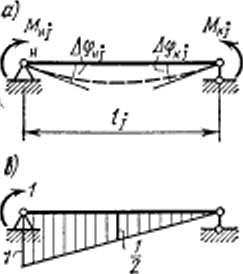
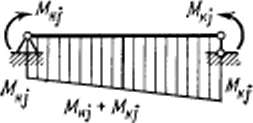
Рис. 8. 10

Запишем закон Гука для i-го стержня. В случае действия продольной силы имеем

Рассмотрим случай действия моментов М_нi, и М_ki (рис. 8.10.а). Используя метод Мора, определим Δφ_нi и Δφ_ki .Построим гру­зовую (рис. 8.10,6) и единичные эпюры (рис. 8.10,«, г) и пере­множим их между собой, воспользовавшись формулой Симпсона:

Перепишем зависимости в матричной форме: (1)

В случае, если стержень имеет по концам шарниры, то

Аналогично, если стержень имеет один шарнир (либо М_нi=0 или М_ki=0), то

Соотношение(1) справедливо для одного стержня. Придавая индексу i значение i= 1, 2, .... m, получим соотношение Гука для всей стержневой системы. В матричной форме закон Гука для всей стержневой системы имеет вид

7. Основные законы и методы вычислительной механики.

Строительная механика на современном этапе развития располагает большим арсеналом методов расчета как дискретных систем (например, состоящих из стержней), так и континуальных (сплошных) конструкций и их элементов, таких как пластины, плиты, оболочки, массивы.

Расчет напряженно-деформированного состояния дискретной конструкции, как правило, приводит непосредственно к решению систем алгебраических уравнений. Пример этому – широко применяемые при расчете плоских и пространственных стержневых систем классические методы сил и перемещений.

Для расчета континуальных систем используются более сложные математические модели и соответственно численные методы. Так, основные зависимости между геометрическими и физическими величинами в механике сплошных сред выводятся с помощью элемента бесконечно малых размеров. Соотношения между средними значениями этих величин, предполагая их непрерывность, распространяются с бесконечно малых элементов на всю рассматриваемую область. Таким образом, появляются дифференциальные, интегральные или интегро-дифференциальные уравнения, вместе с граничными и начальными условиями они образуют математическую модель соответствующей задачи. К сожалению, точное решение в аналитической форме прикладных континуальных задач возможно лишь в очень немногих случаях, поэтому особо важное значение приобретают приближенные, но достаточно общие методы их решения. В последние десятилетия эти методы, называемые также численными, получили особенно активное развитие в связи с применением в инженерной практике современных вычислительных средств.