1. Элементы строки новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, делённая на разрешающие элементы.

2. Все элементы столбца в новой таблице равны 0, за исключением разрешающего элемента, который равен 1.

3. Все остальные элементы находятся по «правилу прямоугольника». Произведение главной диагонали минус произведение побочной диагонали, делённое на разрешающий элемент.

Для контроля вычислений элементов индексной строки применяются формулы и .Альтернативный оптимум (признак бесконечности множества оптимальных планов): если в индексной строке последней симплексной таблицы (содержащей оптимальный план), имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача линейного программирования имеет бесконечное множество оптимальных планов.Признак неограниченности целевой функции: если в разрешающем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена.

3. Решить задачу линейного программирования графическим методом.

1)6x1-5x2>=17 42-5x2=17 72-5x2=17

X1	7	12
X2	5	11

5X2=25 5x2=55

X2=5 x2=11

2)x1+2x2<=34 14+2x2=34 12+2x2=34

X1	14	12
X2	10	11

2X2=20 2x2=22

X2=10 x2=11

3)-4x1+9x2>=17 -28+9x2=17 -64+9x2=17

X1	7	16
X2	5	9

9X2=45 9x2=81

X2=5 x2=9

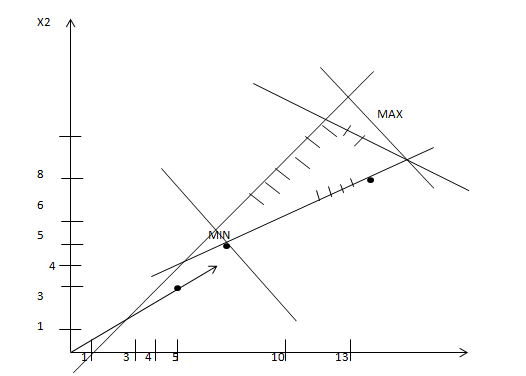
MIN(7;5);MAX(16;9);

f(x)=5*7+3*5=50-MIN

f(x)=16*5+9*3=107-MAX

Вариант 5

1. Понятие модель. Принципы моделирования,

Модель – это упрощённое представление о реальном объекте, процессе или явлении.Модель – это, как правило, искусственно созданный объект в виде схемы математических формул, физической конструкции, наборов данных и алгоритмов и их обработки.

Моделирование – это метод познания, состоящий в создании и исследовании моделей.

Основные этапы моделирования:

1. Постановка задачи.

Определяются цели анализа. Вырабатывается общий подход к исследуемой проблеме. Требуется глубокое понимание сущности поставленной задачи.

2. Изучение теоретических основ и сбор информации об объекте-оригинале.

Подбирается и разрабатывается подходящая теория, если её нет – устанавливаются причинно-следственные связи между переменными, описывающими объект. Определяются входные и выходные данные. Принимаются упрощённые положения.

3. Формализация составление математической модели).Выбор системы условных обозначений. С их помощью записываются отношения между составляющими объекта в виде математических выражений. Устанавливается класс задач, к которым может быть отнесена полученная математическая модель. Значения некоторых параметров могут быть конкретизированы.

4. Выбор метода решения.На этом этапе устанавливаются окончательные параметры модели. Выбирается какой-либо метод решения или разрабатывается специальный метод.

5. Реализация модели.

Разрабатывается алгоритм. Пишется программа, которая отлаживается, тестируется и получает решение исходной задачи.

6. Анализ полученной информации.

Сопоставляется полученное и предполагаемое решение. Проводится контроль погрешности моделирования.

7. Проверка адекватности реальному объекту.Результаты, полученные по модели, сопоставляются либо с имеющейся об объекте информации, либо проводится эксперимент и его результаты сопоставляются с расчётами.

2 Симплекс-метод.

Пусть в системе ограничений имеется единичный неотрицательный базис . Говорят, что ограничение канонической задачи линейного программирования имеет предпочтительный вид, если при неотрицательности его правой части ( ) левая часть содержит переменную с коэффициентом равным 1, а в остальных ограничениях с коэффициентом равным 0. Если каждое ограничение в канонической задачи линейного программирования имеет канонический вид, то начальный опорный план строится следующим образом: предпочтительные переменные выбираются в качестве базисных, а все остальные – свободные. Свободные переменные приравниваются к 0, а базисные переменные – к свободным членам.