2. Транспортная задача. Метод минимального элемента.

Метод наименьшего элемента

Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.

Алгоритм:

Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.

Проверяются строки поставщиков на наличии строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены. Такие столбцы и строки далее не рассматриваются.

Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.

3. Решить задачу линейного программирования графическим методом.

1)x1+4x2<=53 13+4x2=53 9+4x2=53

X1	13	9
X2	10	11

4X2=40 4x2=44

X2=10 x2=11

2)x1-x2<=3 4-x2=3 5-x2=3

X1	4	5
X2	1	2

-X2=-1 -x2=-2

X2=1 x2=2

3)7x1+3x2<=71 56+3x2=71 35+3x2=71

X1	13	9
X2	10	11

3X2=15 3x2=36

X2=5 x2=12

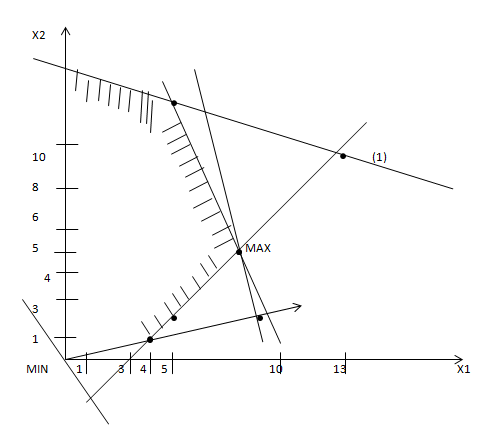
MIN(0;0); MAX(8;5)

f(x)=9*0+2*0=0-MIN

f(x)=9*8+2*5=82-MAX

Вариант 4

1. Математическая модель злп.

Построить таблицу по данным. Составляем систему ограничения. План x=(x1,x2), удовлетворяющий системе ограничений и условию неотрицательности называется допустимым. Допустимый план, для которого целевая функция принимает максимальное значение, называется оптимальным.

Линейная функция, максимум которой надо определить, вместе с системой ограничений и условием неотрицательности образуют математическую модель задачи. Так как целевая функция линейная, а система ограничений содержит только линейные ограничения, то данная задача является задачей линейного программирования

2. Заполнение симплексных таблиц.

Приведя модель задачи к предпочтительному виду, её заносят в симплексную таблицу. В столбец БП занесены базисные переменные. Столбец Сб содержит коэффициенты целевой функции, стоящие при базисных переменных. Столбец А₀ содержит свободные члены. Сверху, над рабочей частью таблицы, указаны все переменные и коэффициенты целевой функции . Последняя строка таблицы называется индексной или строкой оценок. Рассмотрим переход к не худшему опорному плану на примере задач линейного программирования на максимум. Приведём её к каноническому виду и занесём в симплексную таблицу. Если все , то начальный опорный план оптимален. Если же существует , то план не оптимален. При определённых условиях, его можно улучшить. Среди отрицательных оценок находят максимальную по абсолютной величине. Столбец , определённый этой оценкой, называется разрешающим. Если задача решается на минимум, то из положительных выбирается максимальное значение. Переменную , соответствующую разрешающему столбцу, следует ввести в базис. Для определения переменной, выводимой из базиса находят отношение . Такие отношения называются симплексными. Среди симплексных значений находят … оно укажет строку, в которой содержится исключаемая из базиса переменная . Строка , соответствующая минимальному симплексному отношению, называется разрешающей. На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент. Новая таблица строится по следующим правилам: