Вариант 1.

1. Транспортная задача. Метод потенциалов.

Используется для построения оптимального плана по опорному плану, который можно найти с помощью 3 методов: метод северо-западного угла, метод минимального элемента, метод Фогеля, у которого число занятых клеток равно n+m-1 каждому поставщику и каждому потребителю ставится в соответствии число называемое потенциалом. Потенциалы выбираются так, что бы их сумма для каждой загруженной грузом клетки была равна тарифу перевозки единицы груза. Так если клетка (I;k) базисная, то ui+vk=Cik где, ui- потенциал iго поставщика, vk- потенциал k-го потребителя, Cik – тариф базисной клеткик.

Далее вычисляюся оценки клеток . Sij=Cij-(ui+vj)

Если все оценки для свободных клеток Sij >=0, то полученный опорный план перевозов оптимальный, при наличии хотя бы одной оценки Sij меньше 0, то в число базисных входят в клетку для которых Sij минимальная. Для такой клетки строится цикл и производится перемещение груза, так что бы баланс цикла сохранялся .

2. Этапы компьютерного моделирования.

1) Постановка задачи.

Под задачей понимается некая проблема, которую надо решить. На этапе постановки задачи необходимо: а) Описать задачу; б) Определить цель моделирования; в) Проанализировать цель или процесс;

2)Разработка модели. Информационная модель. На этом этапе выясняются свойства, состояние, действия и другие характеристики элементарных объектов в любой форме: устно, в виде схем, таблиц.

Знаковая модель. Прежде, чем приступить к процессу моделирования человек составляет информационную модель в той или иной знаковой форме, которая может быть компьютерной или некомпьютерной.

Компьютерная модель – модель, реализованная средствами программной среды.

3) Компьютерный эксперимент. Компьютерный эксперимент включает некоторую последовательность работы с моделью, совокупность целенаправленных действий пользователя над компьютерной моделью.

4) Анализ результатов моделирования. Конечная цель моделирования- принятие решения которое должно быть выработанное на основе всестороннего анализа получения данных.

3. Решить задачу линейного программирования графическим методом.

1)-x1+x2<=3 -1+x2=3 -3+x2=3

X1	1	3
X2	4	6

X2=3+1 x2=3+3

X2=4 x2=6

2) 5x1+3x2<=97 55+3x2=97 85+3x2=97

X1	11	17
X2	14	4

3X2=42 3x2=12

X2=14 x2=4

3)x1+7x2>=77 x1+70=77 x1+63=77

X1	7	14
X2	10	9

X1=10 x1=14

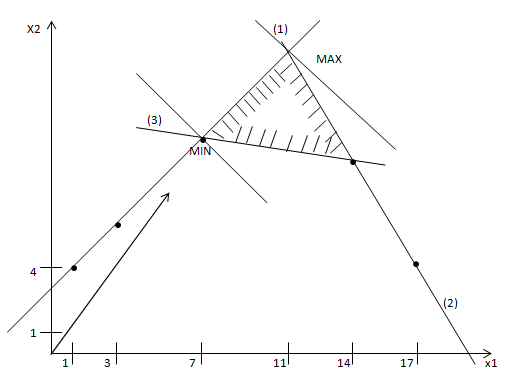
MAX=(11;14);MIN(7;10)

f(x)=3*11+4*14=89-MAX

f(x)=3*7+4*10=21+40=61-MIN

Вариант 2

1. Транспортная задача. Метод Фогеля.

Согласно условию задачи составим таблицу. (тарифы c_ij располагаются в нижнем правом углу ячейки) В каждой строке, найдем разность  _i между двумя ячейками (доступными для выбора) с наименьшими тарифами. В каждом столбце, найдем разность  _j между двумя ячейками (доступными для выбора) с наименьшими тарифами. Из полученных разностей выберем наибольшую. Пишем сколько надо потребителю, вычеркивает строку и столбец если больше ничего не надо. Опять ищем разность между между ячейками столбцов и строк. И так будем продолжать пока не заполним количество ячеек которые можно проверить по формуле r=m+n-1