1. Генеральная совокупность и выборка, вариационный ряд, полигон частот, гистограмма, эмпирическая функция распределения.

Ответ:

Одним из видов статистического наблюдения является выборочное наблюдение. При осуществлении выборочного наблюдения исследуются не все единицы статистической совокупности, а некоторая специальным образом отобранная часть этой совокупности. В данном случае вся статистическая совокупность называется генеральной совокупностью, а часть генеральной совокупности, отобранная для проведения наблюдений, называется выборочной совокупностью (выборкой) или подсовокупностью. Целью выборочного наблюдения является: характеристика выборочной совокупности системой статистических показателей, и перенесение выводов, сделанных на основе наблюдений за выборочной совокупностью на всю, возможно бесконечно большую генеральную совокупность.

Анализ данных, полученных в результате выборочных наблюдений, обычно подразумевает решение следующих задач:

• графическое изображение результатов наблюдений (в виде гистограммы распределения, полигона распределения, эмпирической функции распределения);

• расчет комплекса выборочных характеристик (описательных статистик): центра группирования; рассеяния; формы распределения выборки;

• выдвижение и проверка статистических гипотез относительно закона распределения генеральной совокупности;

• построение интервальных оценок для параметров распределения генеральной совокупности.

Результаты статистических сводок и группировок могут быть представлены в виде татистических рядов – упорядоченных совокупностей значений показателей (статистического признака). По своему содержанию статистические ряды подразделяются на ряды динамики и ряды распределения.

Рядом динамики называют систематизированную совокупность числовых данных, характеризующих изменения изучаемых явлений во времени.

Ряд распределения, представляет собой систематизированную последовательность статистических единиц, сгруппированных по конкретному признаку. Он характеризует состав изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения статистических единиц. Обычно ряд распределения представляет собой результат структурной группировки.

Для различных статистических признаков строятся ряды распределения разного типа:

• атрибутивные – строятся по описательным признакам в порядке возрастания или убывания наблюденных значений признака; примером атрибутивных рядов могут служить распределения населения по национальности, по профессиям, по полу; распределение предприятий по формам собственности;

• вариационные - строятся по количественным признакам, например, распределение рабочих по уровню квалификации, по заработной плате, распределение студентов по успеваемости.

Вариационные ряды делятся на дискретные и интервальные.

В дискретных рядах признак принимает только целые значения, например, размер семьи, тарифный разряд.

Интервальные ряды основаны на непрерывных признаках, принимающих любые, в том числе и дробные значения. В зависимости от того, какая структурная группировка лежит в основе интервального ряда, различают равноинтервальные и неравноинтервальные ряды.

В равноинтервальных рядах ширина интервала является величиной постоянной, в неравноинтервальных – она различна для разных групп.

Исходной частотной характеристикой любого ряда распределения является частота n_i . На ее основе можно рассчитать следующие характеристики:

Частость – удельный вес (доля) единиц совокупности, имеющих определенное значение признака, т. е. это частота, выраженная в виде относительной величины.

Накопленная частота – число единиц совокупности, у которых значение признака не превышает данного x* , т. е. это частота нарастающим итогом.

Накопленная частость – удельный вес (доля) единиц, у которых значение признака не превосходит данное x* , т. е. это частость нарастающим итогом.

Графики и диаграммы являются наглядной формой отображения рядов распределения.

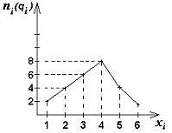
Полигоном распределения называется ломаная линия, соединяющая точки с координатами

или , где x_i - дискретное значение признака, n_i - частота, q_i - частость.

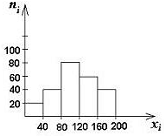
Гистограмма представляет собой ступенчатую фигуру, состоящую из прямоугольников, основания которых равны ширине интервала h_i, а высота - частоте n_i или частости q_i

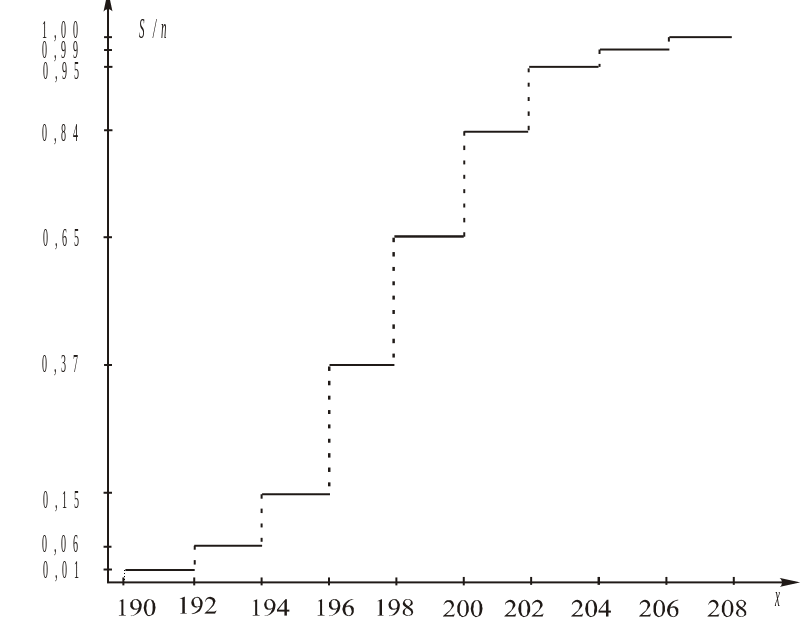
Построение эмпирической функции распределения осуществляется по следующим правилам. В прямоугольной системе координат по оси абсцисс откладывают значения границ интервалов, а по оси ординат значения, соответствующие сумме частот наблюдений, попавших в данный и все предыдущие интервалы, деленной на общее количество наблюдений (накопленная частость). Имеет ступенчатый вид. Примеры на рисунках ниже.

Полигон	График эмпирической функции распределения
Гистограмма