2.3. Новые методы обоснования рациональных решений.

Для использования экономико-математических методов в плани­ровании необходимо экономический объект или процесс записать с помощью математических зависимостей (уравнений, неравенств и т.п.). Этот процесс называется составлением модели.

Математическая модель – это система выражений, описываю­щих характеристики объекта моделирования и взаимосвязи между ни­ми. Процесс моделирования заключается в построении моделей, кото­рые облегчают изучение свойств планируемых процессов и объектов.

Во внутрифирменном планировании наиболее широкое приме­нение нашли следующие экономико-математические методы:

• методы теории вероятности;

• методы математического программирования;

• методы имитации;

• методы теории графов.

Рассмотрим перечисленные методы.

1. Модели, основанные на использовании теории вероятности и математической статистики (стохастические модели)

Методы теории анализа корреляций и регрессий, дисперсион­ного анализа применяются в планировании для анализа различных статистических связей и установления нормативов (трудовых, сто­имостных, материальных).

Методы теории массового обслуживания используются при планировании оптимальных соотношений между размерами ос­новного и вспомогательного производства, а также другими струк­турными элементами предприятия, если процессы в них носят не­регулярный характер и могут быть представлены как процесс мас­сового обслуживания.

Методы теории игр и теории статистических решений при­меняются при принятии и оптимизации решений по управлению процессами взаимоотношения с рынком, страхованию от стихий­ных бедствий, созданию сезонных запасов ресурсов и т.д.

Адаптивное дерево поиска показывает возможные решения, подлежащие рассмотрению (Рисунок 2.4).

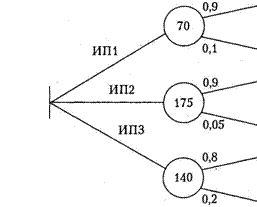
Рисунок 2.4 – Пример составления «дерева решений»

2. Методы математического программирования. Они позволяют выбрать совокупность чисел, являющихся переменными в уравнениях и обеспечивающих экстремум некоторой функции при ограничениях, определяемых условиями работы планируемого объекта.

3. Методы имитации. Имитация представляет собой гибкий и продуктивный метод решения задач, получивший распространение на всех уровнях пла­нирования – от стратегического до оперативно-календарного пла­нирования.

Имитация – достаточно сложный процесс, который зависит от специфики моделируемого объекта. Например, имитация возмож­ных результатов капитальных вложений в процессе их планирова­ния включает следующие этапы:

На рисунке 2.5 приведена кривая вероятностного распределения доли рынка.

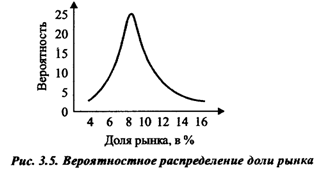
Рисунок 2.5 – Вероятность распределения доли рынка

Из таблицы 2.1 видно, какой процент ситуаций приходится на тот или иной интервал значений нормы прибыли на вложенный капитал.

Таблица 2.1 – Результаты имитирования реальной ситуации капитальных вложений

Норма прибыли на капиталовложения, %	Процент ситуаций – вероятность наступления	Кумулятивная величина вероятностей
30-40	5	5
20-30	19	24
10-20	33	57
0-10	21	78
-10-0	14	92
-30 – -10	8	100

5) Построение кривой риска на основе кумулятивной величины вероятностей (Рисунок 2.6).

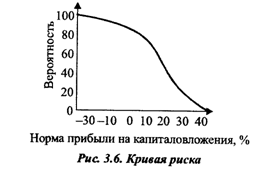
Рисунок 2.6 – Кривая риска

Из рисунка 2.6 и таблицы 2.1 видно, например, что вероятность получе­ния прибыли на планируемые капитальные вложения составляет 78 %, а вероятность того, что они окажутся убыточными, равна 22 %. Имеется 5 шансов из 100, что норма прибыли составит 30-40 %.

Подобная модель позволяет управляющим в ситуации, пред­ставленной графиком на рисунке 2.7, достичь гораздо большей ста­бильности (Рисунок 2.8) в работе.

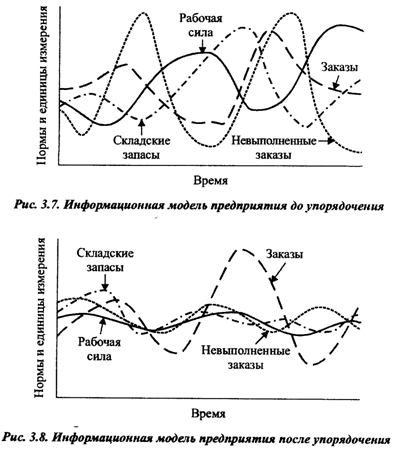
Рисунок 2.7 – Информационная модель предприятия до упорядочения

Рисунок 2.8 – Информационная модель предприятия после упорядочения

Широкое распространение в планировании получил метод Монте-Карло, особенно при анализе риска. Этот метод имитации применим для решения почти всех задач при условии, что альтер­нативы могут быть выражены количественно. Построение модели начинается с определения функциональных зависимостей в реаль­ной системе, которые впоследствии позволяют получить количес­твенное решение, используя теорию вероятности и таблицы слу­чайных чисел.

В таблице 2.2. представлены результаты решения задачи на осно­ве имитационной модели Монте-Карло, в которой интервалы меж­ду прибытием клиентов и временем обслуживания представлены последовательностью случайных чисел. Для интервалов между прибытиями выберем следующую слу­чайную последовательность: 0, 1,2, 3, 4, 5, 6, 7, 8 или 9.

Таблица 2.2 – Решение задачи обслуживания с применением метода Монте-Карло

Номер образца	Первая случайная цифра	Интервал до прибытия, мин	Время прибытия	Время начала обслуживания	Вторая случайная цифра	Время до обслуживания, мин	Время окончания обслуживания	Время ожидания, мин	Время простоя, мин
1	2	3	4	5	6	7	8	9	10
1	-	-	0	0	2	10	10	0	0
2	1	10	10	10	8	30	40	0	0
3	9	20	30	40	6	10	50	10	0
4	8	20	50	50	7	10	60	0	0
5	8	20	70	70	9	30	100	0	10
6	2	10	80	100	4	10	110	20	0
7	0	10	90	110	1	10	120	20	0
8	7	20	110	120	3	10	130	10	0
9	4	20	130	130	4	10	140	0	0
10	9	20	150	150	9	30	180	0	10

Примечание.   Колонка 8 = колонка 5 + колонка 7,

 колонка 9 = колонка 5 - колонка 4,

 колонка 10 = колонка 5 - цифра в предшествующем ряду колонки 8.

4. Метод оценки и пересмотра планов (ПЕРТ) В процессе оптимизации плановых решений применяется класс моделей, основанный на математической теории графов. Частным видом таких моделей являются модели сетевого плани­рования.

В зависимости от точности определения продолжительности работ модели сетевого планирования разделяются на:

• детерминистические;

• стохастические.

Система ПЕРТ может быть реализована в нескольких вариантах:

• ПЕРТ/время;

• ПЕРТ/затраты.

1) ПЕРТ/время. Этот метод планирования имеет четыре отли­чительные особенности: сетевой график, временные оценки, опре­деление резервов времени и критического пути, принятие в случае необходимости оперативных мер по корректировке графика.

2) ПЕРП/затраты. Этот метод представляет собой дальнейшее развитие метода ПЕРТ/время в направлении оптимизации сетевых графиков по стоимости. Для метода ПЕРТ/затраты характерны сле­дующие основные этапы:

1. Структурный анализ работ по проекту.

2. Определение видов работ.

3. Построение сетевых графиков.

4. Установление зависимостей между продолжительностью ра­бот и их стоимостью.

5. Периодическая корректировка сети и оценок.

6. Контроль за ходом работ.

7. Проведение при необходимости мероприятий, обеспечиваю­щих выполнение работ по плану.