ЛИНЕЙНАЯ.

1)Дать определение векторам , доказать необход. и дост. условия коллинеарности двух векотров.

Вектором называется направленный отрезок. Таким образом, вектор - это отрезок, у которого выделен один конец, называемый концом вектора. Этот конец на рисунке обозначается стрелкой. Другой конец отрезка называется началом вектора.

Необходимое и достаточное условие коллинеарности двух векторов.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.

2)Дать определение скалярного произведения векторов и сформулировать его основные св-ва.

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Свойства скалярного произведения

Коммутативность: a · b = b · a .

Дистрибутивность: a · (b + c) = a · b + a · c .

Сочетательность (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b)

Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|2 (норма вектора).

3)Доказать необход. и дост. условия перпендикулярности двух векторов.

Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам (  радиан).

Теорема.

Для перпендикулярности двух ненулевых векторов   и   необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство  .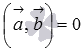

Доказательство.

Пусть векторы   и   перпендикулярны. Докажем выполнение равенства  .

По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы   и   перпендикулярны, то угол между ними равен девяноста градусам, следовательно, 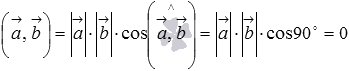 , что и требовалось доказать.

Переходим ко второй части доказательства.

Теперь считаем, что  . Докажем, что векторы   и   перпендикулярны.

Так как векторы   и   ненулевые, то из равенства 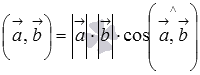  следует, что 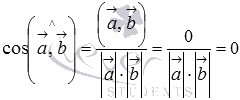 . Таким образом, косинус угла между векторами  и   равен нулю, следовательно, угол   равен  , что указывает на перпендикулярность векторов   и  .

Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.

4) Вывести формулу нахождения скалярного произведения двух векторов заданными своими координатами.

Скалярным произведением двух ненулевых векторов   и  называется число, равное произведению длин этих векторов на косинус угла между ними:

5) Дать определение 2-ого и 3-его порядка, сформулировать их основные св-ва.

Определители 2-го порядка.Св-ва.Определители 2-ого и 3-го порядков Любые 4 числа, расположенные в виде квадратной таблицы, называются квадратной матрицей второго порядка. Каждой квадратной матрице 2-ого порядка можно поставить в соответствие число, называемое её определителем и обозначаемое D=|A|.Определители n-ного порядка.Определитель n-ого порядка равен сумме произведений элементов 1-ой строки на их алгебраические дополнения (A_ij соответствующее элементу a_ij и равно Aij = (-1)^i+j*M_ij) Результат разложения не зависит от того, по какой строке (столбцу) производится разложение:

2 -1 0

4 0 3 = (3 столбец) =

-2 4 5

Свойство1. Важным свойством определителей является следующее соотношение: det A = det A^T;

Свойство 2.det ( A  B) = det A  det B.Свойство 3. det (AB) = detAdetB

Свойство 4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.Свойство 5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.Определение: Столбцы (строки) матрицы называютсялинейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d₁  d₂ , e = e₁  e₂ , f = f₁  f₂ , то верно: 

6)Дать определение векторного произведения двух векторов, сформулировать основные их св-ва.

Определение

Векторным произведением неколлинеарных векторов ~a и ~b называется вектор ~c такой, что |~c| = |~a|* |~b| *sin (~ad;~b), вектор ~c ортогонален к векторам ~a и~b и тройка векторов (~a;~b;~c) — правая. Векторное произведение коллинеарных векторов по определению равно нулевому вектору. Векторное произведение векторов ~a и~b обозначается через ~a *~b или [~a;~b]

Свойства векторного произведения

1. антикоммутативность  ;

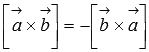2. свойство дистрибутивности   или  ;

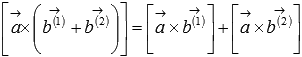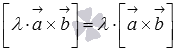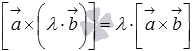3. сочетательное свойство   или  , где 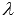  - произвольное действительное число.

7)Вывести формулы для вычисления векторного произведения векторов заданными своими координатами.

8)Дать определение смешанного произведения 3-ех векторов и вычислить его геометрический смысл( рисунок).

Смешанным произведением трёх векторов   называют число, равное  . Обозначается  . Здесь первые два вектора умножаются векторно и затем полученный вектор   умножается скалярно на третий вектор  . Очевидно, такое произведение есть некоторое число.

Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е.  .

Таким образом,   и  .

Д оказательство. Отложим векторы   от общего начала и построим на них параллелепипед. Обозначим   и заметим, что  . По определению скалярного произведения

. Предполагая, что   и обозначив через hвысоту параллелепипеда, находим  .

Таким образом, при 

Если же  , то   и  . Следовательно,  .

Объединяя оба эти случая, получаем   или  .

Из доказательства этого свойства в частности следует, что если тройка векторов  правая, то смешанное произведение  , а если   – левая, то  .

9)Вывести формулы для вычисления смешанно произведения 3-ех векторов, заданными своими координатами.

Проще всего смешанное произведение находится, когда известны координаты векторов. Для вычисления используется формула  .

10) Доказать необход. и дост. условия коллинеарности 3-ех векторов.

Два вектора   и   трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы   и   соответственно. Проведем через начало вектора   прямую b₁, параллельную прямой b, а через начало вектора  прямую a₁, праллельную прямой a. Плоскости, образуемые прямыми a и b₁, а так же прямымиb и a₁, параллельны по построению, а векторы   и   принадлежат им. Следовательно, векторы   и   компланарны.

Теорема.

Для компланарности трех векторов   и   трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Доказательство.

Пусть  , докажем что векторы   и   компланарны.

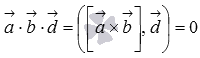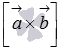Так как  , то векторы   и   перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор   перпендикулярен и вектору   и вектору  . Следовательно, векторы   и   компланарны, так как перпендикулярны одному вектору  .

Пусть теперь векторы   и   компланарны, докажем равенство нулю смешанного произведения  .

Так как векторы   и   компланарны, то вектор   перпендикулярен каждому из них, следовательно, скалярное произведение вектора   на   равно нулю, что означает равенство нулю смешанного произведения  .

Итак, теорема полностью доказана.

11)Дать опред. Уравнения на плоскости, вывести уравнение окружности данного радиуса с центром в данной точке.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

12) Вывести урав. Прямой по плоскости проход. Через данную точку проход. Перпендикулярно данному вектору.

Пусть дана точка М₀(x₀, y₀) и некоторый вектор N (A, B). Составим уравнение прямой линии, проходящей через данную точку и перпендикулярной заданному вектору. Для этого выберем произвольную точку М(x, y) на прямой. Тогда вектор

будет перпендикулярен вектору N (A, B). Записывая признак перпендикулярности векторов в координатной форме, получим A·( x - x₀ ) + B·( y - y₀ ) = 0.  Раскрывая скобки, получим общее уравнение прямой линии на плоскости

A·x + B·y + C = 0,

где С = − А·x₀ − B·y₀. Из этого уравнения виден смысл коэффициентов А и В – они являются координатами вектора, перпендикулярного прямой (являются координатами нормального вектора).

13)Написать общее уравнение прямой на плоскости, и исследовать частные случаи ее положения, когда один из коэф. уравнения =0; написать уравнение корд. осей.

Общее уравнение прямой линии на плоскости

 Линия, координаты точек которой удовлетворяют уравнению вида A·x + B·y + C = 0 является прямой линией на плоскости. Величины А, В и С являются параметрами линии.

14) Вывести уравнение прямой в отрезках

Выведем уравнение прямой линии, если известны точки пересечения прямой с осями координат А(а, 0) и В(0, b). Для этого воспользуемся уравнением прямой, проходящей через две точки

.

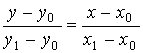В данном случае

Из этого уравнения легко получаем

— это и есть уравнение прямой в отрезках на осях: параметр b определяет точку пересечения прямой с осью OY, параметр а – с осью OX. Действительно, при x = 0 получаем y = b.

15) Вывести уравнение прямой на плоскости проход. через данную точку перпендикулярно данному вектору.

Определение. Прямая, проходящая через точку М₁ (х₁ , у₁ ) и перпендикулярная к прямой у = kx + b представляется уравнением:

16) Написать уравнение прямой заданным угловым коэф.

Уравнение прямой с угловым коэффициентом имеет вид  , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).

Давайте разберемся со смыслом фразы: «прямая на плоскости в фиксированной системе координат задана уравнением с угловым коэффициентом вида  ». Это означает, что уравнению   удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точкек плоскости. Таким образом, если при подстановке координат точки   в уравнение прямой с угловым коэффициентом  получается верное равенство, то прямая проходит через эту точку. В противном случае точка не лежит на прямой.

Пример.

Прямая задана уравнением с угловым коэффициентом  . Принадлежат ли точки   и   этой прямой?

Решение.

Подставим координаты точки   в исходное уравнение прямой с угловым коэффициентом:  . Мы получили верное равенство, следовательно, точка М₁ лежит на прямой.

При подстановке координат точки   получаем неверное равенство:  . Таким образом, точка М₂ не лежит на прямой.

Ответ:

точка М₁ принадлежит прямой, М₂ – не принадлежит.

Следует отметить, что прямая, определенная уравнением прямой с угловым коэффициентом  , проходит через точку  , так как при подстановке ее координат в уравнение мы получаем верное равенство:  .

Таким образом, уравнение прямой с угловым коэффициентом   определяет на плоскости прямую, проходящую через точку   и образующую угол   с положительным направлением оси абсцисс, причем  .

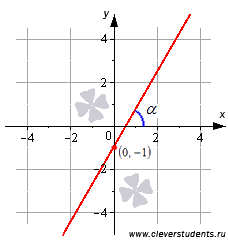
В качестве примера изобразим прямую, определяемую уравнением прямой с угловым коэффициентом вида  . Эта прямая проходит через точку   и имеет наклон   радиан (60 градусов) к положительному направлению оси Ox. Ее угловой коэффициент равен  .