5.5. Методы анализа основной тенденции (тренда) в рядах дина­мики

При анализе колебаний ряда динамики, при прогнозировании развития исследуемого явления на будущее возникает задача выявления основной его тенденции. Для решения по­добной задачи применяют методы:

• укрупнения интервалов;

• скользящих средних величин;

• аналитического выравнивания ряда динамики.

Метод укрупнение интервалов является одним из наиболее простых методов для изу­чения основной тенденции развития в рядах динамики. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количе­ство интервалов). Например, ряд ежесуточного выпуска продукции заменяется рядом месяч­ного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

Рассмотрим применение метода укрупнения интервалов на ежемесячных данных о выпуске продукции в сопоставимых ценах на предприятии в 2005 г.

Пример.

Имеются следующие данные.

Месяц	Объем производства, млн. руб.	Месяц	Объем производства, млн. руб.
Январь	15,1	Июль	15,6
Февраль	14,4	Август	13,9
Март	14,2	Сентябрь	16,1
Апрель	15,3	Октябрь	15,0
Май	13,6	Ноябрь	15,9
Июнь	15,8	Декабрь	16,2

Различные направления изменений уровней ряда по отдельным месяцам затрудняют получение выводов об основной тенденции производства.

Если соответствующие месячные уровни объединить в квартальные и вычислить ежемесячный выпуск продукции по кварталам, т.е. укрупнить интервалы, то решение задачи упрощается. Результаты расчетов представим в виде следующей таблицы:

Квартал	За квартал	В среднем за месяц
I	43,7	14,57
II	44,7	14,90
III	45,6	15,20
IV	47,1	15,70

После укрупнения интервалов основная тенденция роста производства стала очевид­ной: 14,57 < 14,90 < 15,20 < 15,70 млн. руб.

Метод скользящих средних величин . Его суть состоит в том, что исчисляется средний уровень из определенного числа (нечетного или же четного), первых по счету фактических уровней ряда, затем - из такого же числа уровней, но начиная со второго по счету, далее - начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, пере­двигаясь на один временной срок.

Недостатком сглаживания ряда с помощью скользящих средних величин является «укорачивание» сглаженного ряда по сравнению с фактическим, а, следовательно, потеря информации.

Расчеты, необходимые для сглаживания ряда динамики с помощью трехчленной и че­тырехчленной скользящих средних величин приведены в таблице.

Пример

Рассмотрим ряд, характеризующий производство мобильных телефонов N-ой фирмой за 15 месяцев.

Меся­	Производ­	Трехчленные	Трехчленные	Четырехчленные	Четырехчлен-	Четырехчлен-
цы	ство мо­	скользящие	скользящие	скользящие сум-	ные скользя-	ные скользя-
	бильных те­	суммы	средние	мы	щие средние	щие средние
	лефонов,				(нецентриро-	(нецентриро-
	тыс. шт.				ванные)	ванные)
1	155	-	-	-		-
2	163	-	485/3=161,7	-		-
					616/2=154,0
3	167	155 + 163 +	461/3=153,7	-		(154,0+154,8)/2
		167 = 485				= 154,4
					619/4=154,8
4	131	163 + 167 +131	152,0	155 + 163 + 167 +		(154,8+150,8)/2
		= 461		131=616		= 152,8
					150,8
5	158	456	145,3	163 + 167 + 131 +		146,2
				158 = 619
					141,5
6	147	436	145,0	603		143,3
					145,0
7	130	435	140,7	566		141,3
					137,5
8	145	422	134,3	580		136,7
					135,8
9	128	403	137,7	550		139,4
					143,0
10	140	413	142,3	543		144,9
					146,8
11	159	427	153,0	572		149,2
					151,5
12	160	459	155,3	587		152,8
					154,0
13	147	466	152,3	606		154,8
					155,5
14	150	457	154,0	616		-
15	165	462	-	622		-

Рассмотренные приемы сглаживания динамических рядов дают возможность опреде­лить лишь общую тенденцию развития явления, более или менее освобожденную от случай­ных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.

Аналитическое выравнивание ряда динамики

Для того чтобы дать количественную модель, выражающую основную тенденцию из­менения уровней динамического ряда во времени, используется аналитическое выравнива­ние ряда динамики.

Основным содержанием метода аналитического выравнивания в рядах динамики яв­ляется то, что общая тенденция развития рассчитывается как функция времени

у< = у(<),

где у_< - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней у_г, производится на основе так

называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теорети­ческом анализе, выявляющем характер развития явления, а также на визуальном анализе графического изображения ряда динамики (линейной диаграммы).

Например, простейшими моделями (формулами), выражающими тенденцию развития, являются:

• линейная функция - прямая y_t = ao + ait,

• показательная функция y_t = a₀ a₁,

• степенная функция - кривая второго порядка (парабола) y_t = a₀ + a₁t + a₁t .

Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями:

X⁽у ^- y_t ⁾² ^ mi^

где y_t - выравненные (расчетные) уровни; у - фактические уровни.

Параметры уравнения a_i, удовлетворяющие этому условию, могут быть найдены ре­шением системы нормальных уравнений. На основе найденного уравнения тренда вычисля­ются выравненные уровни. Таким образом, выравнивание ряда динамики заключается в за­мене фактических уровней (у ), плавно изменяющимися уровнями (y_t), наилучшим образом

аппроксимирующими статистические данные.

Система нормальных уравнений для аналитической выравнивающей прямой и ее ре­шение (в случае переобозначения показателей времени таким образом, чтобы Е t = 0) имеют следующий вид:

[X у=nao

\X yt = aX t²;.

^ (5.21.)

=X у =Xz!

^a0 ^{, a}1 ^ 2 п X^t

Рассмотрим реализацию метода аналитического выравнивания ряда динамики, харак­теризующего производство мобильных телефонов по аналитической линии - параболе.

Упрощенная система нормальных уравнений (в случае переобозначения показателей времени таким образом, чтобы X t = 0) для аналитической параболы выглядит следующим образом:

X у = ^na0 + ^a2 X^t ^ X yt = a X t², (5.22.)

X у^{: 2} = a0 X¹² + a2 X¹⁴-

Необходимые расчеты для составления системы нормальных уравнений разместим в таблице.

	Производство мобильных
Месяцы	телефонов, тыс. шт. у	t	t2	t4	у • t	у • t2	у:
1	155	-7	49	2401	-1085	7595	163,15
2	163	-6	36	1296	-978	5868	157,41
3	167	-5	25	625	-835	4175	152,55
4	131	-4	16	256	-524	2096	148,57
5	158	-3	9	81	-474	1422	145,47
6	147	-2	4	16	-294	588	143,25
7	130	-1	1	1	-130	130	141,91
8	145	0	0	0	0	0	141,45

9	128	1	1	1	128	128	141,87
10	140	2	4	16	280	560	143,17
11	159	3	9	81	477	1431	145,35
12	160	4	16	256	640	2560	148,41
13	147	5	25	625	735	3675	152,35
14	150	6	36	1296	900	5400	157,17
15	165	7	49	2401	1155	8085	162,87
Итого	2245	0	280	9352	-5	43713

Следовательно, система нормальных уравнений будет иметь следующее решение: а₀ = 141,45; ах = - 0,02; а2 = 0,44.

Уравнение параболы можно использовать для получения прогнозный значений произ­водства мобильнык телефонов в следующих месяцах.

Например, для 16-го месяца t = 8 и y_t = 141,45 - 0,02*8 + 0,44*8² = 169,45 тыс. шт., а для 17-го месяца t = 9 и y_t = 141,45 - 0,02*9 + 0,44*9² = 176,91 тыс. шт.

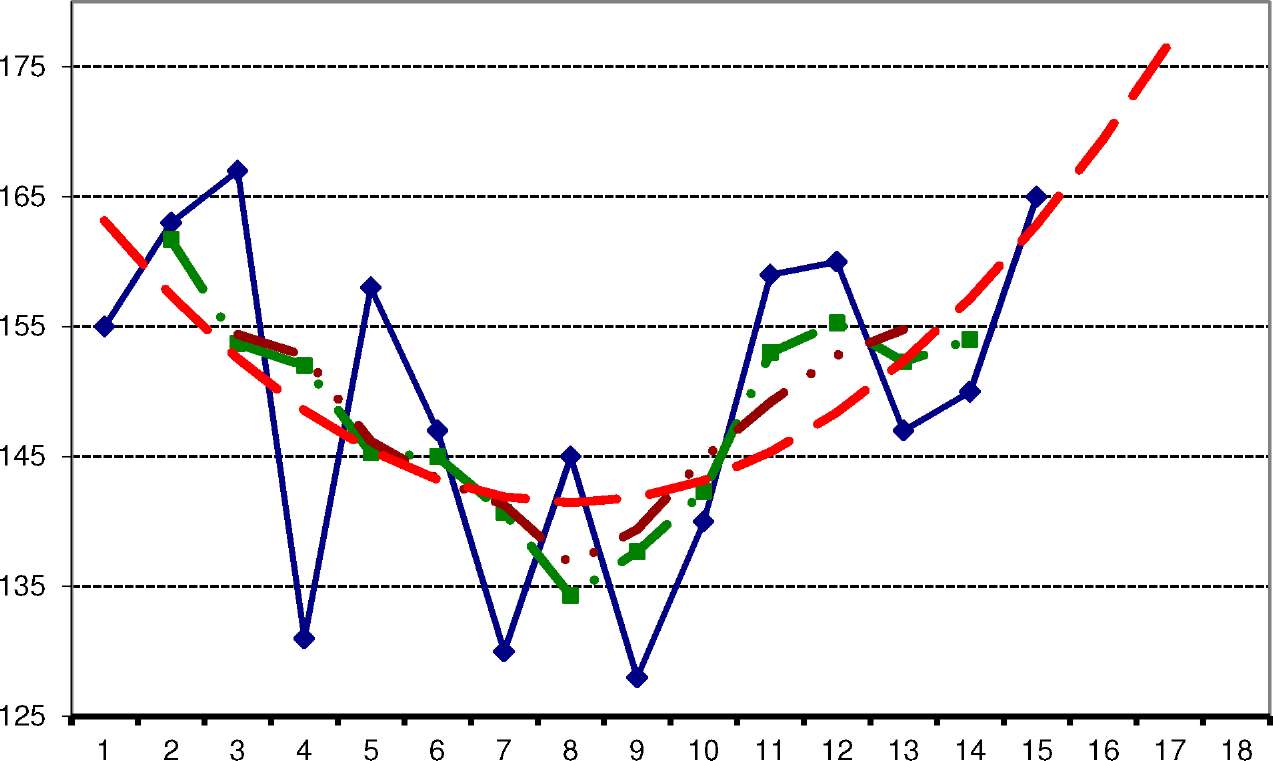
Фактические и расчетные значения (полученные на основании применения методов сглаживания с помощью скользящих средних величин и аналитического выравнивания) про­изводства мобильнык телефонов представлены в виде графиков в одной системе координат (рисунок 5.1.).

• фактические данные ^^^ 3-х членные скользящие средние

4-х членные скользящие средние аналитическая парабола

Рисунок 5.1. Фактические и расчетные значения производства мобильных телефонов

за 15 месяцев