3. Понятие вариации

Термин «вариация» произошел от латинского variation - изменение, колеблемость, различие. Однако не всякие различия принято называть вариациеИ.

Под вариациеИ в статистике понимают количественные изменения величины исследу­емого признака у разных единиц в пределах изучаемоИ совокупности, в один и тот же пе­риод или момент времени.

В отличие от вариации различия значениИ признака у одного и того же объекта, у од- ноИ и тоИ же единицы совокупности в разные моменты или периоды времени следует назы­вать изменениями во времени и колебаниями. Методы их измерения и изучения отличаются принципиально от методов измерения вариации

Различают случаИную и систематическую вариацию признака. Анализ систематиче- скоИ вариации позволяет оценить зависимости изменениИ в изучаемом признаке от опреде­ляющих ее факторов. Например, изучая силу и характер вариации в выделенноИ совокупно­сти, можно оценить, насколько однородноИ является данная совокупность в количественном, а иногда и в качественном отношении, а следовательно, насколько характерноИ является ис­численная средняя величина.

ПричиноИ вариации являются разные условия существования разных единиц сово­купности. Даже однояИцовые близнецы в процессе своего развития приобретают различия в росте, весе, не говоря уже о таких признаках, как специальность, образование, заработная плата (доход), число детеИ и т.д. Еще больше причин влияют на различия промышленных предприятиИ, магазинов и т.д.

Вариация присуща всем без исключения явлениям природы и общества, кроме зако­нодательно закрепленных нормативных значениИ отдельных социальных признаков: не ва­рьирует признак "число глав муниципальных образованиИ" - все они имеют по одноИ главе.

Не варьирующие признаки не представляют интереса для статистики; предметом изу­чения статистики является вариация. Большинство методов статистики - это либо методы измерения вариации, либо методы абстрагирования от нее.

Итак, в жизни общества, как и в природе, каждоИ массовоИ совокупности, массовому процессу присуща некоторая специфическая мера вариации ее элементов, при котороИ дан- ныИ процесс протекает оптимально.

Чтобы руководитель предприятия, менеджер, могли управлять вариациеИ и изучать ее, статистикоИ разработаны специальные методы исследования вариации, система показате- леИ, с помощью котороИ вариация измеряется, характеризуются ее своИства.

3. Методы анализа вариации

Основное значение средних величин состоит в их обобщающеИ функции, т.е. в замене множества различных индивидуальных значениИ признака среднеИ величиноИ, характеризу- ющеИ всю совокупность явлениИ. Средняя величина отражает наиболее характерныИ и часто встречающиИся уровень признака. Но при одинаковоИ среднеИ величине совокупности могут различаться характером вариации значениИ признака у отдельных единиц совокупности, и если разброс индивидуальных значениИ вокруг среднеИ становится слишком значительным, то средняя величина теряет свою типичность и становится фиктивноИ. Для оценки степени варьирования количественных признаков используют пять показателеИ:

• размах вариации;

• среднее линеИное отклонение;

• дисперсию;

• среднее квадратическое отклонение;

• коэффициент вариации.

Размах вариации означает разность максимального и минимального значениИ призна­ка ^R = ^X_max ^{- X}min .

Он характеризует амплитуду колебаниИ вариантов, но учитывает только два экстре­мальных значения и не отражает вариации всех остальных значениИ.Среднее линейное отклонение рассчитывается, чтобы учесть вариацию всех значений:

d = £ |х - * ■ f / £ f (4.6.)

Все отклонения необходимо взять с положительным знаком, по абсолютной величине, иначе сумма всех отклонений от средней величины всегда будет равняться нулю. Измеряется линейное отклонение в тех же единицах, что и сам признак.

Третьим показателем является дисперсия, или средний квадрат отклонений. Все от­клонения возводим в квадрат и из этих полученных положительных значений находим сред­нее:

а² = £ (х - X)² ■ f / £ f (4.7.)

Единицы измерения дисперсия не имеет.

Среднее квадратическое отклонение вычисляется как корень квадратный из диспер­сии:

а = V£ (х - X)² ■ f / £ f (4.8.)

Оно является абсолютной мерой вариации, измеряется в тех же единицах, что и сам признак, и поэтому позволяет сравнивать вариацию только одноименных признаков в раз­личных совокупностях. При существенных различиях в средней величине в динамике или между совокупностями применение среднего квадратического отклонения невозможно.

Коэффициент вариации является наиболее точным показателем, который позволяет также сравнивать вариацию разноименных признаков. Он рассчитывается как процентное отношение среднего квадратического отклонения к средней величине этого признака:

v = a / X ■ 100 (4.9.)

Если коэффициент вариации превышает 30 %, то средняя величина становится фик­тивной, т.е. изучаемая совокупность не является количественно однородной, в ней суще­ствуют отдельные типичные группы с очень низким и очень высоким значениями изучаемо­го признака, что требует вычисления средних величин отдельно по этим типичным группам.

В статистических исследованиях наиболее широко применяется дисперсия, которая имеет важные математические свойства, позволяющие рассчитывать ее сокращенным мето­дом - методом отсчета от условного нуля, или методом моментов.

1. Если из всех значений признака выгчестъ постоянное число, то дисперсия от этого не изменится. При уменъшении значений признака на постоянное число средняя также уменъшается на это же число, а размер отклонений индивидуалъныгх значений от средней остается прежним, следователъно, дисперсия как характеристика величиныг отклонений сохраняется.

2. Если все значения признака разделитъ на постоянное число, то среднее квадрати­ческое отклонение уменъшится во столъко же раз, а дисперсия уменъшится на величину квадрата этого числа.

3. Дисперсия, выгчисленная от средней величиныг, обладает свойством минималъно- сти, т.е. она менъше дисперсий, выгчисленныгх от любыгх других величин А, причем менъше на квадрат разности между этими величинами и средней величиной:

а\ =а* + (х - А)²,

отсюда

а\ =а²_х + (х - А)²,

2

где а а - средний квадрат отклонений от произвольной величины А;

2 „ — а_х - дисперсия от средней х .

Если А приравниваем к нулю, получим вторую формулу вычисления дисперсии от средней величины, которой широко пользуются на практике:

а² = £х² f /£ f - (£-f /£ f )² (4.10.)

<² — (x% - (х)²

Следовательно, средний квадрат отклонений равен среднему квадрату признака минус квадрат среднего значения признака.

На использовании трех важнейших свойств дисперсии основан сокращенный метод ее вычисления - метод моментов. Дисперсия, рассчитанная методом моментов, равна квадрату величины интервала, умноженному на разность момента второго порядка и квадрата момен­та первого порядка:

2

ных

2 2 2 7 — i (m₂ - m₁ )

Более подробная запись имеет вид

7² — i² £ x'² f / £ f - (£xf / £ f)

где i - величина интервала.

Момент первого порядка (m1 — £ x f / £ f) - это средняя величина из сокращен- значений, т. е. из натурального ряда чисел. Момент второго порядка (m2 — £ x'² f / £ f) - это средняя из квадратов тех же сокращенных значений.

Расчет дисперсии методом моментов рассмотрим на следующем примере. Имеются данные о выборочной проверке качества ламп общего назначения по времени горения. Необ­ходимо рассчитать показатели вариации времени горения. Расчет проведем с помощью ме­тода моментов (табл. 2.1).

Таблица 2.1.

Распределение ламп по времени горения Время горения лампы, ч	Количество ламп, шт.	Расчетные значения
		x	х'	х f	(x У	( x' )2 f
До 800	30		775	-3	-90	9	270
800-850	130		825	-2	-260	4	520
850-900	150		875	-1	-150	1	150
900-950	250		925	0	0	0	0
950-1000	160		975	1	160	1	160
Свыше 1000	80		1025	2	160	4	320
Итого	800				-180		1420

Прежде всего перейдем к серединам интервалов, а затем сократим исходные значения до натурального ряда чисел по формуле х' = х - A/i, вычитая из всех значений А = 925 и раз­делив на i = 50.

Рассчитаем момент первого порядка:

m — x' — £ x f /£ f —-180/800 — -0,225

затем определим момент второго порядка:

m₂ — x'² — £x ² f /£ f —1420/800 —1,775

Вычислим дисперсию

7² — i²(m₂ - m²) — 50² [1,775 - (-0,225)²]— 4310,9

Среднее время горения также определим методом моментов:

х — х' • i + А — -0,225 • 50 + 925 — 913,75ч. Расчет дисперсии по основной формуле будет иметь следующий вид:

(775 - 913,25)² • 30 + (825 - 913,25)² • 130 +

2 £(x-x)² f + (875-913,25)² 150 + (925-913,25)² • 80 3448720 .._Л1._п

а = = = = 4310,9

£ f 30 +130 +150 + 250 + +160 + 80 800

При сопоставлении вычислений видно, что объем вычислительной работы по методу моментов в десятки раз меньше и, соответственно, вероятность ошибок в расчете также уменьшается.

В этом случае среднее квадратическое отклонение имеет вид

а = 74310,9 = 65,66 ч.

Это число означает, что при среднем времени горения электроламп в 913,25 ч откло­нения индивидуальных значений в среднем составляет 65,66 ч в большую или меньшую сто­рону.

Коэффициент вариации вычисляется как

v = a/ x • 100 = 65,55/913,25 • 100 = 7,2%

Данное значение характеризует высокую однородность совокупности по времени го­рения и типичность вычисленного среднего значения.

Размах вариации в этом примере определим как разность возможного максимального и возможного минимального значений:

1050 - 750 = 300 ч.

Если изучаемая совокупность разбита на группы по какому-либо факторному призна­ку (х), то для результативного признака (у) могут быть вычислены следующие виды диспер­сии:

1. Общая дисперсия имеет вид

а² = £ (у - у)² • f /£ f (4.11.)

Она характеризует вариацию результативного признака за счет всех факторов и при­чин, действующих в изучаемой совокупности.

2. Внутригрупповые дисперсии результативного признака рассчитываются по форму­ле

а² = £ (у, - у, )² • f / £ f (4.12.)

Они характеризуют вариации результативного признака внутри каждой группы во­круг среднего значения для этой группы у, Вариации, или различия индивидуальных значе­ний, обусловлены действием всех факторов вместе, за исключением группировочного, в от­ношении которого все единицы в группе однородны. Такие дисперсии рассчитывают по ко­личеству образованных групп.

3. Средняя из внутригрупповых дисперсий рассчитывается по формуле

а,² = £а,² • f / £ f (4.13.)

Она находится из групповых дисперсий взвешиванием значений по численности каж­дой группы. Эта дисперсия означает характеристику степени влияния на результативный признак всех факторов вместе, кроме группировочного.

4. Межгрупповая дисперсия

= £ (у, - у)² • f / £ f (4.14.)

Характеризует вариацию, или различия групповых средних от общей средней. Эти различия обусловлены действием только одного группировочного фактора. Чем сильнее он влияет на результативный признак, тем больше групповые средние результативного призна­ка (у,), отличаются от общего среднего значения (у ), тем значительнее величина межгруп­повой дисперсии.

Таким образом, общая вариация результативного признака, связанная с действием всех факторов и причин, разделяется на две части: первая связана с действием только груп- пировочного фактора и выражается межгрупповой дисперсией, вторая обусловлена действи­

ем всех остальных факторов, кроме группировочного, и выражается среднеИ из внутригруп- повых дисперсиИ.

По правилу сложения дисперсиИ общая дисперсия равна сумме среднеИ из внутриг- рупповых и межгрупповоИ дисперсии:

а² =а2 +S² (4.15.)

На этом соотношении основывается вычисление основных показателеИ степени взаи­мосвязи факторных и результативных признаков в дисперсионном анализе: коэффициента детерминации и эмпирического корреляционного отношения.

Эмпирическое корреляционное отношение показывает тесноту связи между результа­тивным и факторным признаком. Оно рассчитывается как квадратныИ корень из коэффици­ента детерминации и изменяется в пределах от нуля до единицы.

Коэффициент детерминации показывает долю вариации результативного признака обусловленную вариациеИ факторного признака. Чем сильнее влияние факторного признака, тем больше межгрупповая дисперсия и больше ее удельныИ вес в общеИ дисперсии. (Если коэффициент детерминации равен 0,7, то 70% вариации результативного признака объясня­ется влиянием одного факторного признака, а остальные 30% вариации связаны с деИствием всех остальных факторов и причин вместе взятых).

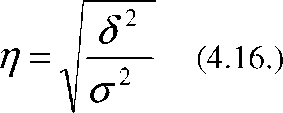
(4.15.)

ДанныИ показатель принимает значения от 0 до 1. Чем ближе к 1 будет его величина, тем теснеИ взаимосвязь.

Нулевое значение получим в том случае, когда межгрупповая дисперсия будет равна нулю, а это происходит при равенстве групповых средних и общеИ среднеИ. В этом случае отсутствует какое-либо влияние факторного признака на результативныИ.

Значение единица может быть получено при равенстве межгрупповоИ и общеИ дис­персии, в этом случае остаточная дисперсия будет равна нулю и взаимосвязь из корреляци- онноИ многофакторноИ, превращается в функциональную между факторным и результатив­ным показателями, чего в анализе экономических явлениИ не встречается.

Для характеристики тесноты взаимосвязи между признаками по значениям эмпириче­ского корреляционного отношения применяется следующая шкала: до 0,3 - слабая взаимосвязь признаков, или ее отсутствие

от 0,3 до 0,6 - средняя степень взаимосвязи, фактор является важным, но не решаю­щим

от 0,6 до 0,8 - сильная степень взаимосвязи, группировочныИ фактор является глав­ным или основным по воздеИствию на результативныИ признак

свыше 0,8 - очень сильная степень и взаимосвязь между факторным и результатив­ным признаками приближается к функциональной

На основе последовательноИ группировки по различным факторным признакам полу­чаем значения эмпирического корреляционного отношения, которые позволят провести ран­жирование факторных признаков по степени их влияния на результативныИ признак и выде­лить наиболее значимые. Это позволит наметить первоочередные направления воздеИствия на результативныИ показатель.

Наряду с вариациеИ количественных признаков необходимо изучать вариацию каче­ственных признаков, которые отличаются у отдельных единиц совокупности не величиноИ, а какими-либо существенными своИствами, например, профессиеИ (для категории работаю­щих). Если качественныИ признак может принимать только одно из двух противоположных значениИ, он называется альтернативным. Вариацию количественных признаков можно условно представить как альтернативную. Образуем, например, две группы: одна включает рабочих со стажем до 10 лет, вторая - свыше 10 лет. Таким образом, можно оценить вариа­

цию стажа работы в различных группах как вариацию альтернативного признака, имеющего только два противоположных значения.

Мерой вариации альтернативного признака служит дисперсия

а² = а(1 -а) (4.17.) где С - доля единиц в совокупности, обладающих одним из двух противоположных значений альтернативного признака.