2. Ортонормированный базис и скалярное произведение в нём

В ортонормированном базисе евклидова пространства скалярное произведение приобретает особенно простой вид, а именно имеет место следующая теорема.

Теорема. В ортонормированном и только в ортонормированном базисе евклидова пространства скалярное произведение произвольной пары векторов и равно:

,

где − координаты вектора и − координаты вектора .

Доказательство. Пусть − ортонормированный базис пространства и , 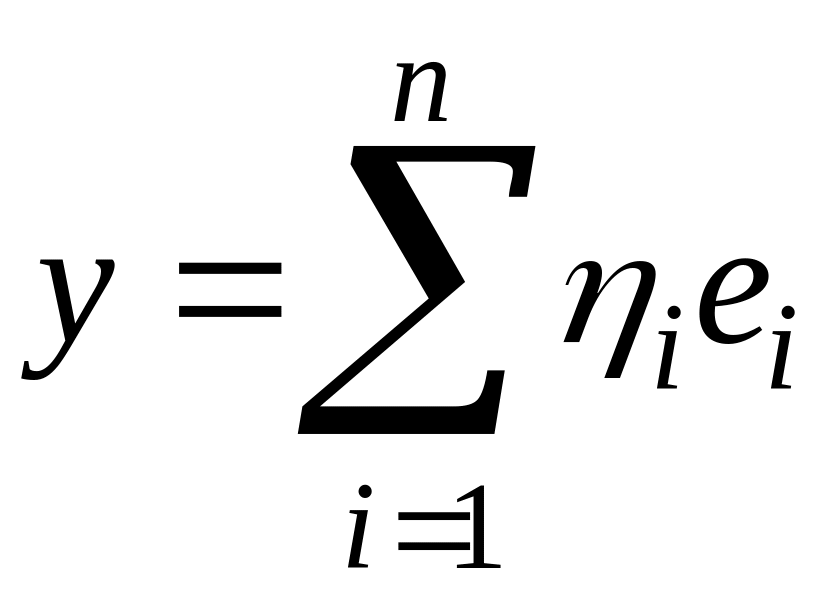− произвольная пара векторов. Тогда

, .

Но и при . Следовательно,

. (*)

Обратно, пусть скалярное произведение произвольной пары векторов , выражается в некотором базисе формулой (3). Так как вектор имеет -ю координату, равную 1, а остальные его координаты равны пулю, то по формуле (*) получается, что . Аналогично по той же формуле получается при , что . Мы видим отсюда, что − ортонормированный базис.

2. Изоморфизм евклидовых пространств

Введем понятие изоморфизма евклидовых пространств. Пусть и − два каких-нибудь евклидова пространства. Назовем их изоморфными, если:

1) они изоморфны как аффинные пространства, т. е. как линейные пространства, в которых не определено скалярное произведение;

2) изоморфное отображение сохраняет скалярное произведение: , где , − векторы из и , − их образы из .

Назовем, далее, действительное пространство -мерных строк (и аналогично действительное пространство -мерных столбцов) евклидовым, если в этом пространстве скалярное произведение любой пары строк и равно . Евклидово пространство -мерных строк мы будем обозначать через (и через − евклидово пространство -мерных столбцов).

Отсюда видно, что строки образуют ортонормированный базис пространства .

Оказывается, что всякое -мерное евклидово пространство можно рассматривать с точностью до изоморфизма как евклидово пространство -мерных строк, а именно справедлива следующая теорема.

Теорема. Евклидово пространство изоморфно евклидову пространству ( ).

Доказательство. Возьмем какой-нибудь ортонормированный базис пространства и каждому вектору из поставим в соответствие его координатную строку . Рассуждаем так же, как и при доказательстве теоремы 2 для линейных пространств, приходим к выводу, что пространства и изоморфны в аффинном смысле. Возьмем еще один вектор из . Образом вектора будет его координатная строка . При ортонормированном базисе скалярное произведение векторов и пространства должно быть равно . Но согласно определению евклидова пространства скалярное произведение строк и равно тому же числу . Мы видим, что , и теорема доказана.

Из теоремы вытекает в силу симметрии и транзитивности изоморфного отображения, что всякие два евклидова пространства одинаковой размерности изоморфны. Если же размерности двух евклидовых пространств различны, то они уже в аффинном смысле не могут быть изоморфными.

2. Ортогональное преобразование

Уже в аналитической геометрии на плоскости приходится встречаться с поворотом направленных отрезков, исходящих из начала прямоугольной системы, на один и тот же угол вокруг начала и с отражением, т. е. изменением направления всех таких отрезков. Характерной особенностью этих преобразований является то, что они оставляют неизменным длину направленного отрезка. Здесь мы рассмотрим более общее понятие, а именно ортогональное преобразование евклидова пространства.

Линейное преобразование евклидова пространства называется ортогональным, если оно не изменяет скалярный квадрат любого вектора : .

Теорема 1. Линейное преобразование евклидова пространства ортогонально тогда и только тогда, когда оно не изменяет скалярное произведение любой пары векторов , : .

Таким образом, ортогональное преобразование можно определить как такое линейное преобразование пространства , которое оставляет неизменным скалярное произведение .

Доказательство. Если линейное преобразование не изменяет скалярное произведение , то, полагая в равенстве вектор равным вектору , получаем: , т. е. − ортогональное преобразование.

Обратно, если − ортогональное преобразование, то

.

Но

,

так как , и

так как , и

.Следовательно,

,

откуда , т. е. преобразование не изменяет скалярное произведение .

Ортогональное преобразование можно определить иначе. А именно:

Теорема 2. Ортогональное преобразование переводит ортонормированный базис евклидова пространства в ортонормированный базис. Обратно, линейное преобразование пространства , переводящее ортонормированный базис в ортонормированный базис, является ортогональным.

Доказательство. Пусть − ортонормированный базис , и преобразование ортогонально. Рассмотрим систему образов векторов базиса. Так как − ортонормированный базис, то в силу ортогональности

,

при .

Мы видим, что − ортонормированная (и тем самым линейно независимая) система векторов, т. е. ортонормированный базис.

Обратно, пусть − линейное преобразование пространства , для которого система образов векторов ортонормированного базиса также является ортонормированным базисом: , при , .

Возьмем произвольный вектор . Так как − ортонормированный базис, то . Образ вектора равен:

.

Отсюда в ортонормированном базисе

,

и мы видим, что ), т.е. − ортогональное преобразование.