ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

Федеральное бюджетное образовательное учреждение

высшего профессионального образования

«Санкт-Петербургский Государственный университет

водных коммуникаций»

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

Т.А. Волкова, Т.П. Кныш

ЕВКЛИДОВО ПРОСТРАНСТВО

И КВАДРАТИЧНЫЕ ФОРМЫ

Санкт-Петербург

2012

УДК 512.64

ББК 22.143

Рецензент: кандидат технических наук, доцент Шкадова А.Р.

Т.А. Волкова, Т.П. Кныш.

Евклидово пространство и квадратичные формы: конспект лекций. – СПб.: СПГУВК, 2012 – с.

Конспект лекций предназначен для студентов второго курса направления бакалавриата 010400.62 «Прикладная математика и информатика» и первого курса направления бакалавриата 090900.62 «Информационная безопасность».

Пособие содержит полный конспект лекций по одному из разделов дисциплины «Геометрия и алгебра» для направления 010400.62 и дисциплине «Алгебра и геометрия» для направления 090900.62 Учебное пособие соответствует рабочим программам дисциплин, стандартам указанных специальностей и может быть использовано при подготовке к экзамену студентами и преподавателями.

УДК 512.64

ББК 22.143

©Санкт-Петербургский государственный

университет водных коммуникаций, 2012

Евклидово пространство

1. Определение и примеры Евклидовых пространств

Многие свойства объектов, встречающихся в геометрии, тесно связаны с возможностью измерения длин отрезков и угла между прямыми. В линейном пространстве мы еще не можем производить такие измерения, вследствие чего область применения общей теории линейных пространств к геометрии и к ряду других математических дисциплин довольно сильно сужается. Это затруднение, однако, может быть устранено, если ввести понятие скалярного произведения двух векторов. А именно, пусть − линейное -мерное действительное пространство. Поставим в соответствие каждой паре векторов , действительное число и назовем это число скалярным произведением векторов и , если удовлетворяются следующие требования:

1. (коммутативный закон).

2. , .

3. для любого действительного .

4. для любого ненулевого вектора .

Скалярное произведение является частным случаем понятия числовой функции двух векторных аргументов, т. е. функции, значения которой суть числа. Мы можем, следовательно, назвать скалярным произведением такую числовую функцию векторных аргументов , , значения которой действительны для любых значений аргументов из и для которой удовлетворяются требования 1 − 4.

Действительное линейное пространство , в котором определено скалярное произведение, будет называться евклидовым и будет обозначаться через .

Отметим, что в евклидовом пространстве скалярное произведение нулевого вектора на любой вектор равно нулю: . Действительно, , и в силу требования 3 . Полагая , получаем, что . Отсюда, в частности, .

Примеры.

1. Пусть − обычное трехмерное пространство геометрических векторов с общим началом в точке . В аналитической геометрии скалярным произведением двух таких векторов называется действительное число, равное , где и − длины векторов и , а − угол между векторами , , и доказывается, что для этого числа удовлетворяются все требования 1 − 4.

Таким образом, введенное нами понятие скалярного произведения является обобщением понятия скалярного произведения геометрических векторов.

2. Рассмотрим пространство 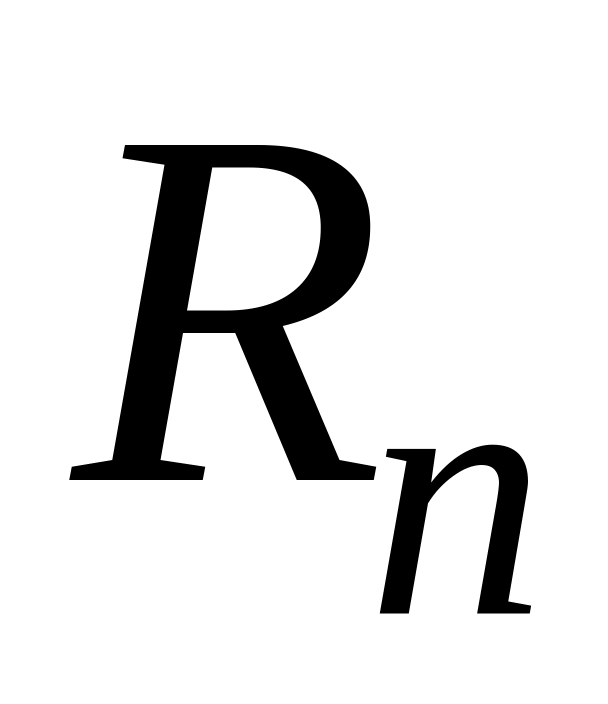– мерных строк с действительными координатами и поставим в соответствие каждой паре и таких векторов-строк действительное число

Легко проверить, что для этого числа удовлетворяются все требования 1 − 4:

для и .

и аналогично . Далее,

,

и аналогично . Наконец,

, при ,

так как по меньшей мере одно из чисел при отлично от нуля.

Мы видим отсюда, что это число является скалярным произведением векторов строк и , а пространство , после того как мы ввели такое скалярное произведение, становится евклидовым.

3. Пусть — линейное действительное -мерное пространство и − некоторый его базис. Поставим в соответствие каждой паре векторов , действительное число . Тогда пространство превратится в евклидово, т. е. число будет скалярным произведением векторов и . В самом деле:

,

где

, .

Затем

и

.

.

Наконец,

при

Можно даже другими способами превратить наше пространство в евклидово, например, мы могли бы поставить в соответствие паре векторов , действительное число

и легко проверить, что для такого числа удовлетворяются все требования 1 − 4, характеризующие скалярное произведение. Но так как здесь (при том же базисе ) мы определили другую числовую функцию , то из получается другое евклидово пространство с другим «мероопределением».

4. Наконец, обращаясь к тому же пространству , рассмотрим числовую функцию , которая при , определяется равенством . Эта функция уже не является скалярным произведением, так как нарушается требование 4: при , вектор равен , a . Тем самым здесь из не получается евклидова пространства.

Пользуясь требованиями 2 и 3, входящими в определение скалярного произведения, легко получить следующую формулу:

,

где , − две произвольные системы векторов. Отсюда, в частности, получается при произвольном базисе и для любой пары векторов , , что

, (1)

где . Выражение в правой части равенства (1) есть многочлен от и и называется билинейной формой от и (каждый ее член является линейным, т.е. первой степени, как относительно , так и относительно ). Билинейная форма называется симметрической, если для каждого ее коэффициента выполняется условие симметрии . Таким образом, скалярное произведение в произвольном базисе выражается в виде билинейной симметрической формы от координат векторов , с действительными коэффициентами. Но этого еще недостаточно. А именно, полагая , получаем из равенства (1), что

, (2)

Выражение в правой части равенства (2) есть многочлен от координат вектора и называется квадратичной формой от (степень каждого его члена равна двум). Квадратичная форма с действительными коэффициентами называется положительно определенной, если она принимает строго положительное значение при всяком ненулевом наборе действительных значений неизвестных . Таким образом, в силу требования 4 скалярный квадрат в произвольном базисе выражается в виде положительно определенной квадратичной формы от .

Можно убедиться, что, обратно, всякая билинейная симметрическая форма с действительными коэффициентами от координат и векторов и в некотором базисе определяет скалярное произведение, если при эта билинейная форма превращается в положительно определенную квадратичную форму.

Итак, в зависимости от выбранного базиса получается для скалярного произведения та или иная формула. Возникает вопрос: нельзя ли указать такой базис, при котором скалярное произведение имело бы наиболее простое выражение? Чтобы ответить на этот вопрос, введем несколько новых понятий.