31. Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.А).
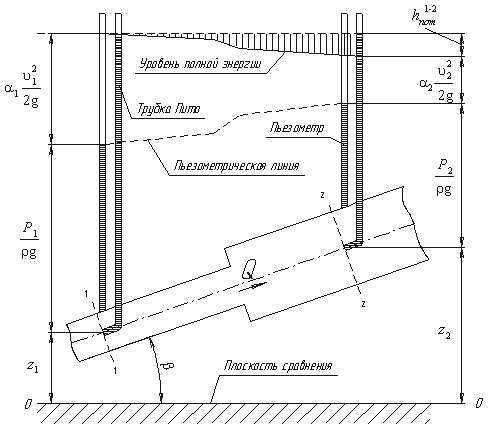
Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность. Из рис.А видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2. Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ). Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока) С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ1ω 1 = υ2ω2.
32. Дифференциальные уравнения движущейся идеальной жидкости(уравнение л. Эйлера). Вывод уравнений.
Способ Эйлера. В этом способе движение жидкости описывается функциями, выражающими изменения скоростей в точках некоторой неподвижной области, выбранной в пределах потока. В данный момент времени в каждой точке этой области, определяемой координатами х, у, z, находится частица жидкости, имеющая некоторую скорость u.
Эта скорость называется мгновенной местной скоростью. Совокупность мгновенных местных скоростей представляет векторное поле, называемое полем скоростей. В общем случае поле скоростей может изменяться во времени и по координатам:
-
Это уравнения Эйлера
Рассмотрим
установившееся движение жидкости:
-
если учесть, что:
,
то получим:
или
,
где U-силовая
функция.
Интегрирование этого уравнения выполним для основного частного случая, когда на жидкость действует лишь одна массовая сила- сила тяжести. При направлении оси z вертикально вверх: X=0 , Y=0, Z=-g.
Подставив
эти значения получим:
или
Так
как для несжимаемой жидкости
предыдущее уравнение можно переписать
в виде:
.
Следовательно указанный трёхчлен есть
величина постоянная вдоль линии тока,
а значит и вдоль элементарной струйки,
т.е.
33.
Так как размер отверстия предполагается малым по сравнению с напором Н0 и размерами резервуара, и следовательно, его боковые стенки и свободная поверхность жидкости не влияют на приток жидкости к отверстию, то наблюдается совершенное сжатие струи.
Степень сжатия оценивается коэффициентом сжатия ε, равным отношению площади сжатого поперечного сечения струи к площади отверстия:
;
Скорость истечения:
;
где ϕ – коэффициент скорости:
;
;
Произведение коэффициентов ε и ϕ принято обозначать буквой µ и называть коэффициентом расхода:
;
Из этого следует, что расход жидкости равен:
или
.
– уравнение
Торичелли (скорость истечения идеальной
жидкости).
34.
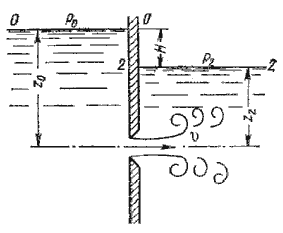
Если жидкость истекает не в атмосферу, а в пространство, заполненное этой же жидкостью, то такой случай называется истечением под уровень, или истечением через затопленное отверстие.
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
Где φ – коэффициент скорости; Н - расчетный напор,
.
Р
асход
жидкости равен
Таким образом, имеем те же расчетные формулы, что и при истечении в атмосферу, только напор Н в данном случае представляет собой разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.
35.
Запишем уравнение для определения объема, вытекающего из резервуара за промежуток времени dt:
;
или
;
Знак минус обусловлен тем, что положительному приращению dt соответствует отрицательное приращение dh.
Отсюда время полного опорожнения сосуда высотой Н:
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const, следовательно, время его полного опорожнения:
.
37.
Насадок – это короткий трубопровод, непосредственно подсоединённый к сосуду с жидкостью. Насадок улучшает условия вытекания жидкости.
Насадок Вентури:
Скорость истечения жидкости:
;
Величина расхода:
.
Насадок Борда:
Скорость истечения жидкости:
Сходящийся насадок:
Расходящийся насадок:
Скорость истечения жидкости:
;
Величина расхода:
;
38.
Так как размер отверстия предполагается малым по сравнению с напором Н0 и размерами резервуара, и следовательно, его боковые стенки и свободная поверхность жидкости не влияют на приток жидкости к отверстию, то наблюдается совершенное сжатие струи.
Степень сжатия оценивается коэффициентом сжатия ε, равным отношению площади сжатого поперечного сечения струи к площади отверстия:
;
Скорость истечения:
;
где ϕ – коэффициент скорости:
; ;
Произведение коэффициентов ε и ϕ принято обозначать буквой µ и называть коэффициентом расхода:
;
Из этого следует, что расход жидкости равен:
или .
39.
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода.
Повышение давления при гидравлическом ударе определяется по формуле Жуковского:
;
Где с – скорость распространения ударной волны:
