26. Графики Никурадзе. Определение коэффициента Дарси опытным путём.

Важные экспериментальные исследования, посвященные изучению зависимости коэффициента Дарси  от числа Re и относительной шероховатости, были проведены Никурадзе для шероховатых труб. В опытах были измерены потери напора и расход, вычислены средние ско­рости потоков и коэффициенты . Результаты Никурадзе показаны на рисунке. По оси абсцисс отложены значения lg Re и по оси ординат lg(100). Представление опытных данных в таких коорди­натах позволяет по углу наклона прямых (в частности, I и II) получить показатель степени в степенной зависимости  от Re. Все опытные точки, полученные Никурадзе, до lgRe=3,35 (Re<2300, ламинарный режим движения) незави­симо от шероховатости стенок труб располагаются на пря­мой. Это значит, что при ламинарном движении  не зави­сит от шероховатости трубы. При Re 2300–3000 (lgRe = 3,35–3,5) происходит переход от ламинарного режима к турбулентному.

Таким образом, исследования, выполненные Никурадзе, наглядно свидетельствуют о наличии различных областей сопротивления при напорном движении в трубах.

27. График Мурина. Определение коэффициента Дарси опытным путем.

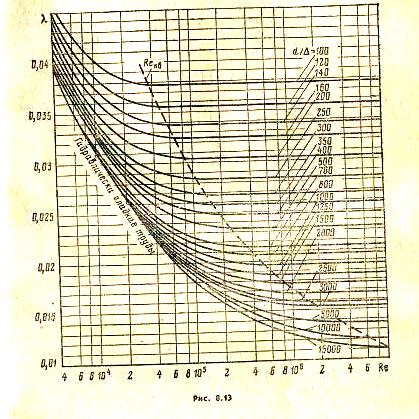
Опыты Никурадзе проводились на трубах, снабжённых искусственной шероховатостью. Для натуральных шероховатых труб закон изменения 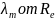получается несколько иным, без подъёма кривых после отклонения их от закона для гладких труб. Различие в характере кривых, объясняется тем, что в натурной трубе бугорки шероховатости имеют различную высоту и при увеличении числа 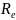начинают выступать за пределы ламинарного слоя не одновременно, а при разных . Ввиду этого переход от линии, соответствующей сопротивлению гладких труб, к горизонтальным прямым, соответствующим квадратичному закону, происходит для натуральных труб более плавно, без провала кривых, характерного для графика Никурадзе.

28. Виды местных сопротивлений. Определение потерь напора на местные сопротивления. Вывод общего уравнения Вейсбаха.

Простейшие местные сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным и постепенным. Более сложные случаи местных сопротивлений представляют собой соединения или комбинации простейших сопротивлений.

Потерю на трение можно выразить по формуле для гидравлических потерь, т.е. ,

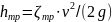однако удобнее коэффициент 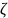связать с относительной длиной трубы .

.

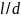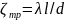В результате формула примет вид

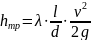
эту формулу обычно называют формулой Вейсбаха.

30. Явление кавитации. Критическое число кавитации.

В некоторых случаях при движении жидкости в закрытых руслах происходят явления, связанные с изменением агрегатного состояния жидкости, т.е. с превращением ее в пар, а также с выделением из жидкости растворенных в ней газов. Например, при течении жидкости через местное сужение трубы увеличивается скорость и падает давление. Если абсолютное давление при этом достигает значения, равного давлению насыщенных паров этой жидкости при данной температуре, или давление, при котором начинается выделение из нее растворенных газов, то в данном месте потока начинается интенсивное парообразование и выделение газов. Это местное нарушение сплошности течения с образованием паровых и газовых пузырей, обусловленное местным падением давления в потоке, называется кавитацией.

,

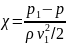Значение , при котором в местном сопротивлении начинается кавитация, называется критическим числом кавитации.