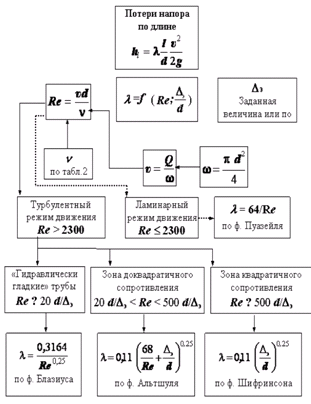
- •20. Коэф. Дарси в случае начального участка.
- •15. Геометрический смысл ур-ия Бернулли.
- •16. Геом. Элементы живого сечения.
- •17. Опыты Рейнольдса.
- •18. Потери напора.
- •19. Коэффициент Дарси при ламинарном напорном движении.
- •29. Определение коэффициентов местных сопротивлений для внезапного и плавного расширения, внезапного и плавного сужения, поворота трубы на
- •26. Графики Никурадзе. Определение коэффициента Дарси опытным путём.
- •27. График Мурина. Определение коэффициента Дарси опытным путем.
- •28. Виды местных сопротивлений. Определение потерь напора на местные сопротивления. Вывод общего уравнения Вейсбаха.
- •30. Явление кавитации. Критическое число кавитации.
- •31. Уравнение Бернулли для потока реальной жидкости
- •32. Дифференциальные уравнения движущейся идеальной жидкости(уравнение л. Эйлера). Вывод уравнений.
- •40. Определение превышения давления в трубопроводе при гидроударе. Фаза и период гидроудара.
- •41. Прямой и непрямой гидроудар. Определение превышения давления.
- •42.Устройство и принцип действия гидротарана.
- •43.Способы борьбы с возникновением гидроудара в трубопроводе.
- •44. Гидравлический расчет трубопроводов. Трубопроводы простые и сложные, короткие и длинные.
- •45). Построение трубопроводной характеристики. Статический и потребный напор.
- •46). Построение трубопроводной характеристики при параллельном и последовательном соединении коротких трубопроводов.
- •47). Расчет длинных трубопроводов. Определение магистрали. Понятие коэф. Расхода. Построение трубопроводной характеристики в случае тупикового трубопровода.
- •49). Основные теории подобия. Геометрическое, кинематическое и динамическое подобие. Критерии подобия: числа Рейнольдса, Вебера, Струхаля, Маха, Фруда, Эйлера, Ньютона.
- •70. Кинематика частицы жидкости в канале центробежного насоса
- •72. Вывод основного уравнения лопастных машин
- •73. Влияние формы лопастей центробежного насоса на напор. Коэффициент закручивания. Коэффициент реактивности.
- •75. Определение гидравлических потерь в лопастном насосе. Действительный напор с учётом потерь.
- •76. Характеристики центробежного лопастного насоса.
- •77. Кавитационные испытание лопастного насоса.
- •78. Гидродинамическое подобие в лопастных насосах.
18. Потери напора.
Потери удельной энергии (напора), затрачиваемой на преодоление сопротивлений движению вязкой жидкости (гидравлических сопротивлений), слагаются из потерь двух видов:
1) потерь напора на преодоление гидравлических сопротивлений по длине, пропорциональных длине участков русла или трубы, по которым движется жидкость,—потерь по длине hдл;
2) потерь напора на преодоление гидравлических сопротивлений в пределах коротких участков в непосредственной близости к тем или иным местным конструктивным устройствам труб, каналов (вход, выход, расширение, сужение, поворот, трубопроводная арматура, фасонные части и т.п.)—местных потерь напора hм.
Принимается, что общие потери напора в системе труб или русл равны сумме потерь напора по длине отдельных участков и всех местных потерь напора:
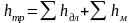
Эти потери энергии (в данном случае удельной) обусловлены переходом механической энергии потока в тепловую. Процесс этот необратим.
Наличие гидравлических сопротивлений при движении вязкой жидкости связано с работой сил трения внутри жидкости. Только благодаря силам трения механическая энергия может перейти в теплоту.
19. Коэффициент Дарси при ламинарном напорном движении.
Из (8.9) можно записать выражение для гидравлического уклона
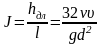 Тогда
имеем
Тогда
имеем
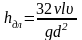
Учитывая,
что общее выражение для потерь напора
по длине труб
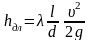
приравняв его
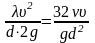
Отсюда
коэффициент Дарси
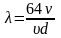
Или
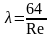
Если выразить число Re через гидравлический радиус R, то
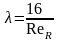 Потери напора по
длине трубы круглого сечения при
равномерном ламинарном движении
пропорциональны средней скорости потока
в первой степени. Это следует из (*), если
подставить в эту формулу
,
и из (8.9б). Опытные данные подтверждают
установленную зависимость hдл
от
в первой
степени.
Потери напора по
длине трубы круглого сечения при
равномерном ламинарном движении
пропорциональны средней скорости потока
в первой степени. Это следует из (*), если
подставить в эту формулу
,
и из (8.9б). Опытные данные подтверждают
установленную зависимость hдл
от
в первой
степени.
22.
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).
Потеря давления в трубопроводе будет равна
![]()
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:
![]()
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
![]()
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
![]()
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
![]()
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу
![]()
23
![]()
Эта формула носит название формулы Дарси-Вейсбаха и является одной из
основных формул гидродинамики.
Коэффициент потерь напора по длине будет равен:
![]()
Запишем формулу Дарси-Вейсбаха в виде:
![]()
Величину![]() называют гидравлическим уклоном, а
величину
называют гидравлическим уклоном, а
величину![]() называ-
называ-
ют коэффициентом Шези.
![]()
Величина
![]() имеет размерность скорости и носит
название динамической
имеет размерность скорости и носит
название динамической
скорости жидкости.
Тогда
коэффициент трения (коэффициент Дарси):![]()
24.
Эквивалентная
шероховатость
– это искусственная равномерная
шероховатость с такой высотой (диаметром)
зерен
![]() при
которой в области квадратичного
сопротивления (где
при
которой в области квадратичного
сопротивления (где
![]() зависит
только от шероховатости и не зависит
от
зависит
только от шероховатости и не зависит
от
![]() )
значение коэффициента
равно
его значению при естественной
шероховатости.
)
значение коэффициента
равно
его значению при естественной
шероховатости.
Гидравлически гладкие и шероховатые трубы. Состояние стенок трубы в
значительной мере влияет на поведение жидкости в турбулентном потоке. Так при
ламинарном
движении 
жидкость движется медленно и плавно, спокойно обтекая на своём пути
незначительные препятствия. Возникающие при этом местные сопротивления
настолько ничтожны, что их величиной можно пренебречь. В турбулентном же
потоке такие малые препятствия служат источником вихревого движения жидкости,
что приводит к возрастанию этих малых местных гидравлических сопротивлений,
которыми мы в ламинарном потоке пренебрегли. Такими малыми препятствиями на
стенке трубы являются её неровности. Абсолютная величина таких неровностей
зависит от качества обработки трубы. В гидравлике эти неровности называются
выступами
шероховатости, они обозначаются литерой![]()
.
В зависимости от соотношения толщины ламинарной плёнки и величины выступов
шероховатости будет меняться характер движения жидкости в потоке. В случае,
когда толщина ламинарной плёнки велика по сравнению с величиной выступов
шероховатости
(![]() ,
,
выступы шероховатости погружены в ламинарную плёнку и турбулентному ядру
течения они недоступны (их наличие не сказывается на потоке). Такие трубы
называются гидравлически гладкими (схема 1 на рисунке). Когда размер выступов
шероховатости превышает толщину ламинарной плёнки, то плёнка теряет свою
сплошность, и выступы шероховатости становятся источником многочисленных
вихрей, что существенно сказывается на потоке жидкости в целом. Такие трубы
называются гидравлически шероховатыми (или просто шероховатыми) (схема 3 на
рисунке). Естественно, существует и промежуточный вид шероховатости стенки
трубы, когда выступы шероховатости становятся соизмеримыми с толщиной
ламинарной
плёнки![]()
(схема 2 на рисунке). Толщину ла-
минарной плёнки можно оценить исходя из эмпирического уравнения
![]()
25