20. Коэф. Дарси в случае начального участка.

Сравнение данной зависимости с формулой Дарси-Вейсбаха

,

позволяет сделать важный вывод: при ламинарном режиме движения жидкости в трубах круглого сечения коэффициент Дарси ? определяется по формуле Пуазейля

. (4.71)

т. е. при ламинарном режиме коэффициент гидравлического трения не зависит от шероховатости стенок трубы и является функцией только числа Re. Теоретические результаты хорошо согласуются с опытными данными для изотермических ламинарных потоков, у которых отсутствует теплообмен с окружающей средой. Благодаря большим силам вязкостного трения обтекание бугорков шероховатости на стенках происходит плавно без отрывов потока, поэтому шероховатость не влияет на потери напора.

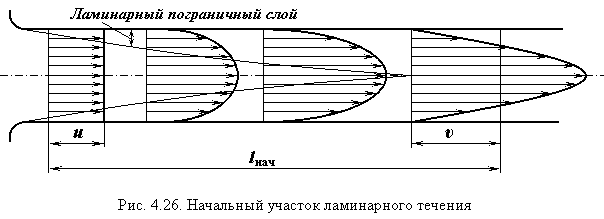
Приведённые соотношения справедливы для стабилизированного ламинарного потока, когда параболический закон скоростей уже установился. Если жидкость поступает в трубу с плавным входом из большого резервуара, то во всех точках входного сечения скорость одинакова (рис. 4.26). По мере движения слои у стенки оказываются заторможенными действиями сил трения, и у стенок образуется пристенный пограничный слой; толщина его возрастает по длине трубы. На начальном участке трубы влияние вязкости распространяется постепенно на все сечения потока. На этом участке в каждом сечении сохраняется ядро потока, где скорости постоянны, и на которое вязкость ещё не влияет. После того как пограничный слой займёт все сечение потока, течение стабилизируется. Длину начального участка приближенно можно определить так:

14. Вывод уравнения Бернулли для элементарной струйки идеальной жидкости.

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости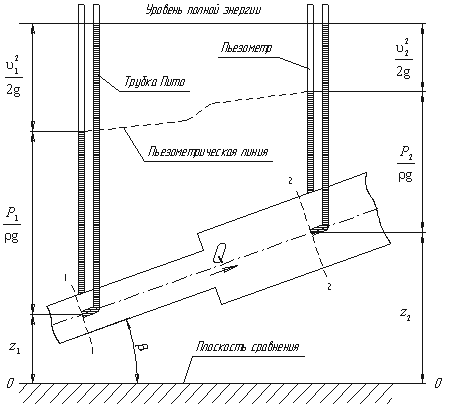

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.1).

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

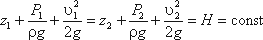
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

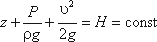
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

15. Геометрический смысл ур-ия Бернулли.

У равнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.1, можно заметить, что z1 и z2 - геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения;

пьезометрические высоты; скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная. С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии: z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;

удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях; удельные кинетические энергии в тех же сечениях. Следовательно, согласно уравнению Бернулли,

полная удельная энергия идеальной жидкости в любом сечении постоянна

Геометрический смысл: - пьезометрический напор, z - напор положения, - скоростной напор.

Для вязкой жидкости: , где hw1-2 - затраты на преодоление сопротивлений между 1 и 2 сечениями - потеря напора.

Энергетический смысл: при u=0 - - основное уравнение гидростатики, так как - удельная энергия давления, а z - удельная энергия положения, то - удельная кинетическая энергия..

Полный напор представляет собой расстояние, измеряемое в единицах длины (метр) от свободной поверхности воды в данной точке до некоторой произвольной горизонтальной плоскости, принятой за начальную. Полный напор включает в себя напор геометрический Hг, пьезометрический Hп и скоростной (скоростным напором мы обычно пренебрегаем, так как он крайне мал). Таким образом, мы получаем напор H:

Линия 1 на рис. 4, характеризующая изменение вдоль течения пьезометрического напора, называется пьезометрической линией. Ее уклон, т.е. изменение пьезометрического напора вдоль пути перемещения жидкости Iп, называется пьезометрическим уклоном. Если движение равномерное, то пьезометрическая линия параллельна напорной и отстоит от нее на расстоянии, соответствующем скоростному напору; в этом случае I = Iп = 0. При увеличении скорости вдоль течения из-за уменьшения площади живого сечения растет скоростной напор, а пьезометрическая линия идет с большим уклоном, чем напорная (I < Iп > 0). Наоборот, с уменьшением скорости при расширении струйки вдоль течения линии сближаются, т.е. пьезометрический уклон становится меньше гидравлического (I > Iп < 0). Пьезометрическая линия может снижаться вдоль течения, идти вверх и быть горизонтальной. Построение пьезометрической и напорной линий широко применяется в решении многих задач, так как это дает возможность быстро устанавливать основные характеристики движения жидкости, причины и степень их изменяемости. Напорная линия всегда падает, а пьезометрическая может опускаться и подниматься ( по направлению потока). Подъем линии должен быть в местах увеличения площадей поперечных сечений потока, где скорость уменьшается, а давление увеличивается