22. Критерий устойчивости Найквиста.

Передаточная функция замкнутой системы:

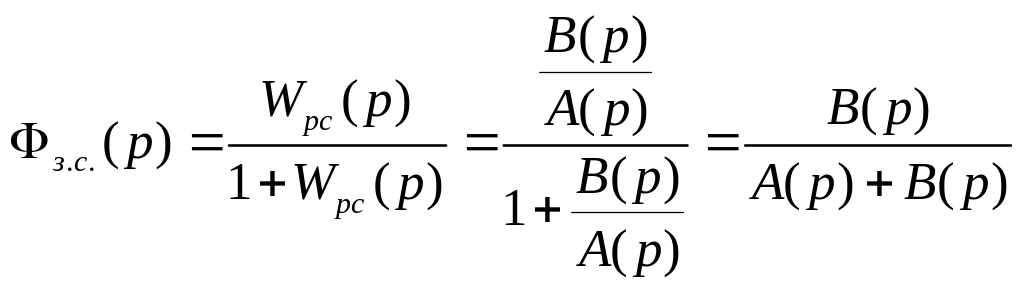
Характеристическое уравнение разомкнутой системы:

Характеристическое уравнение замкнутой системы:

Формулировка критерий Найквиста:

Контур, устойчивый в разомкнутом состоянии, сохранит устойчивость и после замыкания, если его КЧХ в разомкнутом состоянии не охватывает точки -1, j₀.

23. Запас устойчивости лдс и способы его оценки

Запас устойчивости ЛДС – это её оценочная характеристика, определяющая интенсивность затухания переходных процессов, возникающих в системе.

Интенсивность затухания колебаний в переходном процессе может быть оценена численно уменьшением каждой очередной амплитуды колебаний по сравнению с предыдущей , направленных в одну сторону. Полученный таким образом показатель

был назван степенью затухания колебания. Он связан с соответствующей парой комплексный корней характеристического уравнения соотношением

где - коэффициент, названный корневым показателем колебательности.

Частотный показатель колебательности – это отношение максимального (пикового) значения АЧХ к её значению при нулевой частоте. Максимальное значение АЧХ – это значение при частоте резонанса .

Связь с корневым показателем колебательности:

ЛДС, переходная характеристика которой при стремится к новому установившемуся значению, называется статической, или обладающей свойством самовыравнивания.

ЛДС, переходная характеристика которой при не стремится к новому установившемся значению (постоянно убывает или возрастает), называется астатической. При этом, если то система обладает астатизмом 1-го порядка. Если - астатизмом порядка .

24. Прямые и косвенные показатели качества переходных процессов в лдс.

Прямые показатели

(показатели, определяемые непосредственно по переходным процессам)

1. Статическая ошибка регулирования.

Определяется по значению выходной величины:

А) при внешнем возмущении:

Б) при заданном возмущении:

2. Динамическая ошибка регулирования.

Определяется как максимальное по модулю отклонение регулируемой переменной от установившегося значения за период наблюдения процесса:

3. Степень затухания переходного процесса.

Под степенью затухания понимается показатель

Который характеризует запас устойчивости системы и интенсивность уменьшения амплитуды колебаний переходного процесса с приближением к установившемуся значению.

система находится на границе устойчивости, и колебания носят незатухающий характер.

переходный процесс носит, как правило, апериодический (неколебательный) характер, и система обладает большим запасом устойчивости.

4. Время регулирования.

Время регулирования определяется по условию:

где зона нечувствительности системы.

Косвенные показатели

(показатели, определяемые запасом устойчивости системы)

1. Степень устойчивости (корневой):

Определяется как минимальное значение действительной части корня характеристического уравнения:

Параметр определяет длительность переходных процессов: с уменьшением возрастает время регулирования .

2. Показатель колебательности (корневой):

Определяется как минимальное по всем корням характеристического уравнения отношение действительной и мнимой части корня:

При приближении корней к мнимой оси система будет находиться на границе устойчивости, т.е. будут иметь место соотношения:

При приближении корней к действительной оси запас устойчивости системы будет увеличиваться с выполнением соотношений:

3. Показатель колебательности (частотный):

Определяется в соответствии с соотношениями:

Частотный показатель колебательности – это отношение максимального (пикового) значения АЧХ к её значению при нулевой частоте. Максимальное значение АЧХ – это значение при частоте резонанса .

Связь с корневым показателем колебательности:

Заданному значению в комплексной плоскости соответствует «запретная» область в окрестности «опасной» точки , в которую не должен заходить годограф КЧХ разомкнутой системы.

13