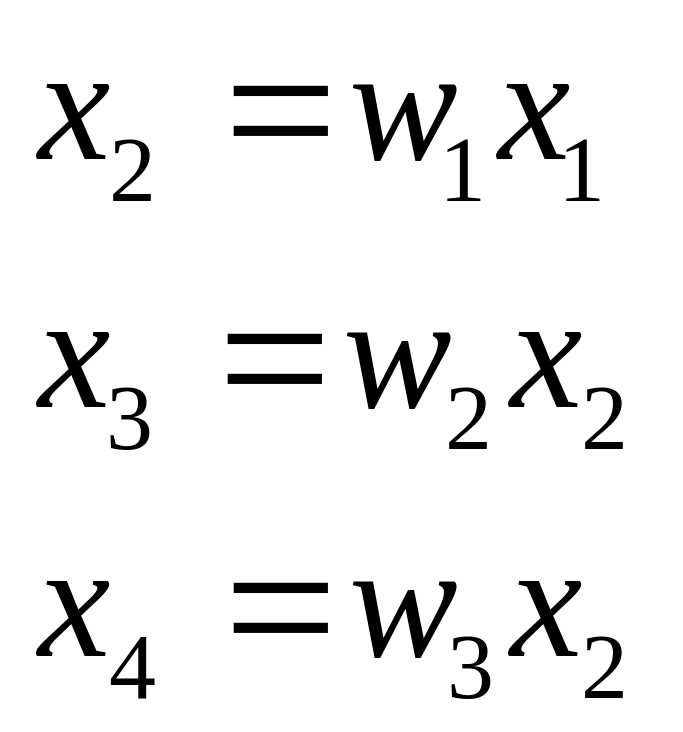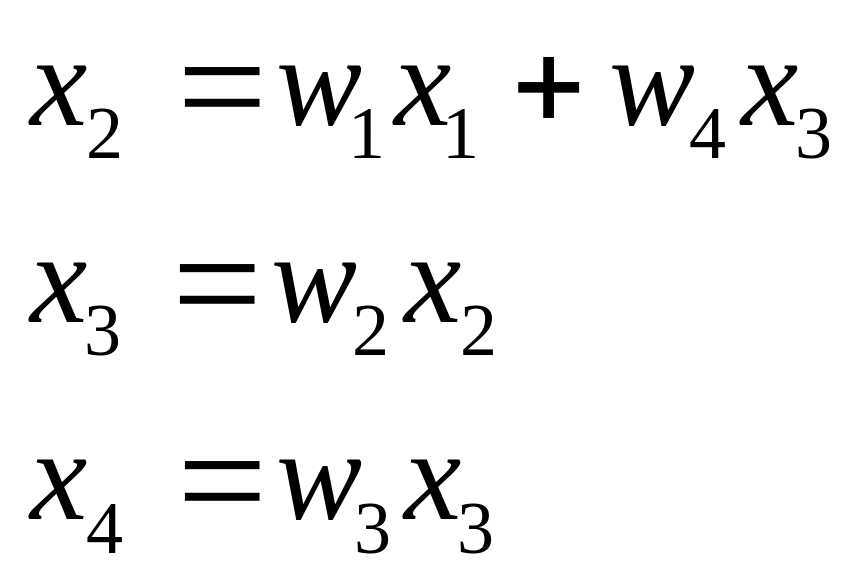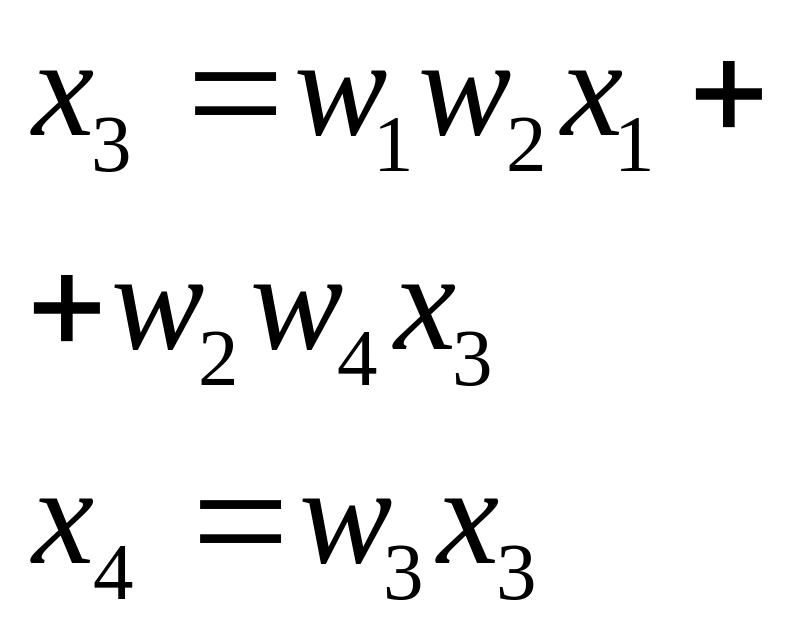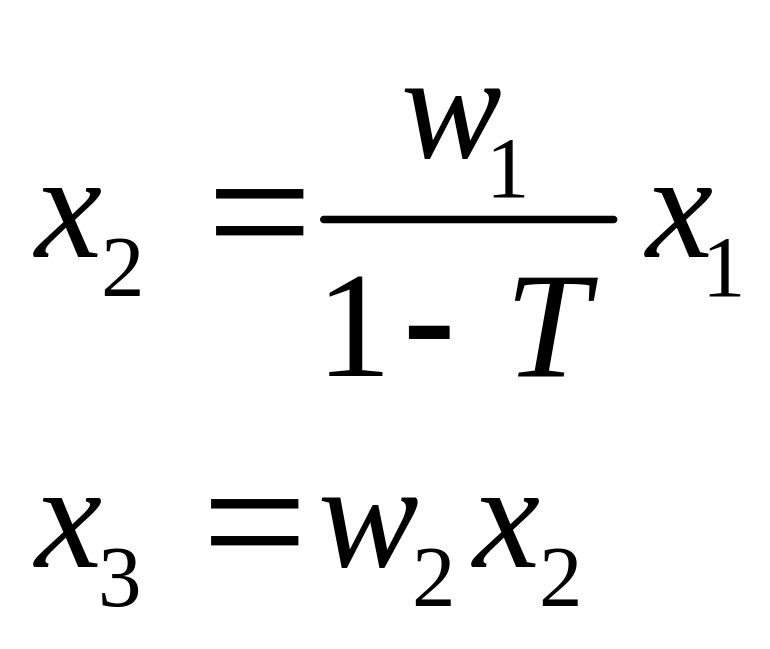13. Способы соединения звеньев и соответствующие им эквивалентные характеристики систем.

1. Последовательное соединение

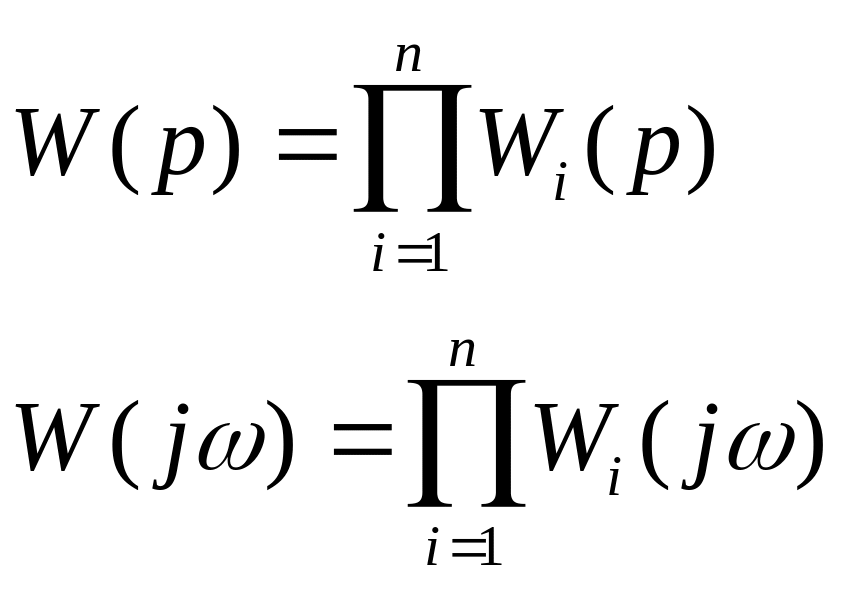
2. Параллельное соединение

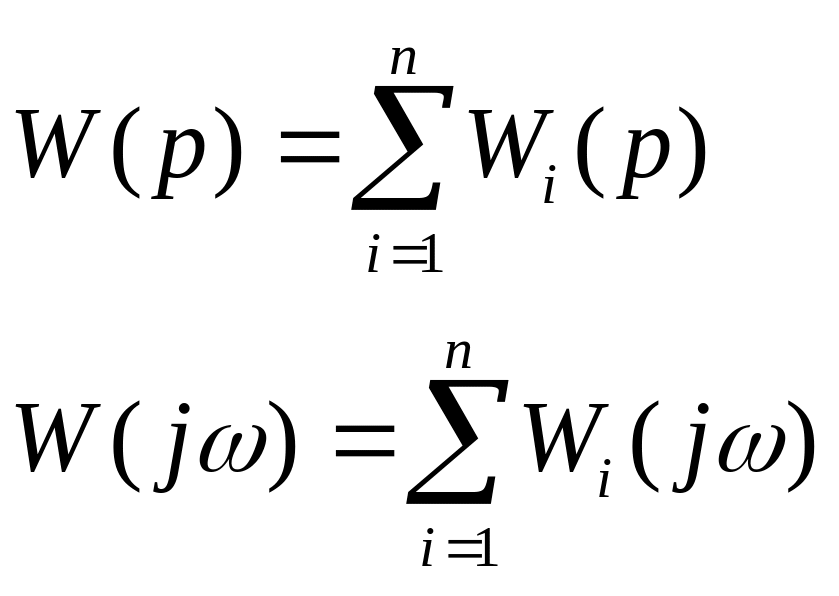
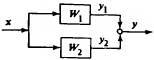
3 . Соединение с обратной связью

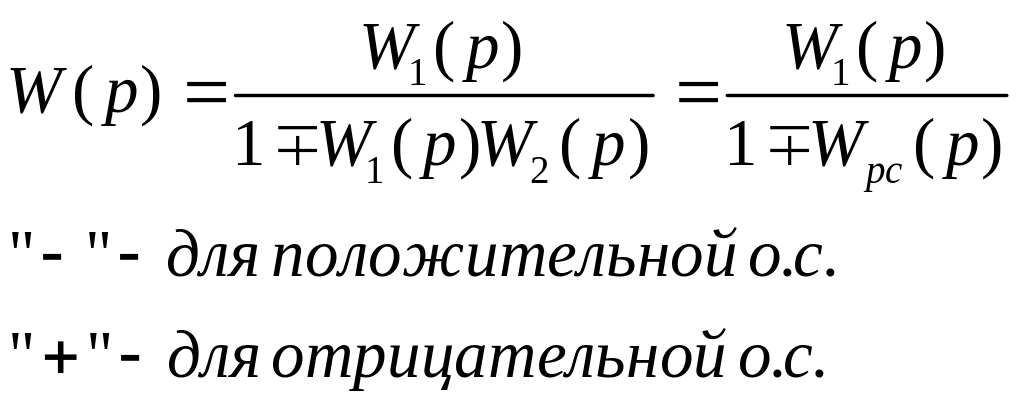
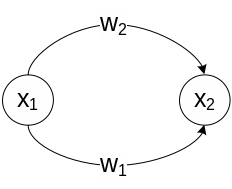
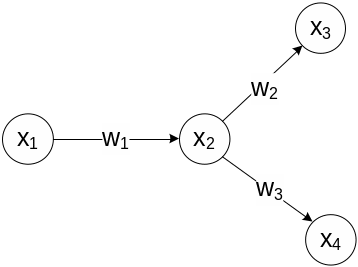
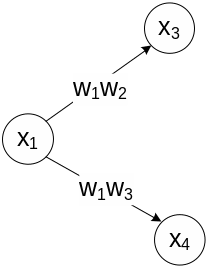
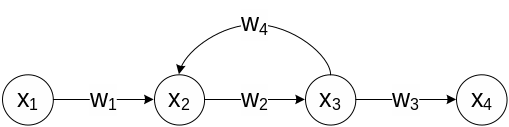
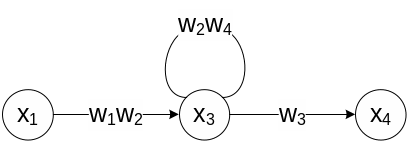
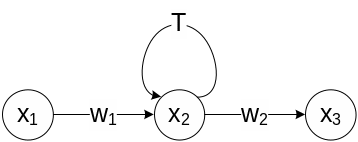
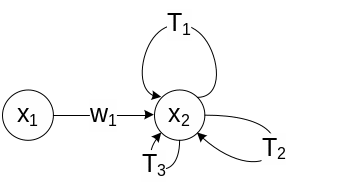
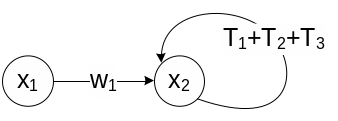
14. Сигнальный граф в задачах описания топологии (структуры) сложной системы и типовые способы эквивалентирования характеристик динамических систем.

Сигнальным графом называется ориентированный граф, вершинами которого служат сигналы, а дугами являются операторы преобразования, т.е. модели динамических и статических элементов.

Операция эквивален-тирования	Система уравнений		Сигнальный граф
	Исходная	Эквивалентная	Исходный	Эквивалентный
1. Замена при последовательном соединении
2. Замена при параллельном соединении
3. Устранение простого узла
4. Исключение контура
5. Исключение петли
6. Объединение петель

15. Устойчивость линейных динамических систем.

Устойчивость – это способность динамической системы, перемещённой внешней силой в некоторое ненулевое состояние возвращаться в исходное нулевое состояние после устранения возмущения.

При любом реакция системы: где свободная, а вынужденная составляющая решения.

действительные и различные корни . Необходимо, чтобы

16. Необходимые условия устойчивости лдс.

Для того, чтобы ЛДС, передаточная функция которой имеет дробно-рациональный вид была устойчивой, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные действительные части, т.е.:

18. Критерии устойчивости

Для анализа устойчивости ЛДС кроме непосредственного определения корней характеристических уравнений используются критерии устойчивости.

Критерием устойчивости называется математический способ, обеспечивающий возможность оценки устойчивости системы по её характеристическому уравнению без прямого вычисления корней.

Различают 2 вида критериев: алгебраические и частотные.

Алгебраический критерий устойчивости Рауса-Гурвица: для того, чтобы ЛДС была устойчивой, необходимо, чтобы все определители матрицы Рауса-Гурвица из коэффициентов были положительными.

Частотный критерий устойчивости Михайлова: ЛДС устойчива, если годограф Михайлова , начиная своё движения с действительной положительной полуоси и нигде не обращаясь в 0, последовательно проходит против часовой стрелки число квадрантов, равное порядку .

Частотный критерий Найквиста: замкнутая ЛДС устойчива, если «опасная» точка лежит вне пределов контура, охватываемого годографом КЧХ разомкнутой ЛДС.

19. Критерий устойчивости Рауса-Гурвица.

Пусть дано характеристическое уравнение ЛДС:

Для анализа устойчивости составляют матрицу Рауса-Гурвица из коэффициентов данного уравнения. Формируются миноры и вычисляются определители:

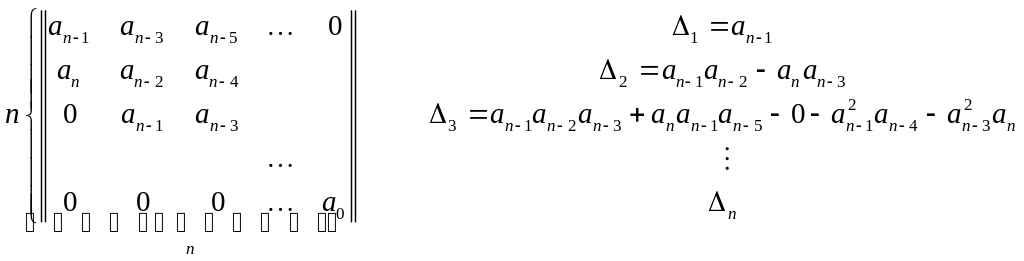
Для того, чтобы ЛДС была устойчивой, необходимо, чтобы все определители были положительными, т.е.:

Система находится на границе устойчивости, если какой-либо а все остальные – положительны.

Система неустойчива, если какой-либо из определителей

21. Критерий устойчивости Михайлова.

Если система находится на границе устойчивости, то это свидетельствует о наличии среди корней её характеристического уравнения пары чисто мнимых корней: . Подставив один из этих корней в характеристическое уравнение, получим уравнение:

Будем рассматривать левую часть этого уравнения как функцию мнимой переменной :

Для фиксированного значения она отображается в комплексной плоскости вектором, получившем название характеристического; при изменении от нуля до бесконечности конец этого вектора очерчивает кривую, называемую годографом Михайлова.

Критерий формулируется следующим образом:

С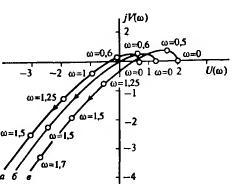 истема устойчива, если при изменении от нуля до бесконечности годограф Михайлова, начинаясь на положительной вещественной полуоси, проходит последовательно против часовой стрелки квадрантов комплексной плоскости (где степень характеристического уравнения), или, иначе говоря, характеристический вектор поворачивается против часовой стрелки на

В качестве примера на показаны годографы Михайлова системы третьего порядка для трёх случаев: система устойчива – годограф проходит против часовой стрелки последовательно три квадранта (кривая а); система находится на границе устойчивости, генерируя незатухающие синусоидальные колебания с частотой, при которой годограф проходит через начало координат (кривая б); система неустойчива – годограф проходит три квадранта, но в ненадлежащей последовательности (кривая в).

Годограф Михайлова применяется для анализа устойчивости любых динамических систем, передаточная функция которых имеет дробно-рациональный вид.