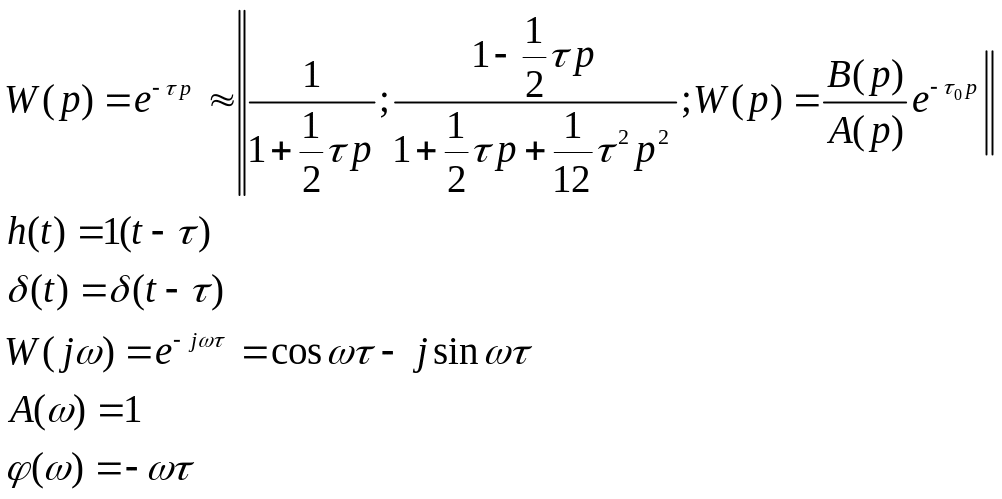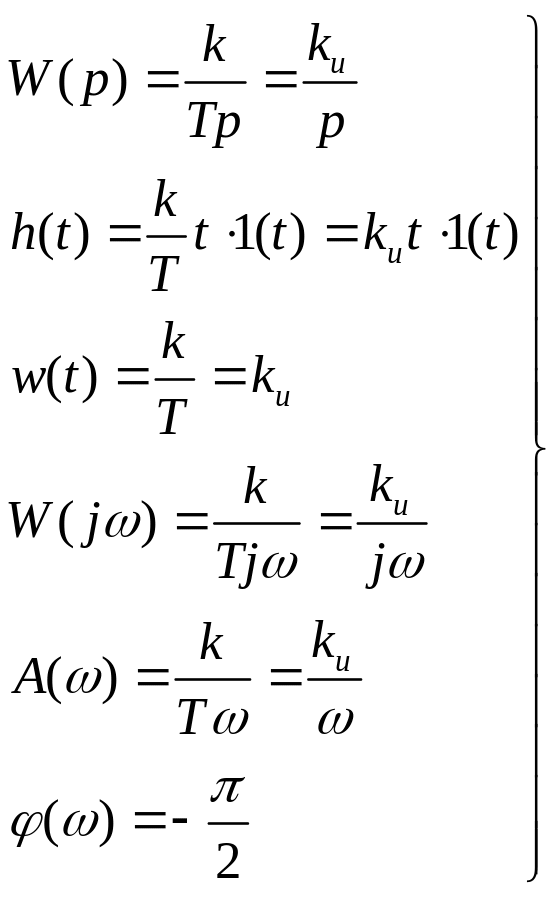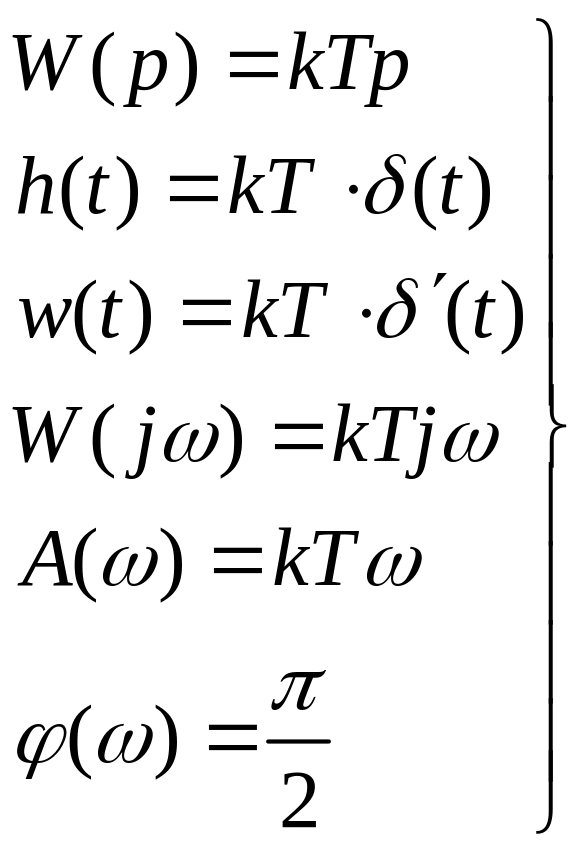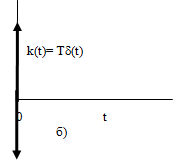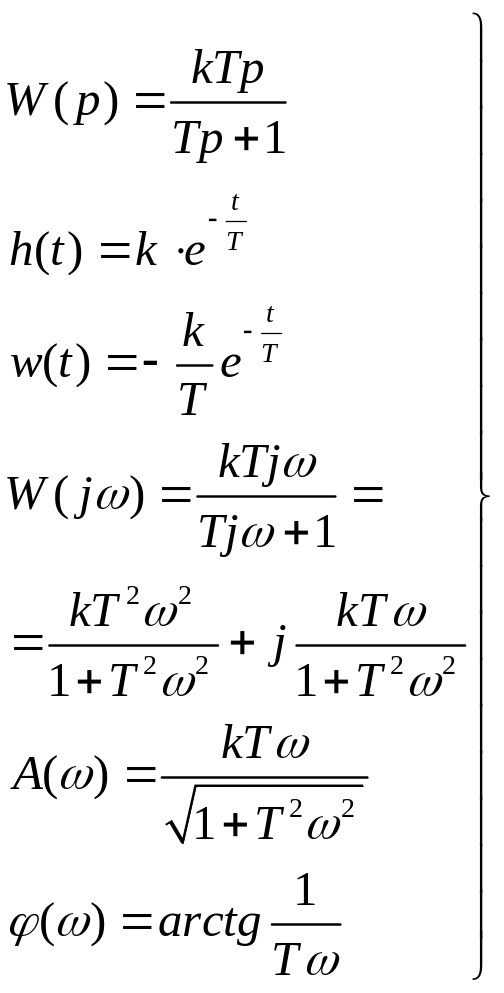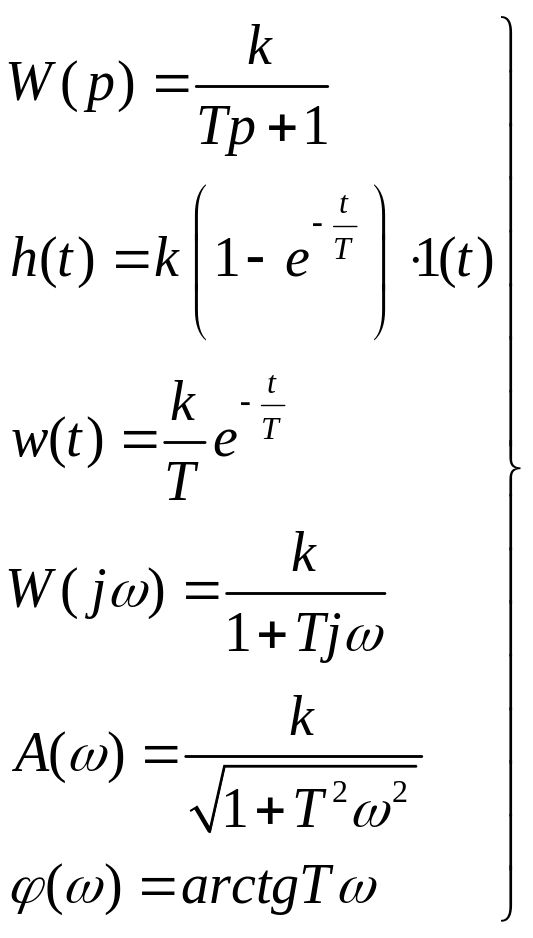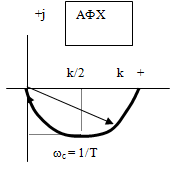- •1. Объект управления
- •2. Принцип управления «по возмущению».
- •3. Принцип управления «по отклонению».
- •4. Динамическая характеристика линейной системы управления (лдс).
- •5. Передаточная функция линейной стационарной непрерывной динамической системы
- •6. Классификация типовых детерминированных воздействий, используемых для исследования динамических систем
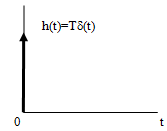
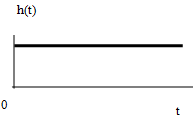
- •7. Переходная характеристика динамической системы
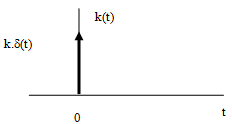
- •8. Импульсная характеристика динамической системы (функция веса).
- •10. Представление кчх в декартовой и полярной системах координат. Частные формы кчх: вчх, мчх, ачх, фчх.
- •11. Интеграл свёртки (Дюамеля).
- •12. Типовые звенья в динамических системах
- •13. Способы соединения звеньев и соответствующие им эквивалентные характеристики систем.
- •14. Сигнальный граф в задачах описания топологии (структуры) сложной системы и типовые способы эквивалентирования характеристик динамических систем.
- •15. Устойчивость линейных динамических систем.
- •16. Необходимые условия устойчивости лдс.
- •18. Критерии устойчивости
- •19. Критерий устойчивости Рауса-Гурвица.
- •21. Критерий устойчивости Михайлова.
- •22. Критерий устойчивости Найквиста.
- •23. Запас устойчивости лдс и способы его оценки
- •24. Прямые и косвенные показатели качества переходных процессов в лдс.
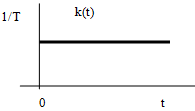
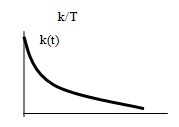
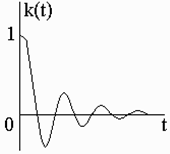
8. Импульсная характеристика динамической системы (функция веса).
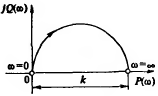
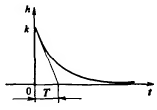
Импульсной характеристикой называется
реакция системы на единичное импульсное
воздействие![]()
![]()
9. Комплексная частотная характеристика (КЧХ) динамической системы.
КЧХ системы называют комплексную функцию
частоты, получаемую из передаточной
функции системы путём замены![]() .
Модуль КЧХ равен амплитудной частотной
характеристике (АЧХ), а аргумент –
фазовой частотной характеристике (ФЧХ).
.
Модуль КЧХ равен амплитудной частотной
характеристике (АЧХ), а аргумент –
фазовой частотной характеристике (ФЧХ).
А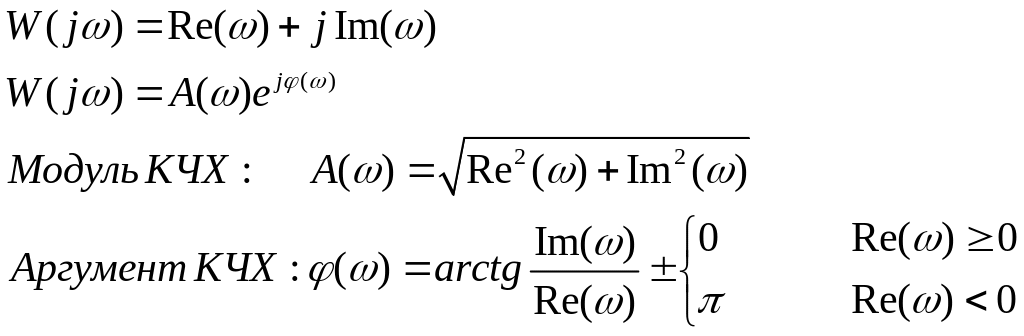 ЧХ
– зависимость отношения амплитуд
колебаний на входе и выходе системы от
частоты.
ЧХ
– зависимость отношения амплитуд
колебаний на входе и выходе системы от
частоты.
ФЧХ – зависимость сдвига по фазе между колебаниями на выходе и входе системы от частоты.
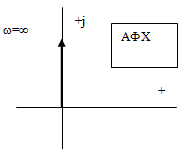
10. Представление кчх в декартовой и полярной системах координат. Частные формы кчх: вчх, мчх, ачх, фчх.
В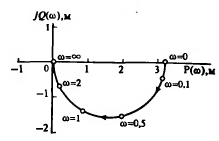 етвь
КЧХ для отрицательных частот является
зеркальным отражением относительно
вещественной оси его ветви для
положительных частот. Поэтому при
практических расчётах обычно ограничиваются
построением КЧХ только для положительных
частот.
етвь
КЧХ для отрицательных частот является
зеркальным отражением относительно
вещественной оси его ветви для
положительных частот. Поэтому при
практических расчётах обычно ограничиваются
построением КЧХ только для положительных
частот.
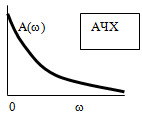
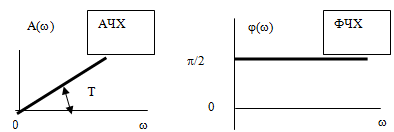
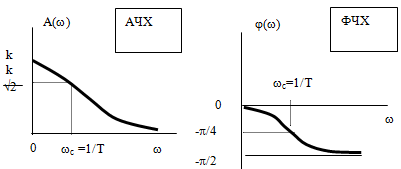
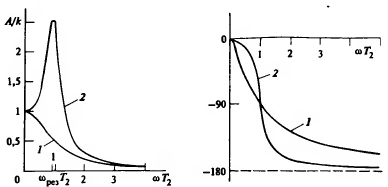
АЧХ – амплитудная частотная характеристика (зависимость модуля КЧХ от частоты).
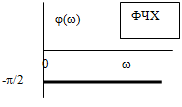
ФЧХ – фазовая частотная характеристика (зависимость аргумента КЧХ от частоты).
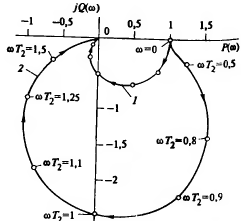
Рис. 3. КЧХ апериодического звена.
ВЧХ – вещественная частотная характеристика (зависимость вещественной части КЧХ от частоты).
МЧХ – мнимая частотная характеристика (зависимость мнимой частотной части КЧХ от частоты).
11. Интеграл свёртки (Дюамеля).
Интеграл Дюамеля позволяет определять
реакцию системы на неизвестное или
известное воздействие
![]() в
текущем времени (в реальном, замедленном
или ускоренном масштабе, в зависимости
от мощности вычислительного инструмента
и желания исследователя) по ее переходной
функции
в
текущем времени (в реальном, замедленном
или ускоренном масштабе, в зависимости
от мощности вычислительного инструмента
и желания исследователя) по ее переходной
функции![]() :
:
![]()
Как видно, интеграл Дюамеля оперирует с сигналами, начавшимися в нулевой момент времени или позднее и может учитывать одно начальное условие (выходной сигнал в начальный момент времени), но не значения младших производных выходного сигнала в нулевой момент времени, которые предполагаются нулевыми.
Интеграл свертки
можно рассматривать как вариант интеграла
Дюамеля, в котором под интегралом
проведено интегрирование по частям.
Это позволяет выразить выходной сигнал
системы через ее весовую функцию![]()
![]()
12. Типовые звенья в динамических системах
Пропорциональное звено:
Описывается уравнением вида:![]() ,
где
,
где![]() коэффициент
пропорциональности (усиления).
коэффициент
пропорциональности (усиления).
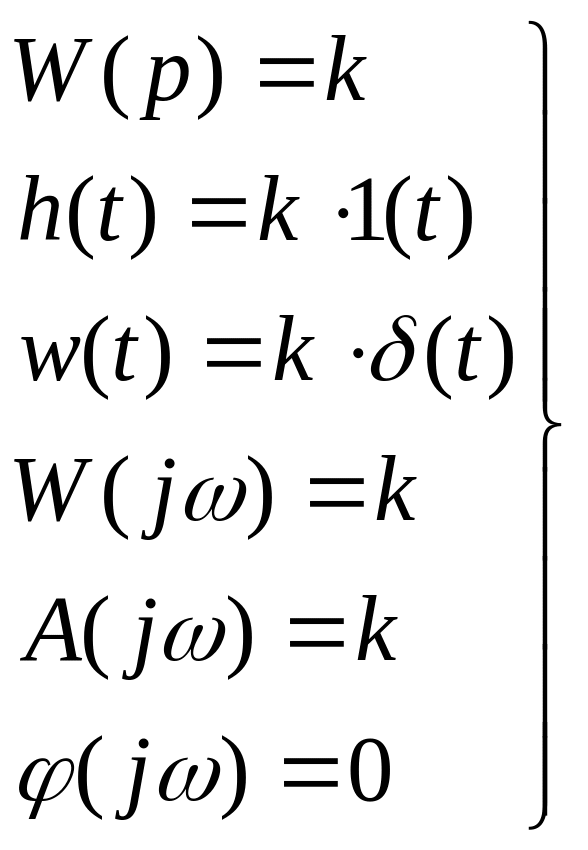
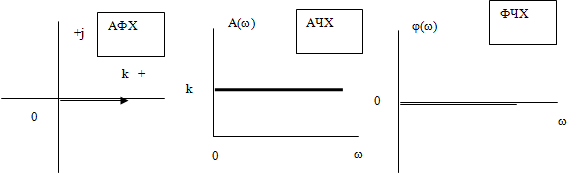
Примеры: усилители постоянного тока, потенциометры.
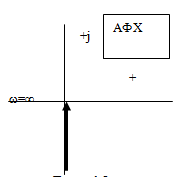
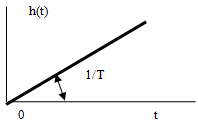
Интегрирующее звено:
Описывается уравнением вида:![]() или
или![]() .
.
|
|
|
Примеры: операционный усилитель, двигатели с переменной скоростью. |
||
Дифференцирующее (идеальное) звено:
Описывается уравнением вида:![]() .
.
|
|
|
Примеры: операционный усилитель, тахогенератор. |
||
Идеальное дифференцирующее звено является физически не реализуемым. В реальных звеньях такой вид характеристики могут иметь только в ограниченном диапазоне частот.
Реальное дифференцирующее звено:
Описывается уравнением вида:![]() .
.
|
|
|
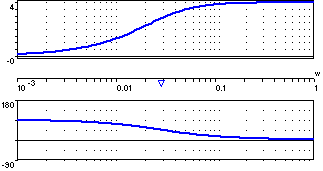
АЧХ – вверху, ФЧХ – внизу. Примеры: корректирующая обратная связь в регуляторе паровой машины. |
||
Для того, чтобы свойства РД-звена
приближались к свойствам идеального,
необходимо одновременно увеличивать
коэффициент передачи![]() и
уменьшать постоянную времени
и
уменьшать постоянную времени![]() так,
чтобы их произведение оставалось
постоянным
так,
чтобы их произведение оставалось
постоянным![]() .
.
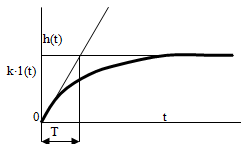
Апериодическое звено:
Описывается уравнением вида:![]() .
.
|
|
|
Примеры: механические демпферы. |
||
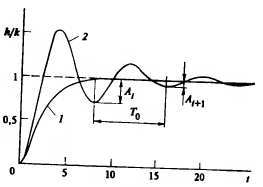
Инерционное звено второго порядка.
Описывается уравнением:![]()
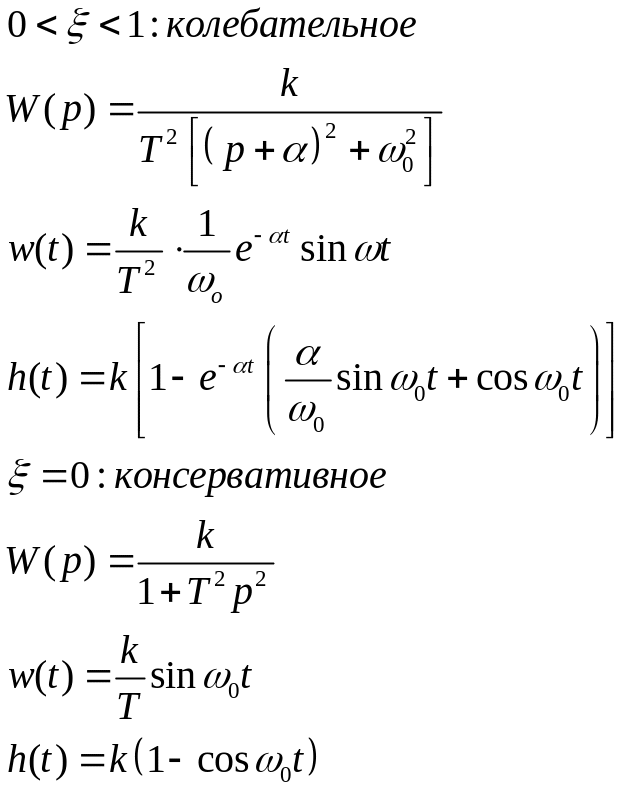
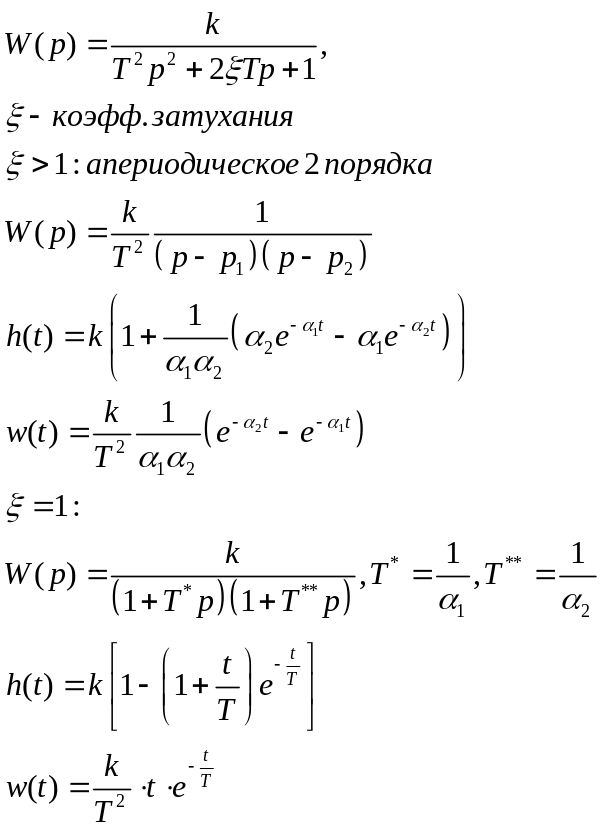
![]() апериодическое
2 порядка
апериодическое
2 порядка
![]() колебательное
звено
колебательное
звено
![]() консервативное
звено
консервативное
звено
![]() неустойчивое
звено
неустойчивое
звено
Звено |
Коэфф. затухания
|
Корневой пок-тель колебательности
|
Частотный п-тель колебательности
|
Степень затухания
|
|
Консервативное |
0 |
0 |
|
0 |
|
Колебательное 1 |
0.215 |
0.221 |
2.38 |
0.75 |
|
Колебательное 2 |
0.344 |
0.367 |
1.55 |
0.9 |
|
Апериодическое |
|
|
1 |
1 |
|
|
|
||||
|
|||||
Интегродифференцирующее звено:
Описывается уравнением:![]()
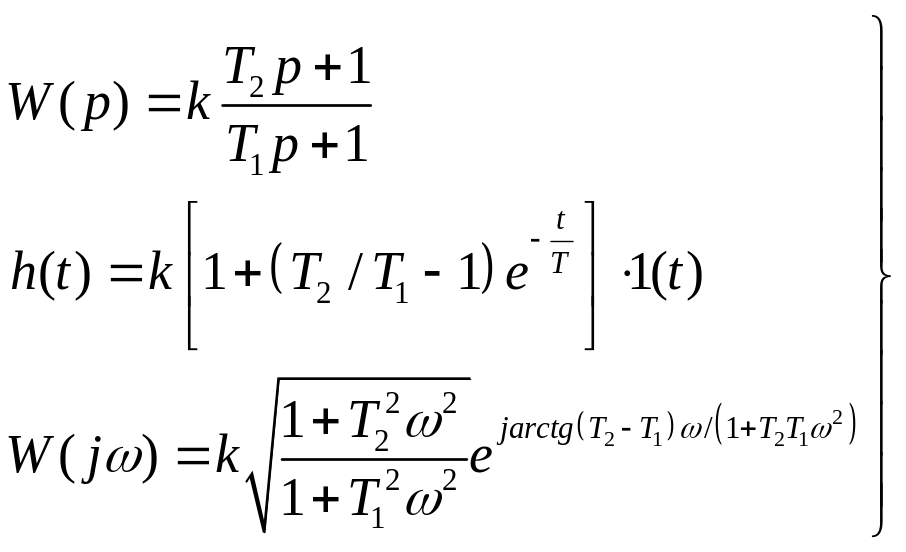
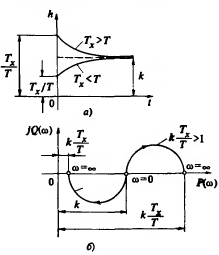
Запаздывающее звено:
![]()