52.Сформулюйте першу теорему двоїстості й дайте економічну інтерпретацію.

Якщо одна з пари двоїстих задач має оптимальний план, то й інша має оптимальний план, причому екстремальні значення цільових функцій рівні:

.

Якщо одна із двоїстих задач нерозв'язна внаслідок необмеженості цільової функції на множині припустимих планів, то система обмежень іншої задачі суперечлива.

Якщо сукупність обмежень однієї із двоїстих задач суперечлива, то або функція мети іншої задачі не обмежена на множині припустимих розв'язків, або система обмежень іншої задачі також суперечлива.

Економічний зміст першої теореми подвійності: якщо задача визначення оптимального плану, максимизирующего випуск продукції, розв'язна, те розв'язна й задача визначення оцінок ресурсів. Причому вартість випущеної продукції, отриманої при реалізації оптимального плану, збігається із сумарною оцінкою ресурсів. Збіг значень цільових функцій для відповідних планів пари двоїстих задач досить, щоб ці плани були оптимальними. Оцінки в цьому випадку виступають як інструмент балансування витрат і результатів. Двоїсті оцінки мають тем властивістю, що вони гарантують рентабельність оптимального плану, тобто рівність загальної оцінки продукції й ресурсів, і обумовлюють збитковість усякого іншого плану, відмінного від оптимального.

53.Сформулюйте й дайте економічну інтерпретацію другої теореми двоїстості.

Для того щоб плани Х^* і В^* пари двоїстих задач були оптимальними, необхідно й достатнє виконання умов:

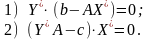
Умови 1 і 2 називаються умовами нетвердості, що доповнює.

Дамо економічну інтерпретацію умовам нетвердості, що доповнює.

Згідно з умовою 1, якщо в оптимальній системі оцінок якийсь ресурс i одержить відмінну від нуля оцінку те відповідно до оптимального плану виробництва прямої задачі цей ресурс, будучи дефіцитним, буде витрачений повністю:

Якщо якийсь i-й ресурс витрачається не повністю (надлишковий), тобто

те його оцінка дорівнює нулю,

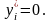
Звідси випливає, що оцінки оптимального плану – це захід дефіцитності ресурсів.

Згідно з умовою 2, якщо деякий продукт j входить в оптимальний план виробництва (xj^*>0), те при оптимальній системі оцінок двоїстої задачі витрати ресурсів на його виготовлення збігаються з вартістю цього продукту, тобто

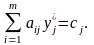
Якщо витрати ресурсів на випуск якого-небудь продукту j перевищують його вартість,

те цей продукт не проводиться, тобто xj^*=0.

Звідси висновок:

Дефіцитний ресурс (повністю використаний у виробництві) має позитивну оцінку, а ресурс недефіцитний (надлишковий) має нульову оцінку.

Для ілюстрації застосування другої теореми подвійності при розгляді пари двоїстих задач розглянемо наступні приклади.

54.Перерахуйте властивості подвійних оцінок. У чому полягає їх економічний сенс.

В оптимальному плані двоїстої задачі значення змінної чисельно рівне приватної похідної функції 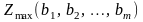по відповідному до аргументу 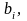тобто

З теореми про оцінки випливає, що при малій зміні правої частини i-го обмеження в системі обмежень ЗЛП максимальне значення цільової функції змінюється на величину

Зокрема, при 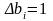маємо

Стосовно до задачі оптимального використання ресурсів можна сказати, що двоїста оцінка i- го ресурсу приблизно дорівнює приросту оптимального прибутку, що виникає за рахунок збільшення об'єму i-го ресурсу на одиницю.

З теореми також випливає, що якщо зміниться об'єм кожного ресурсу на величину , те ці зміни приведуть до сумарної зміни прибутки , який може бути обчислене по формулі:

Ця формула має місце лише тоді, коли при зміні величин bi значення змінних в оптимальному плані відповідної двоїстої задачі залишаються незмінними, тому становить інтерес визначити такі інтервали зміни кожного з вільних членів bi, у яких оптимальний план двоїстої задачі не міняється. Такі інтервали називають інтервалами стійкості двоїстих оцінок.