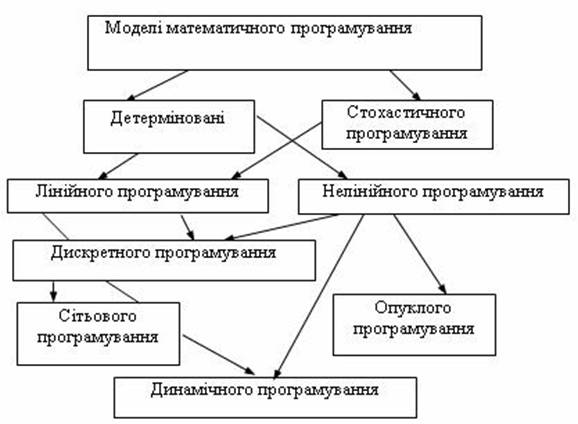
26. Коротка класифікація моделей і методів математичного програмування.

Коротка класифікація моделей програмування

За типом змінних розрізняють задачі математичного програмування з неперервними та дискретними  змінними. Останні створюють окремий клас задач дискретного  програмування, підкласом якого є задачі цілочисельного програмування. 

За фактором часу задачі математичного програмування поділяють на статичні та динамічні. 

В залежності від параметрів моделі розрізняють  детерміновані  та стохастичні моделі програмування. ,

27. Поняття математичної моделі.

Якщо задача має множину розв’язків то необхідно з цієї множини знайти найкращий варіант з цієї множини з точки зору мети. Такі задачі називаються – задачами оптимізації, а найкращий варіант оптимальним. Щоб знайти оптимальний варіант треба перейти від змістової постановки задачи до математичної такий процес називається математичним моделюванням. В результаті такого моделювання складається математична модель. Математичною моделлю називається сукупність математичних співвідношень, рівнянь, нерівностей, що описують основні закономірності, властиві досліджуваному процесу, об'єкту або системі.

Математична модель є абстрактним відображенням реального процесу (явища) і в міру своєї абстрактності може його характеризувати більш-менш точно. Загальний зміст математичної моделі: Необхідно знайти множину змін Х1, Х2…Хn Xj(j=1,n) при яких задана цільова функція приймає екстремальне значення: 1)F=f(Xj) ext(max,min), при виконанні обмежень виробничого характеру.

2) ; 3)при зміні величини або численні. Для задач оптимізації розроблені моделі та алгоритми розв’язання, які класифікуються згідно з поведінкою цільової функції та обмеження моделі.

28. Постановка завдання оптимального виробничого планування. Математична модель.

Для виготовлення n видів продукції P1, ..., Pn використовується m видів сировини S1, ..., Sm, запаси якого обмежені і становлять відповідно b1, ..., bm одиниць. Відомо, що на виробництво одиниці продукції P_j (j= ) витрачається аij одиниць ресурсу Si (i= ,, а прибуток від реалізації одиниці продукції P_j (j= становить с_j (j= .Потрібно визначити план виробництва, який дозволяє при наявних ресурсах отримати максимальний прибуток підприємства від реалізації продукції. Математична модель завдання оптимального виробничого планування:

29. Завдання про суміші. Постановка і математична модель.

Задача визначення оптимального складу суміші виникає тоді, коли з наявних видів сировини шляхом їх змішування необхідно отримати кінцевий продукт із заданими властивості-ми. До цієї групи завдань відносяться, наприклад, задачі одержання сумішей для різних марок бензину в нафтопереробній промисловості, сумішей для отримання бетону в будівництві, завдання про вибір дієти, складання кормового раціону в тваринництві. При цьому потрібно, щоб вартість такої суміші була мінімальною.

Змістова постановка цієї задачі така: необхідно виробляти кінцевий продукт, який складається з n матеріалів. Кожний j-й кінцевий матеріал виготовляється із m типів ресурсів. Оціночні коефіцієнти для виробництва одиниць кожного j-го матер. Задано величинами Cj. По кожному i-му вихідному ресурсу задано обсяги bi та нормативні коефіцієнти aij. Необхідно скласти матем.модель, яка передбачає екстремальне значення цільової функції при виробництві кінцевого продукту. Позначимо через хj-обсяги матер. Кінцевого прод., тоді матем модель має вигляд: 1. цільова функція 2. обмеження 3.